Electromagnetic Theory: Unit I: (b) Coulombs Law and Electric Field Intensity
Electric Field Intensity
Statement, Definition, Formula, Steps to Solve Problems, Example Problems
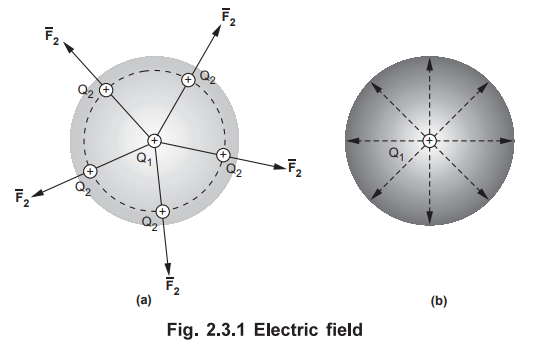
• If any other similar charge Q2 is brought near it, Q2 experiences a force. Infact if Q2 is moved around Q1, still Q2 experiences a force as shown in the Fig. 2.3.1 (a).
Electric Field Intensity
AU : May-06,07,10,12,15,16,19,
Dec.-03,09,12,17,18
•
Consider a point charge Q1 as shown in Fig. 2.3.1 (a).
•
If any other similar charge Q2 is brought near it, Q2
experiences a force. Infact if Q2 is moved around Q1,
still Q2 experiences a force as shown in the Fig. 2.3.1 (a).
•
Thus there exists a region around a charge in which it exerts a force on any
other charge. This region where a particular charge exerts a force on any other
charge located in that region is called electric
field of that charge. The electric field of Q1 is shown in the
Fig. 2.3.1 (b).
•
The force experienced by the charge Q2 due to Q1 is given
by Coulomb's law as,

•
Thus force per unit charge can be written as,

•
This force exerted per unit charge is called electric field intensity or electric
field strength. It is a vector quantity and is directed along a segment
from the charge Q1 to the position of any other charge. It is
denoted as ![]() .
.
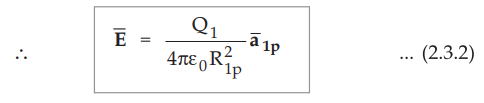
where
p = Position of any other charge around Q1
•
The equation (2.3.2) is the electric field intensity due to a single point
charge Q1 in a free space or vacuum.
•
Another definition of electric field intensity is the force experienced by a
unit positive test charge i.e. Q2 = 1C
•
Consider a charge Q1 as shown in the Fig. 2.3.2. The unit positive
charge Q2 = 1 C is placed at a distance R from Q1. Then
the force acting on Q2 due to Q1 is along the unit vector ![]() . As the charge Q2 is unit
charge, the force exerted on Q2 is nothing but electric field
intensity
. As the charge Q2 is unit
charge, the force exerted on Q2 is nothing but electric field
intensity ![]() of Q1 at the point where unit charge is
placed.
of Q1 at the point where unit charge is
placed.

•
If a charge Q1 is located at the center of the spherical co-ordinate
system then unit vector ![]() in the equation (2.3.3) becomes the radial
unit vector
in the equation (2.3.3) becomes the radial
unit vector ![]() coming radially outwards from Q1. And the
distance R is the radius of the sphere r.
coming radially outwards from Q1. And the
distance R is the radius of the sphere r.
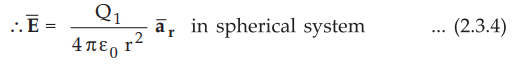
1. Units of 
•
The definition of electric field intensity is,
![]() = Force/Unite Charge = (N) Newtons/(C) Coulomb
= Force/Unite Charge = (N) Newtons/(C) Coulomb
•
Hence units of ![]() is N/C. But the electric potential has units J/C i.e.
Nm/C and hence
is N/C. But the electric potential has units J/C i.e.
Nm/C and hence ![]() is also measured in units V/m (volts per metre). This unit is used practically to express
is also measured in units V/m (volts per metre). This unit is used practically to express ![]() .
.
2. Method of Obtaining E in Cartesian System
•
Consider a charge Qi located at point A(x1,y1,z1)
as shown in the Fig. 2.3.3. It is required to obtain ![]() at any point B (x, y, z)
in the cartesian system. Then
at any point B (x, y, z)
in the cartesian system. Then ![]() at point B can be obtained using
following steps :
at point B can be obtained using
following steps :

Step 1 : Obtain
the position vectors of points A and B.

•
Substituting  interms of the cartesian co-ordinates of A and
B, the required electric field intensity
interms of the cartesian co-ordinates of A and
B, the required electric field intensity ![]() at the point B can be
obtained.
at the point B can be
obtained.
3. Electric Field due to Discrete Charges
•
Similar to a force exerted on a charge due to n number of charges is the vector
sum of the individual force exerted by each charge, the electric field at a
point due to n number of charges is to be obtained using law of superposition.
•
Consider n charges Q1,Q2 ...Qn as shown in the
Fig. 2.3.4. The combined electric field intensity is to be obtained at point P.
The distances of point P from Q1,Q2 ...Qn are
R1,R2,...Rn respectively. The unit vectors
along these directions are a  respectively.
respectively.

•
Then the total electric field intensity at point P is the vector sum of the
individual field intensities produced by the various charges at the point P.
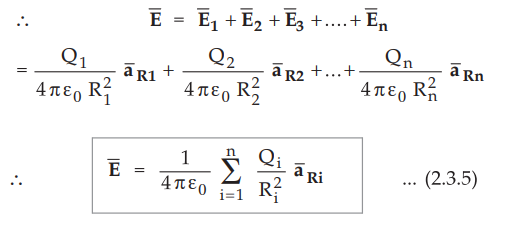
•
Each unit vector can be obtained by using the method discussed earlier.

4. Important Observations
•
The important observations related to ![]() are,
are,
1. ![]() around a charge Q1 is directly proportional to the
charge Q1.
around a charge Q1 is directly proportional to the
charge Q1.
2. ![]() around a charge Q1 is inversely proportional to the
distance between charge Q1 and point at which
around a charge Q1 is inversely proportional to the
distance between charge Q1 and point at which ![]() is to
be calculated. More is the distance less is the electric field intensity and
less will be the force experience by a unit charge placed at that point.
is to
be calculated. More is the distance less is the electric field intensity and
less will be the force experience by a unit charge placed at that point.
3.
The field intensity ![]() at any point and force
at any point and force ![]() exerted on a charge
placed at the same point are always in the same direction.
exerted on a charge
placed at the same point are always in the same direction.
4.
Placing unit charge is a method of detecting the presence of electric field
around a charge. Without any unit test charge placed nearby, every charge has
its electric field always existing, around it.
5.
The test charge placed must be small enough so that the electric field
intensity ![]() to be measured should not get disturbed.
to be measured should not get disturbed.
Ex. 2.3.1
A charge of - 0.3 ,µC is located at A(25,
- 30, 25) (in cm) and a second charge of 0.5µC is at B (-10, 8,12) cm. Find the
electric field intensity at the origin. AU : May-10, Dec.-03, 17, Marks 4
Sol. :
A (0.25, - 0.3, 0.15) m, - 0.3 µC
B
(- 0.1, 0.08, 0.12) m, 0.5 µC
O
(0, 0, 0)

Ex. 2.3.2
Consider a square of side 5 cm. Three
positive charges of 100 nC each are located at three comers of the square. Find
the value of the electric field intensity at the fourth corner of the square.AU : May-12, Marks 8
Sol. :
The arrangement is shown in the Fig. 2.3.6. Let the charges are placed at A, B
and C while ![]() is to be obtained at fourth comer O.
is to be obtained at fourth comer O.

Ex. 2.3.3
Point charges 5 nC and - 2 nC are located
at (2, 0, 4) and (- 3, 0, 5), respectively. 1) Determine the force on a 1 nC
point charge located at (1, - 3, 7), 2) Find the electric field intensity at
(1, - 3, 7)AU: Dec.-12,18, Marks 8
Sol :
The arrangement is shown in the Fig. 2.3.7.

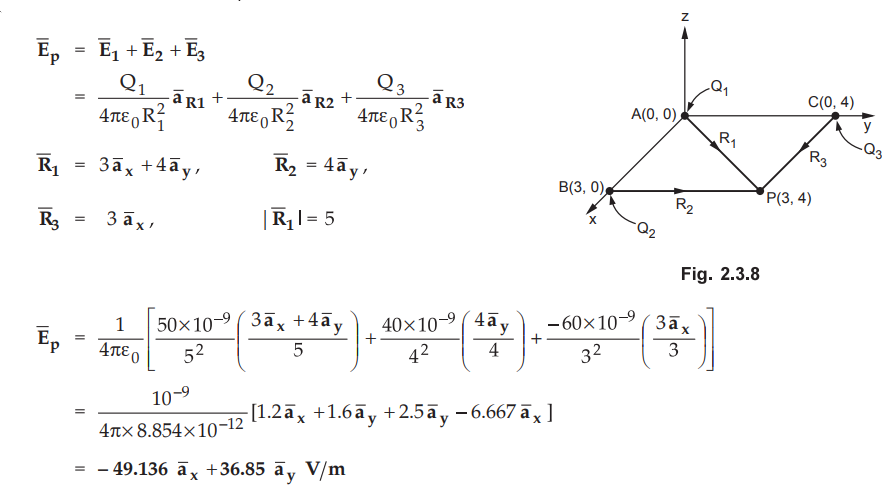
Ex.
2.3.4 Three point charges in free space are located as fllows 50 nC at (0,0) m;
40 nC at (3,0) m; = 60 nC at (0,4) m. Find the electric field intensity at
(3,4) m.
Sol
:
The charges are shown in the Fig. 2.3.8.
Ex. 2.3.5 A positive point charge 100 × 10-12
C is located in air at x = 0, y = 0.1 m and another such charge at x = 0,
y = -.01 m. What is the magnitude and direction of E at x = 0.2 m , y = 0.m AU:
May-15, Marks 6
So. :
The charges are shown in the Fig. 2.3.9

Ex. 2.3.6
A charge of 1 C is at (2, 0, 0). What
charge must be placed at (- 2, 0, 0) which will make y component of total ![]() zero at the point (1, 2, 2) ? AU :
Hay-19, Marks 13
zero at the point (1, 2, 2) ? AU :
Hay-19, Marks 13
Sol. :
The various points and charges are shown in the Fig. 2.3.10.
The
position vectors of points A, B and P are,

This
is the required charge Q2 to be placed at (-2,0,0) which will make y
component of ![]() zero at point P.
zero at point P.
Examples for Practice
Ex. 2.3.7 Determine electric field ![]() at the origin due to a point charge of 54.9 nC located at (- 4, 5, 3) m in
cartesian co-ordinates.
at the origin due to a point charge of 54.9 nC located at (- 4, 5, 3) m in
cartesian co-ordinates.

Ex. 2.3.8 Calculate ![]() at P(l, 1, 1) in
free space caused by four identical 3 nC point charges located at P1
= (1, 1, 0), P2 = (-1, 1, 0), P3 = (-1, -1, 0) and P4
= (1, -1, 0).
at P(l, 1, 1) in
free space caused by four identical 3 nC point charges located at P1
= (1, 1, 0), P2 = (-1, 1, 0), P3 = (-1, -1, 0) and P4
= (1, -1, 0).
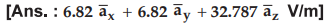
Ex. 2.3.9 A
charge Q1 = - 10 nC is at the origin in free space. If the
x-component of E is to be zero, at the point (3, 1, 1), what charge Qt
should be kept at the point (2, 0, 0) ? [Ans.: 4.2728 nC]
Review Questions
1. Define electric field intensity and explain the procedure to obtain electric field at a point due to number of discrete charges.
AU : May-07, Dec.-09, Marks 8
2. Derive electric field intensity at a point in a field due to a point charge.
AU : May-06, Marks 6
Electromagnetic Theory: Unit I: (b) Coulombs Law and Electric Field Intensity : Tag: : Statement, Definition, Formula, Steps to Solve Problems, Example Problems - Electric Field Intensity
Related Topics
Related Subjects
Electromagnetic Theory
EE3301 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
