Full Wave Rectifier

 Full Wave Rectifier

AU : Dec.-O9, 10, 11, 13, May-15, 17

• The full wave rectifier conducts during both positive and negative half cycles of input a.c. supply. In order to rectify both the half cycles of a.c. input, two diodes are used in this circuit. The diodes feed a common load R_L with the help of a centre tap transformer. The a.c. voltage is applied through a suitable power transformer with proper turns ratio.

• The full wave rectifier circuit is shown in the Fig. 1.16.1.

• For the proper operation of the circuit, a centre-tap on the secondary winding of the transformer is essential.

 

1. Operation of the Circuit

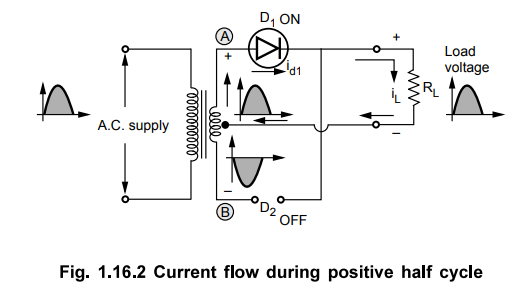
• Consider the positive half cycle of a.c. input voltage in which terminal (A) is positive and terminal (B) negative. The diode D1 will be forward biased and hence will conduct; while diode D2 will be reverse biased and will act as an open circuit and will not conduct. This is illustrated in the Fig. 1.16.2.

• The diode D₁ supplies the load current, i.e. iL = idl. This current is flowing through upper half of secondary winding while the lower half of secondary winding of the transformer carries no current since diode D₂ is reverse biased and acts as an open circuit.

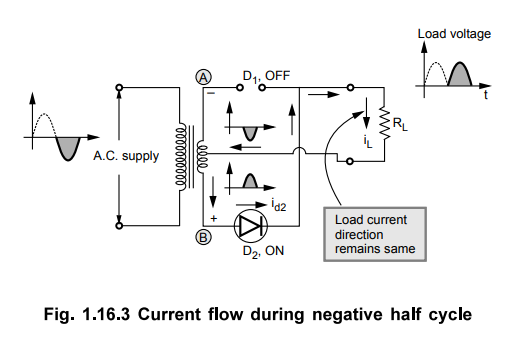
• In the next half cycle of a.c. voltage, polarity reverses and terminal (A) becomes negative and (B) positive. The diode D₂ conducts, being forward biased, while D₁ does not, being reverse biased. This is shown in the Fig. 1.16.3.

• The diode D₂ supplies the load current, i.e. iL = id₂ . Now the lower half of the secondary winding carries the current but the upper half does not.

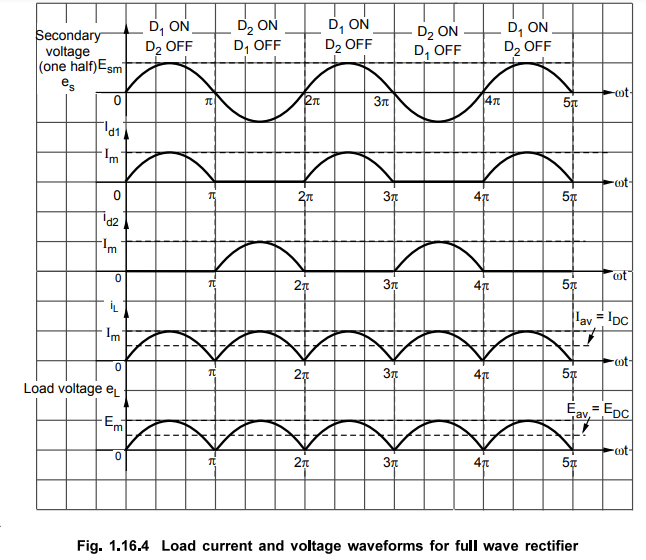
• It is noted that the load current flows in both the half cycles of a.c. voltage and in the same direction through the load resistance. Hence we get rectified output across the load. The load current is sum of individual diode currents flowing in corresponding half cycles. It is also noted that the two diodes do not conduct simultaneously but in alternate half cycles. The individual diode currents and the load current are shown in the Fig. 1.16.4.

• Thus the full wave rectifier circuit essentially consists of two half wave rectifier circuits working independently (working in alternate half cycles of a.c.) of each other but feeding a common load. The output load current is still pulsating d.c. and not pure d.c.

 

2. Maximum Load Current

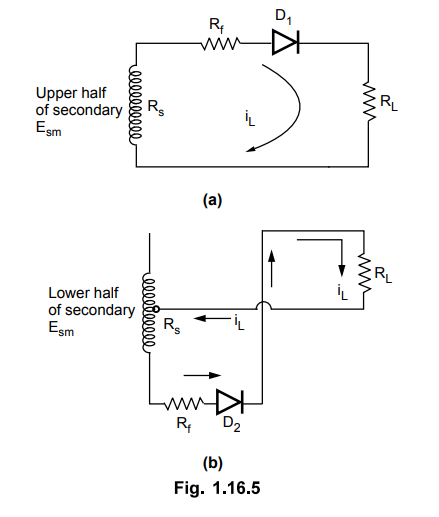
• Let R_f = Forward resistance of diodes, R_s = Winding resistance of each half of secondary

• R_L = Load resistance, e_g = Instantaneous a.c. voltage across each half of secondary

e_m = E_sm sin ωt    where ω = 2πf

E_sm = Maximum value of a.c. input voltage across each half of secondary winding.

• Hence we can write the expression for the maximum value of the load current, looking at equivalent circuit shown in the Fig 1.16.5.

 

3. Average D.C. Load Current (l_DC)

• Consider one cycle of the load current iL from 0 to - to obtain the average value which is d.c. value of load current.

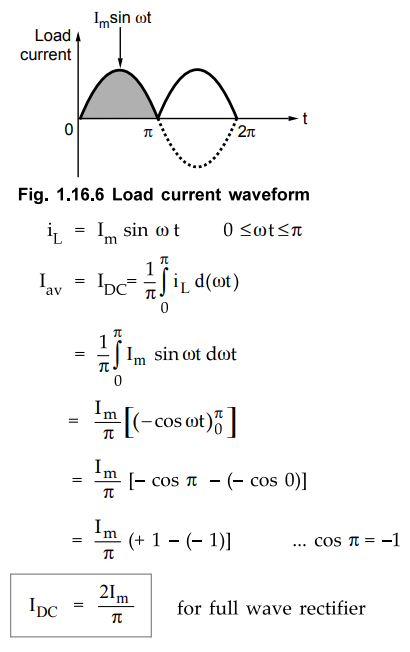
• For half wave it is I /n and full wave rectifier is the combination of two half wave circuits acting alternately in two half cycles of input. Hence obviously the d.c. value for full wave circuit is 2 I_m/π

 

4. Average D.C. Load Voltage (E_DC)

• The d.c. load voltage is,

 

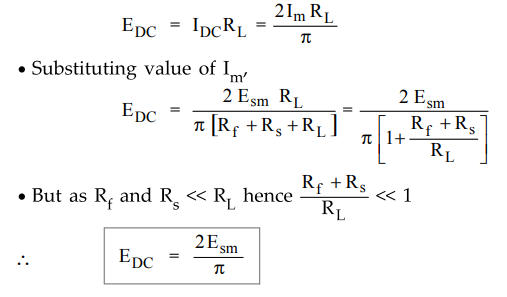
5. RMS Load Current (I_RMS)

• The R.M.S. value of current can be obtained as follows :

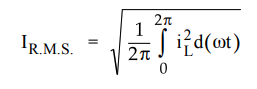
• Since two half wave rectifier are similar in operation we can write,

 

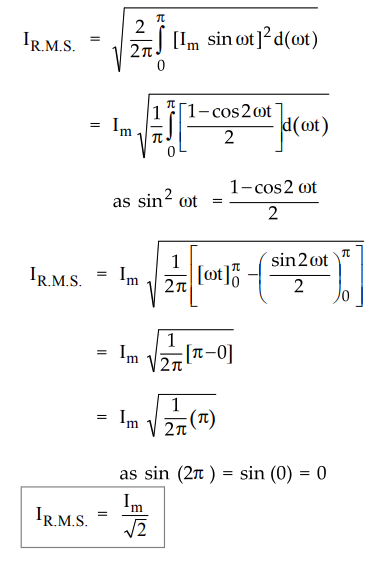
6. R.M.S. Value of the Load Voltage

As the load is resistive, the r.m.s. value of the load voltage is given by,

 

7. D.C. Power Output (P_DC)

Key Point : Instead of remembering this formula, students can use the expression E_DCI_DC or I²_DCR_L to calculate P_DC while solving the problems.

 

8. A.C. Power Input (P_AC)

• The a.c. power input is given by,

 

9. Rectifier Efficiency (η)

 

10. Ripple Factor (ɤ)

• As derived earlier in case of half wave rectifier the ripple factor is given by a general expression,

 

Key Point : This indicates that the ripple contents in the output are 48 % of the d.c. component which is much less than that for the half wave circuit.

 

11. Load Current (I_L)

• The Fourier for the load current is obtained by taking the sum of the series for the individual rectifier current. The two diodes conduct in alternate half cycles, i.e. there is a phase difference of π radians between two diode currents, Hence,

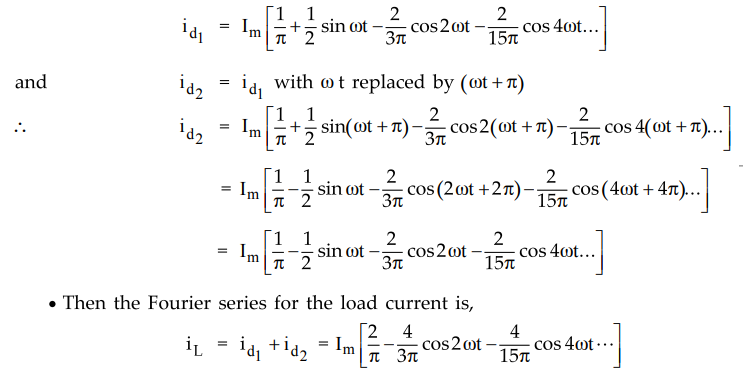
• The first term in the above series represents the average or d.c. value, while the remaining terms "ripple". It is seen that the lowest frequency of the ripple is 2f, i.e. twice the supply frequency of a.c. supply. The lowest ripple frequency in the load current of the full-wave connection, is double than that in the half-wave connection.

• As seen from the Fig. 1.16.2 and Fig. 1.16.3 the individual diode currents are flowing in opposite directions through the two halves of the secondary winding. Hence the net secondary current will be difference of individual diode currents.

Thus, i_sec = id₁ - id₂

• The Fourier series of i_sec is obtained by the difference between the series of individual diode currents. Using above relations we can write,

i_sec = I_m  sin ω t

• Hence under ideal conditions, the secondary current is purely sinusoidal. No d.c. component flows through the secondary hence there is no danger of saturation. This reduces the transformer losses and overall size and cost of the circuit. Thus the transformer gets utilised effectively.

 

12. Peak Inverse Voltage (PIV)

• It can be observed from the circuit diagram that when the diode is reversed biased then full transformer secondary voltage gets impressed across it. The drop across conducting diode is assumed zero. Thus the peak value of the inverse voltage to which diode gets subjected is voltage across both the parts of the transformer secondary. This is shown in the Fig. 1.16.7.

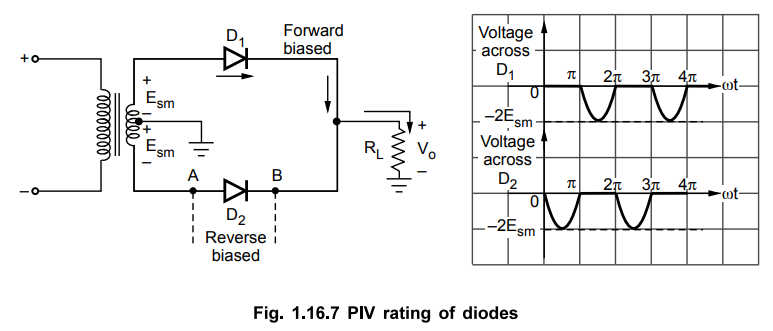
• It can be seen that when D₂ is reverse biased, point A is at – E_sm with respect to ground while point B is at + Esm with respect to ground, neglecting diode drop. Thus total peak voltage across D₂ is 2E_sm

PIV of diode = 2 E_sm = π E_DC|I_DC = 0

• where Esm = Maximum value of a.c. voltage across half the secondary of transformer. If the diode drop is considered to be 0.7 V then the PIV of reverse biased diode is,

PIV of diode = 2E_sm - 0.7

This is because only one diode conducts at a time.

 

13. Transformer Utilization Factor (T.U.F.)

• In full wave rectifier, the secondary current flows through each half separately in every half cycle. While the primary of transformer carries current continuously. Hence T.U.F. is calculated for primary and secondary windings separately and then the average T.U.F. is determined.

The primary of the transformer is feeding two half-wave rectifiers separately. These two half-wave rectifiers work independently of each other but feed a common load. We have already derived the T.U.F. for half wave circuit to be equal to 0.287. Hence,

T.U.F. for primary winding = 2 × T.U.F. of half wave circuit

= 2 × 0.287 = 0.574

The average T.U.F for fullwave circuit will be

AVerageT . U . F . for full wave rectifier circuit =          T . U . F . of primary + T . U . F . of secondary / 2

0.574 + 0.812 / 2 = 0.693

Average T.U.F. for full-wave rectifier = 0.693

Key Point: Thus in full wave circuit transformer gets utilized more than the half wave rectifier circuit.

 

14. Voltage Regulation      

For a full wave circuit,

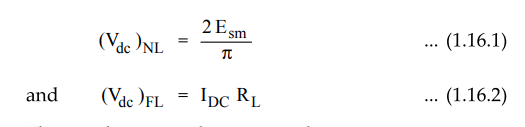
The regulation can be expressed as,

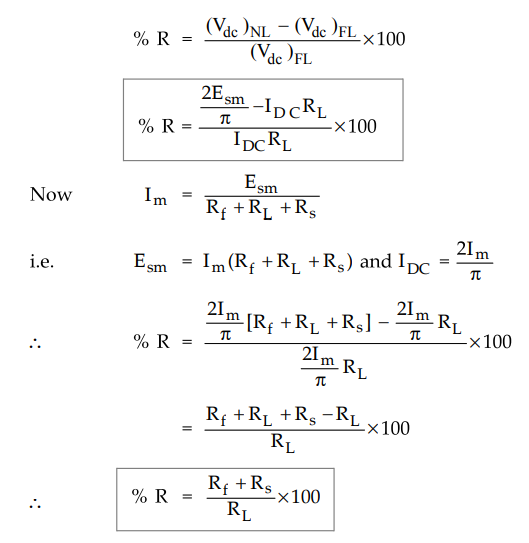
• Neglecting winding resistance Rs, the regulation can be expressed as,

% R ≈ R_f / R_L × 100

where R_f = Forward resistance of the diode.

• The regulation characteristics is drooping, as discussed earlier in case of half wave rectifier as output voltage decreases as load increases from no load to full load.

 

15. Advantages of Full Wave Rectifier

1. The d.c. load voltage and current are more than half wave.

2. No d.c. current through transformer windings hence no possibility of saturation.

3. T.U.F. is better as transformer losses are less.

4. The efficiency is higher.

5. The large d.c. power output.

6. The ripple factor is less.

 

16. Disadvantages of Full Wave Rectifier

1. The PIV rating of diode is higher.

2. Higher PIV diodes are larger in size and costlier.

3. The cost of centre tap transformer is higher.

 

17. comparison of Full Wave and Half Wave Circuit

• For comparison, we assume that the full-wave and half-wave circuits use identical diodes, identical load resistances and the voltage across half the secondary winding of transformer used in full-wave circuit is the same as the voltage across the secondary winding of the transformer used in half-wave circuit.

1. The d.c. load current in case of full wave circuit is twice to that in half wave circuit; similarly the d.c. load voltage in full wave circuit is twice that in half wave circuit.

2. The lowest ripple frequency in full wave circuit is twice that in half wave circuit. Now to remove ripple, the additional circuits called filter circuits are used along with rectifier circuits. But as the frequency is more in full-wave, the capacitor values required in capacitance filter are much less hence smaller elements are sufficient in filter circuits used with full wave circuit to reduce ripple.

3. Because there is no net d.c. current through windings of the transformer used in full wave circuit, the losses are less as compared to losses in transformer used in half wave circuit.

4. The full wave connection gives d.c. power output four times as large, when compared with half wave connection.

5. The efficiency of rectification in a full wave connection is twice that for half wave connection.

6. The ripple factor is less for full-wave, i.e. rectification is more nearly complete for full wave as compared to half-wave.

 

Ex. 1.16.1 If the required D.C. output voltage is 9 V, assuming ideal diodes, calculate the A.C. r.m.s. input voltage required in the following cases :

i) Half wave rectifier, ii) Centre-tapped full wave rectifier.

Sol. : E_DC = 9 V, Ideal diodes

i) Half wave rectifier :

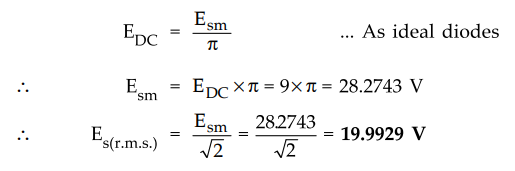
• This is required a.c. r.m.s. input voltage on secondary of transformer.

ii) Centre-tapped full wave rectifier :

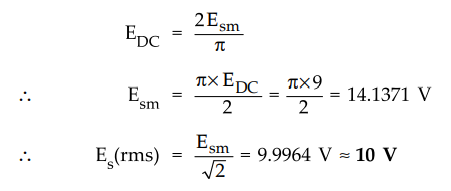
• This is required a.c. r.m.s voltage on input side from either end of secondary to center tap.

• Thus the transformer secondary rating must be 10 V - 0 - 10 V.

 

Ex. 1.16.2 A full-wave rectifier circuit is fed from a transformer having a centre-tapped secondary winding. The rms voltage from either and of secondary to center tap is 30 V. If the diode forward resistance is 2 Ω and that of the half secondary is 8 Ω, for a load of 1 k Ω, calculate, a) Power delivered to load , b) % Regulation at full load, c) Efficiency of recitification, d) T..U.F. of secondary.

Sol : Given

Review Questions

1. Explain the operation of FWR with centre tap transformer with neat circuit diagram. Also derive the following for this rectifier : i) dc output voltage ii) dc output current iii) RMS output voltage iv) Ripple factor v) Peak inverse voltage

AU : Dec.-09,10,ll, Marks 16; Dec.-13, Marks 8

2. Derive the expressions for the following parameters of the full wave rectifier.

a) Average d.c. current (I_DC)

b) Average d.c. output voltage (E_DC)

c) R.M.S. value of current (I_RMS)

d) D.C. power output (P_DC)

e) A.C. power input (P_AC)

f) Rectifier efficiency (η).

3. Prove that the ripple factor for the full-wave rectifier circuit is 0.48.

4. Compare the full wave rectifier with half-wave rectifier circuit. 

5. Derive the expression for maximum efficiency of a full wave rectifier.

6. A full-wave rectifier circuit is fed from a transformer having a centre-tapped secondary winding. The r.m.s. voltage from either end of secondary to center tap is 20 V. If the diode forward resistance is 3 Ω and that of the half secondary is 5 Ω, for a load of 1 hΩ, calculate

a) Power delivered to load, b) % Regulation at full load, c) Efficiency at full load, d) T.U.F. of secondary.

(Ans.: a) P_dc = 0.3191 W, b) % Regulation = 0.7469 %, c) Efficiency of full load = 0.8041, d) T.U.F. = 0.804)

7. Explain the action of a full-wave rectifier using diodes and give waveforms of input and output voltages.

AU : May-15, Marks 8