(ii) Continuous random variables

CONTINUOUS RANDOM VARIABLES

(i) Definition: Continuous Random Variable

A random variable X is said to be continuous if it takes all possible values between certain limits say from real number 'a' to real number 'b'.

Example: The length of time during which a vacuum tube installed in a circuit functions is a continuous random variable.

Note: If X is a continuous random variable for any x₁ and x₂ P(x1 ≤ X ≤ x₂) P(x₁ <X ≤ x₂) = P(x₁ ≤ X < x₂) = P(x₁ < X < x₂)

(ii) Probability density function :

For a continous random variable X, a probability density function is a function such that

(1) f(x) ≥ 0

(2) 

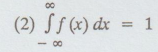
(3) P(a ≤ X ≤ b) = 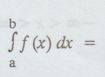 f (x) dx = area under f (x) from a to b for any

a and b.

Note: A probability density function is zero for the values of X which do not occur and it is assumed to be zero wherever it is not specifically defined.

(iii) Cumulative distribution function

The cumulative distribution function of a continuous random variable X is

 

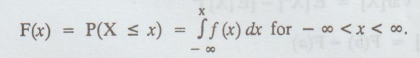
Note: The probability density function of a continuous random variable can be determined from the cumulative distribution function by differentiating.

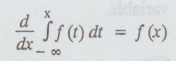 [ fundamental theorem of calculus]

f(x) = d/dxF[x] as long as the derivative exists.

 (iv) The mean or expected value of a continuous random variable X.

Suppose X is a continuous random variable with probability density function f(x). The mean or expected value of X, denoted as μ or E(X) is

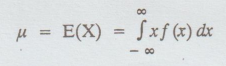
A useful identity is that for any function g,

 (v) The variance of a continuous random variable X.

The variance of X, denoted as V(X) or σ², is

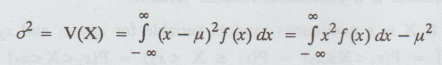
= E[X²] - [E (X)]²

Note: The standard deviation of X is σ = √Var (X).

(vi) FORMULA

6.Variance = Var[X] = E [X²] - [E [X]]²

7. P[a ≤  X ≤  b] = F(b) - F(a)

8. P(a ≤ X ≤ b) = P(a ≤ X < b) = P[ a < X ≤ b]

= P[a < X < b], X being a continuous random variable.

9. 0 ≤ F(x) ≤ 1

10. F(x) is a non-decreasing function of X.

i.e., if x₁ < x₂ then F(x₁) < F (x₂)

 

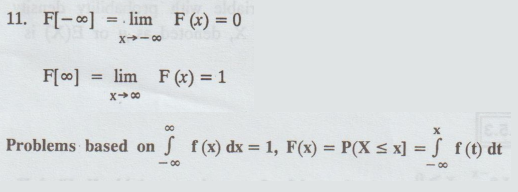
Example 1.5.1

A continuous random variable X has p.d.f. f (x) = k, 0 ≤ x ≤1. Determine the constant k. Find P(X ≤1/4].

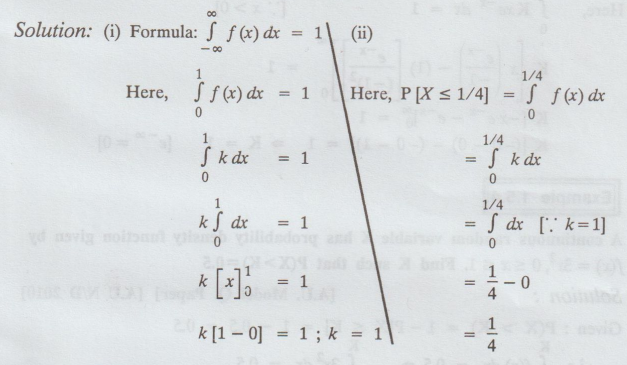
Example 1.5.2

Given that the p.d.f of a R.V. X is f(x) = Kx, 0 < x < 1, find K and P(X > 0.5) [A.U. Dec, 96]

 

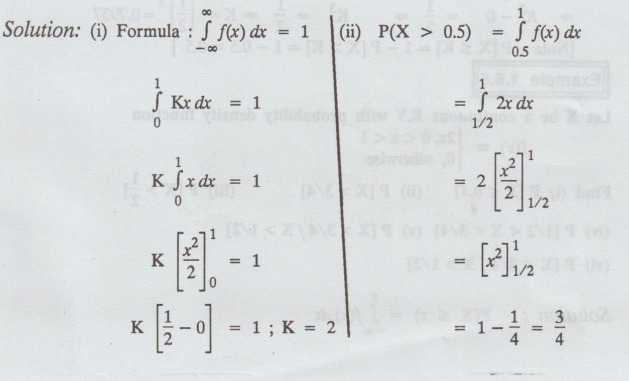
Example 1.5.3

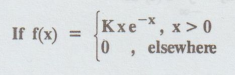is the p.d.f. of a random variable X. Find K. [A.U CBT M/J 2010]

Solution :

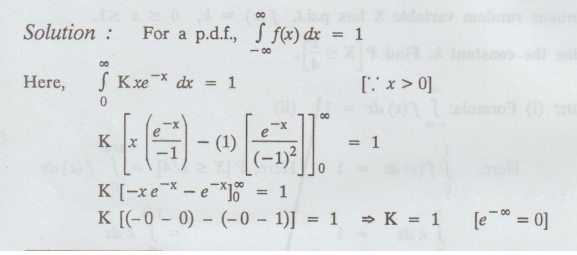
K [-x e^-x - e^-x]_o^∞ = 1

K [(- 0 - 0) - (0 - 1)] = 1 ⇒ K = 1 [ e^-∞ ₌ 0 ]

 

Example 1.5.4

A continuous random variable X has probability density function given by f(x) = 3x², 0 ≤  x  ≤ 1. Find K such that P(X > K) = 0.5

 [A.U. Model Q. Paper] [A.U N/D 2010]

Solution:

Given: P(X > K) = 1 - P[X ≤ K] = 1 - 0.5 = 0.5

 [Note: P[ X ≤ K] = 1 − P [X > K] = 1 - 0.5 = 0.5 ]

 

Example 1.5.5

Let X be a continuous R.V with probability density function

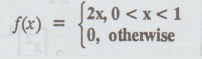
Find (i) P (X ≤ 0.4] (ii) P [X > 3/4] (iii) P [X > ½ ] (iv) P [1/2 < X < 3/4] (v) P [X > ¾ / X > 1/2] (vi) P[X < ¾ / X > 1/2]

Solution :

 

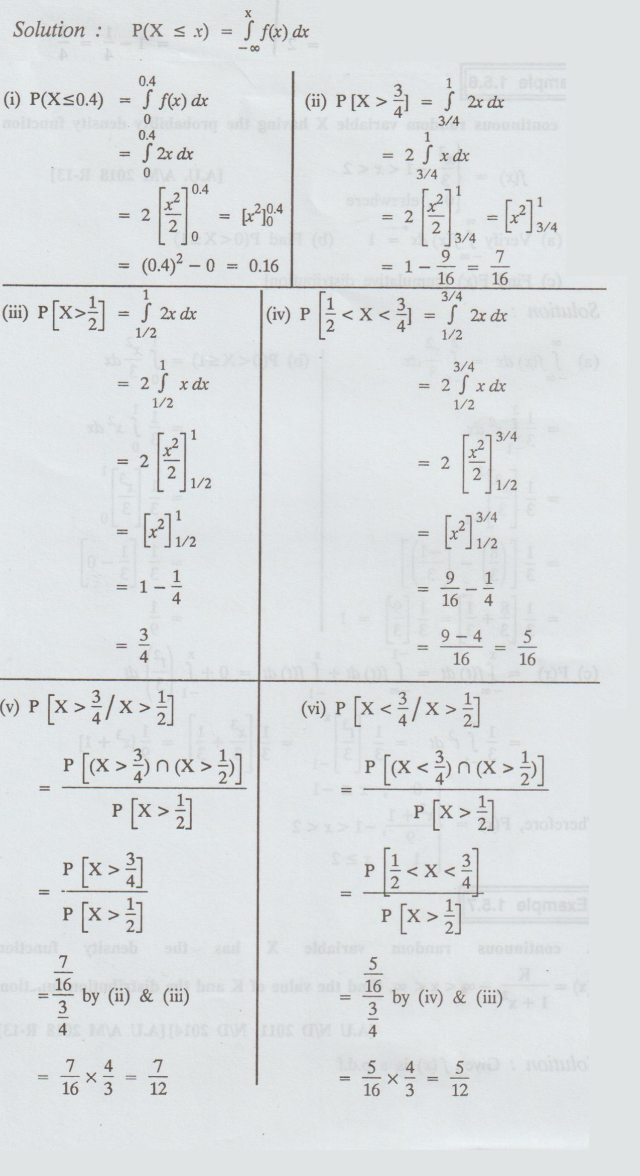
Example 1.5.6

In a continuous random variable X having the probability density function

(b) Find P(0 < X ≤ 1) (c) Find F(x) [cumulative distribution]

Solution:

 

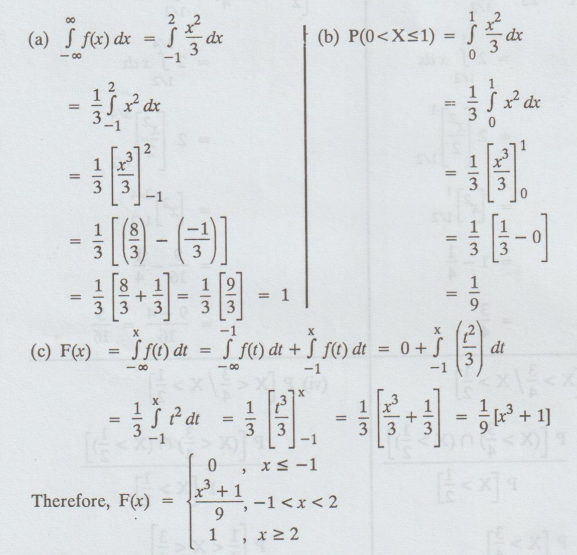
Example 1.5.7

A continuous random variable X has the density function f(x) = K / 1 + x^2' ∞ < x < ∞. Find the value of K and the distribution function.

[A.U N/D 2011, N/D 2014] [A.U A/M 2018 R-13]

Solution: Given f (x) is a p.d.f

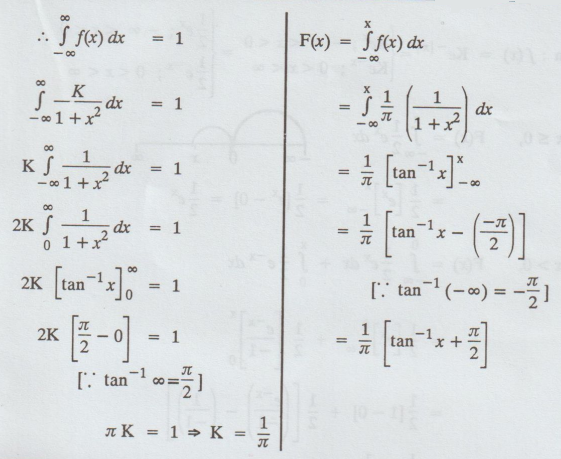
Example 1.5.8

The p.d.f. of a continuous R.V. X is f(x) = Ke^-x. Find K and the F[x].

[A.U. 2005] [A.U Trichy M/J 2011] [A.U A/M 2010]

Solution :

 

Example 1.5.9

A continuous random variable X that can assume any value between x = 2 and x = 5 has a density function given by f(x) = k(1 + x). Find P [X < 4] [A.U M/J 2006, M/J 2007, N/D 2011, N/D 2012] [A.U CBT N/D 2008, CBT Dec. 2009] [A.U A/M 2015, (RP) R13] [A.U A/M 2017 R8]

Solution :

 (i) Formula:

Example 1.5.10

A continuous random variable X has the distribution function

find K, probability density function f(x), P[X<2] [A.U. A/M. 2008]

Solution:

We know that,

P [X ≤ x]  = F[X]

 

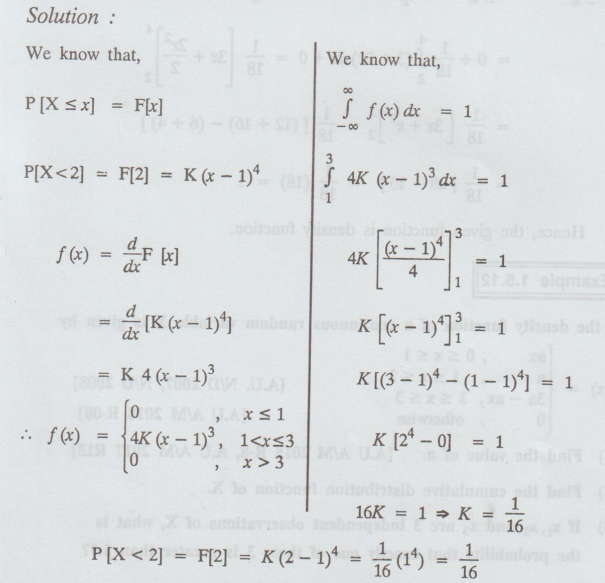
Example 1.5.11

Is the function defined as follows, a density function ? [A.U N/D 2006]

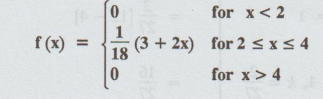
Solution: Condition for probability density function is

= 1/18 [28 – 10] = 1/18 (18) = 1

Hence, the given function is density function.

 

Example 1.5.12

If the density function of a continuous random variable X is given by

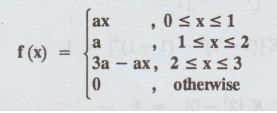
[A.U. N/D 2007, N/D 2008] [A.U A/M 2018 R-08]

(1) Find the value of a. [A.U A/M 2015 R-8, A.U A/M 2017 R13]

(2) Find the cumulative distribution function of X.

(3) If X₁, X₂ and X₃ are 3 independent observations of X, what is the probability that exactly one of these 3 is greater than 1.5?

Solution: (1) Since, f (x) is a p.d.f, then

Choosing an X and observing its value can be considered as a trial and X 1.5 can be considered as a success.

i.e., p = P[X > 1.5] = 1/2

p = ½ , q = ½ [ 1 = 1 – p]

As we choose 3 independent observation of X, n = 3.

By Bernoulli's theorem. [ P(x) = n C_{x P}^xq^n-x]

P(exactly one value > 1.5)

= P(1 success) = 3C₁ (1/2)¹ (1/2)^3-1

= 3 (1/2) (1/2)² = 3/8

 

Example 1.5.13

Experience has shown that while walking in a certain park, the time X (in mins.), between seeing two people smoking has a density function of the form

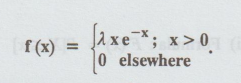[A.U. N/D 2007]

 (1) Calculate the value of λ.

(2) Find the distribution function of X.

 (3) What is the probability that Jeff, who has just seen a person smoking, will see another person smoking in 2 to 5 minutes? In atleast 7 minutes?

Solution:

Example 1.5.14

The diameter of an electric cable X is a continuous r.v. with pdf f(x) = kx (1-x), 0 ≤ x ≤1  [A.U N/D 2017 R-08]

(i) Find the value of k

(ii) c.d.f of X

 (iii) the value of a such that P (X < a) = P(X > a)

(iv) P (X ≤ 1/2 / 1/3 < X < 2/3 ]

Solution :

 

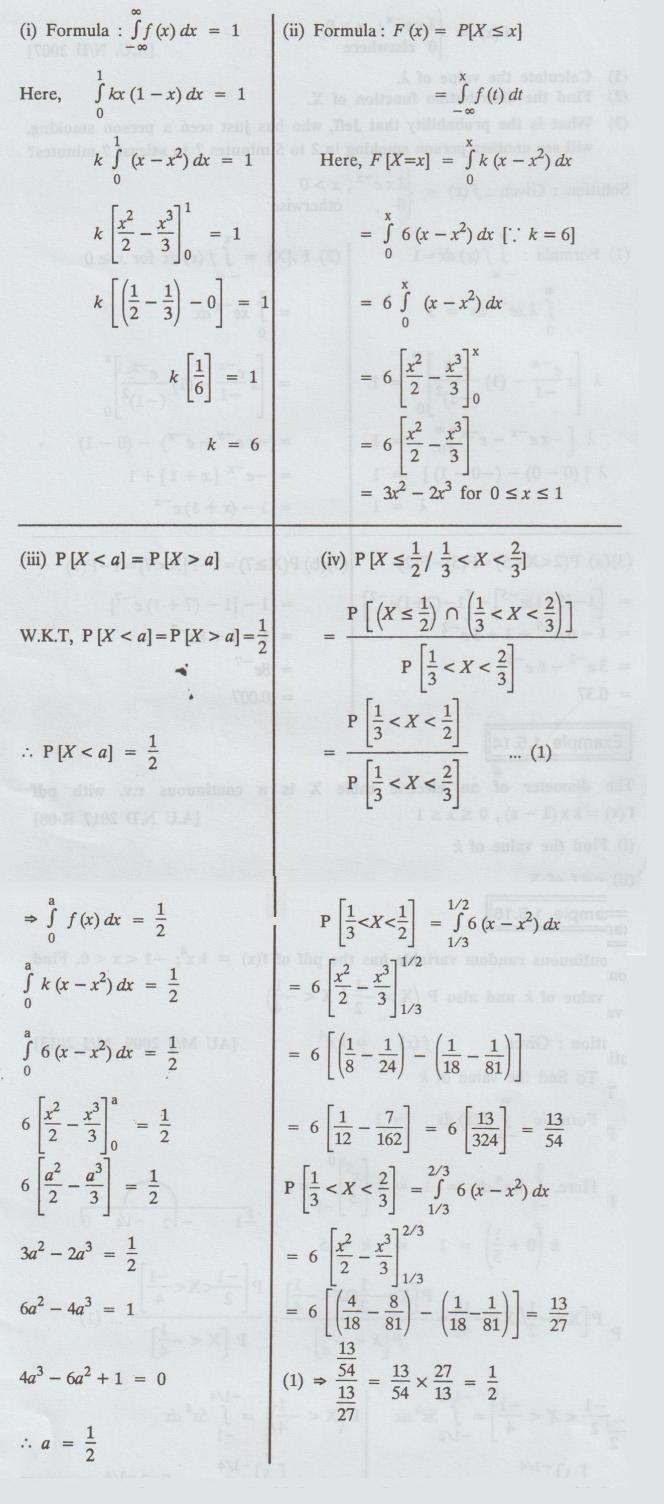
Example 1.5.15

A continuous random variable X that can assume values between x = 2 and x = 5 has dF = [2 (1 + x)/27] dx, find P (3 < X < 4)

Solution: We know that, f (x) = dF/ dx = 2 (1 + x ) 27/27 ,  2 ≤ x ≤ 5

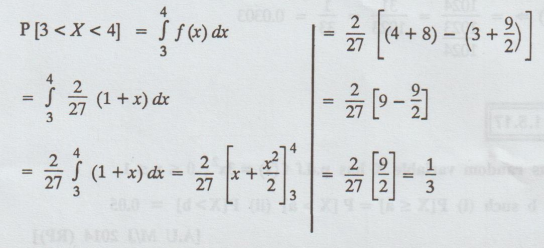
Example 1.5.16

A continuous random variable has the pdf of f(x) = kx⁴; -1 < x <0. Find the value of k and also P (x > -1/2 / X < -1/4) [AU M/J 2009, M/J 2013]

Solution: Given: f(x) = kx⁴

 (i) To find the value of k

(1) ⇒ = 31/1024 / 1023/1024 = 31/1023 = 1/33 = 0.0303

 

Example 1.5.17

A continuous random variable X has p.d.f f(x) = 3x², 0 ≤ x ≤1. Find a and b such (i) P[X ≤ a] = P [X> a] (ii) P[X>b] = 0.05 [A.U M/J 2014 (RP)]

Solution :

Problems based on f (x) = d/dx F [x], mean, variance

 

Example 1.5.18

The cumulative distribution function (cdf) of a random variable X is F(x) = 1- (1+ x)e^-x, x>0. Find the probability density function of X, Mean and variance of X. [AU M/J 2006, AU N/D 2010] [A.U A/M 2015 R8] [A.U A/M 2019 (R17) PS]

Solution: Given: F(x) = 1- (1+x)e^-x, x > 0

= 1-e^-x- xe^-x , x>0

p.d.f, f(x) = d/dx [F(x)] = d/dx [1-e^-x-xe^-x]

= 0+ e^-x - [x (-e^-x) + e^-x (1)]

= e^-x + xe^-x –e^-x

= xe^-x, x>0

= ( 0 – 0 + 0 – 0 ) – ( 0 - 0 + 0 – 6 )

= 6

Var(X) = E(X²) - [E (X)]² = 6 - (2)² = 6 - 4 = 2

 

Example 1.5.19

The sales of a convenience store on a randomly selected day are X thousand dollars, where X is a random variable with a distribution function of the following form :

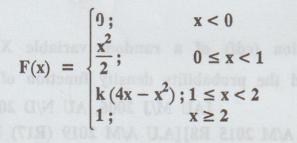
 [A.U. N/D 2007]

Suppose that this convenience store's total sales on any given day are less than $ 2000.

(1) Find the value of k.

(2) Let A and B be the events that tomorrow the store's total sales are between 500 and 1500 dollars, and over 1000 dollars, respectively. Find P(A) and P(B).

(3) Are A and B independent events?

Solution :

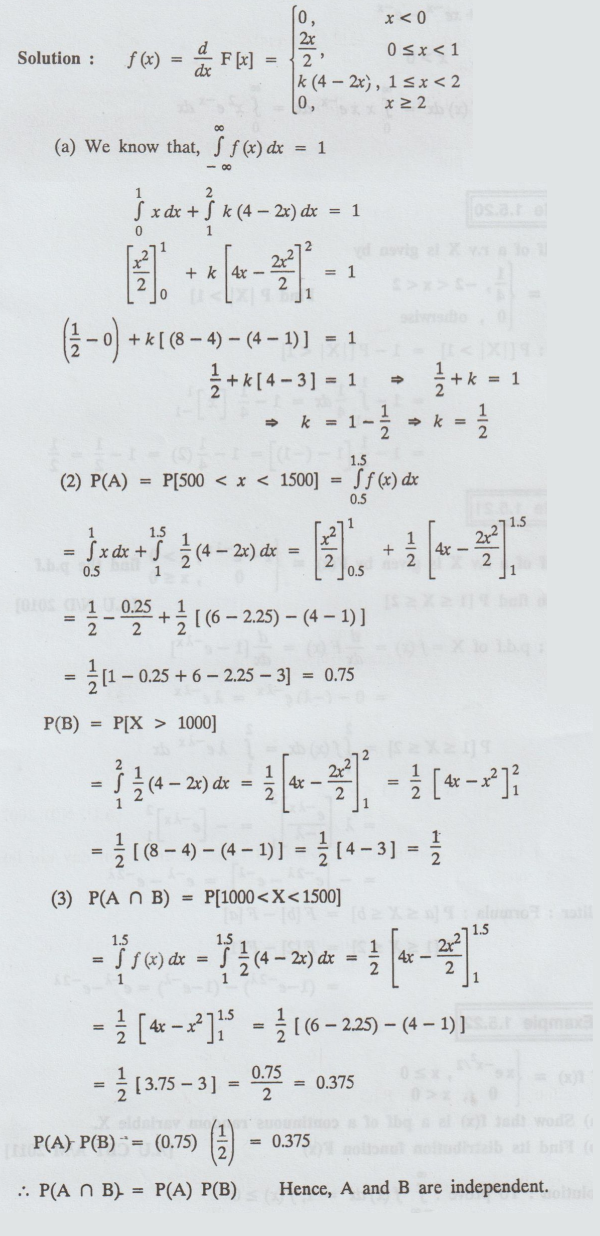
P(A ∩ B) = P(A) P(B) Hence, A and B are independent.

 

Example 1.5.20

If the pdf of a r.v X is given by

 

Example 1.5.21

If the cdf of a r.v X is given by F(x) = 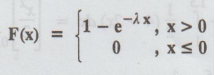 of X, also find P [1 ≤ X ≤ 2] [A.U N/D 2010]

Solution : p.d.f of X = ƒ (x) = d/dx F(x) = d/dx [1 – e^-λx]

 

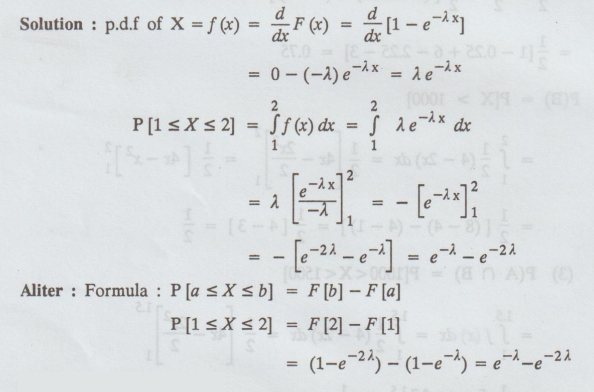
Example 1.5.22

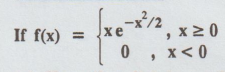
 (a) Show that f(x) is a pdf of a continuous random variable X.

(b) Find its distribution function F(x)   [A.U CBT A/M 2011]

Solution :