Problems based on bilinear transformation

 PROBLEMS BASED ON BILINEAR TRANSFORMATION

Example 3.5.11 Find the bilinear transformation that maps the points z = 0, -1, i into the points w = i, 0, ∞ respectively.  [A.U. A/M 2015 R-13, A.U N/D 2013, N/D 2014]

Solution :

Given: z₁ = 0, z₂=-1, z₃ = i

w₁ = i, w₂ = 0, w₃ = ∞

Let the required transformation be

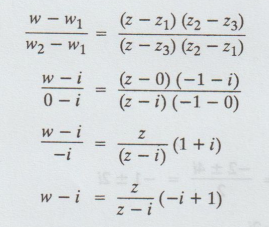
w – i = z/z – i (-i + 1)

w = z/z – i (-i + 1) + i = -iz + z + iz + 1 / (z – i) = z + 1/z - i

Aliter: Given: z₁ = 0, z₂ = -1, z₃ = i

w₁ = i, w₂ = 0, w₃ = ∞

Let the required transformation be

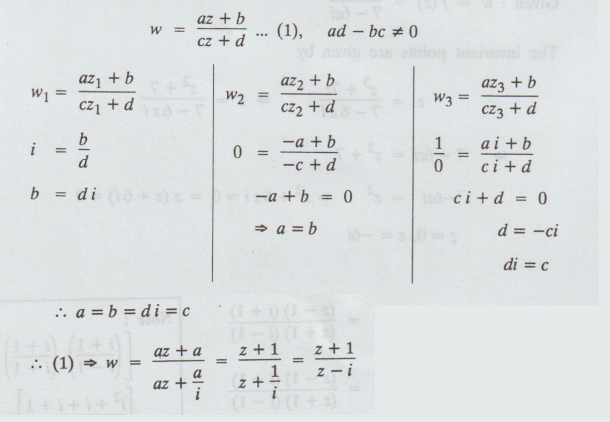
w = az + a/az + a/i = z + 1/z + 1/i = z + i /z - i

 

Example 3.5.12. Find the bilinear transformation that maps the points ∞, i, 0 onto 0, i, ∞ respectively. [Anna, May 1997] [A.U N/D 2012][A.U A/M 2017 R-08]

Solution: Given: z₁ = ∞, z₂ = i, z₃=0 & w₁ = 0, w₂ = i, w₃ = ∞

Let the required transformation be

 

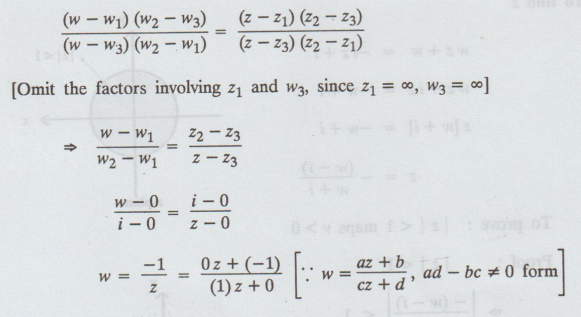
Example 3.5.13. Find the bilinear transformation which maps the points 1, i, -1 onto the points 0, 1, ∞, show that the transformation maps the interior of the unit circle of the z-plane onto the upper half of the w plane. [A.U. May 2001] [A.U M/J 2014] [A.U D15/J16 R-13]

Solution: Given: z₁ = 1, z₂ = i, z₃ = -1

w₁ = 0, w₂ =1, w₃ = ∞

Let the transformation be

 

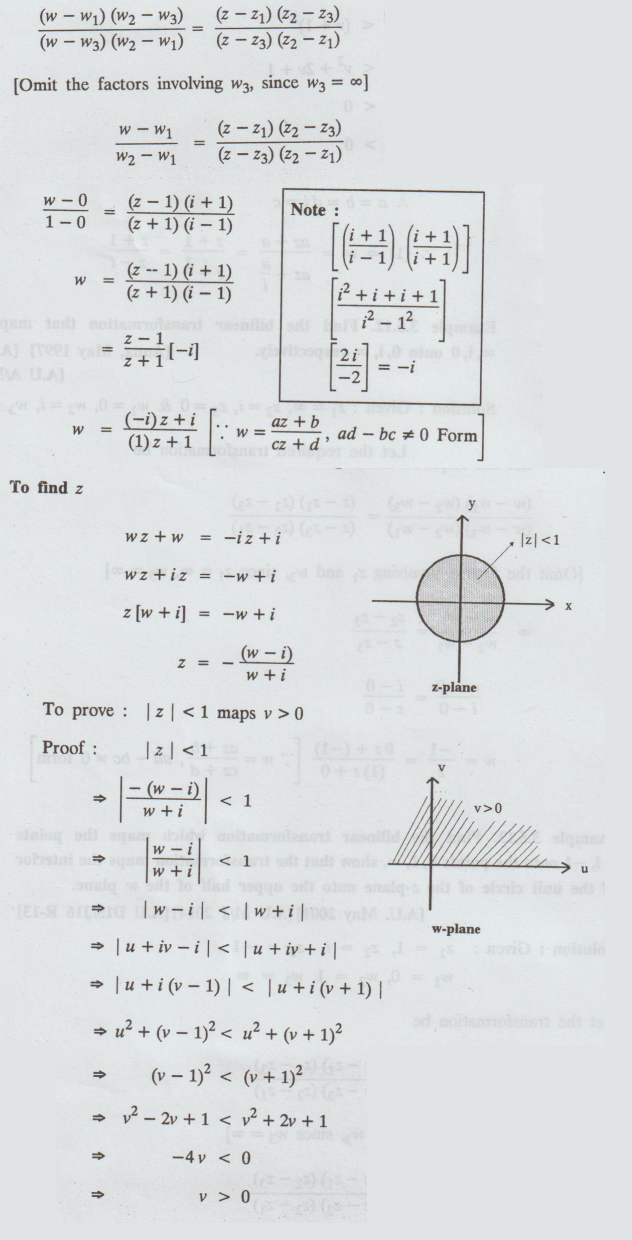
Example 3.5.14. Find the bilinear transformation which maps the points z = -2i, i, ∞ onto the points w = 0, -3,1/3 respectively. Find the image of | z❘ < 1.

Solution: Given: z₁ = -2i, z₂ = i, z₃ = ∞

w₁ = 0, w₂= -3 , w₃ = 1/3

Let the required transformation be

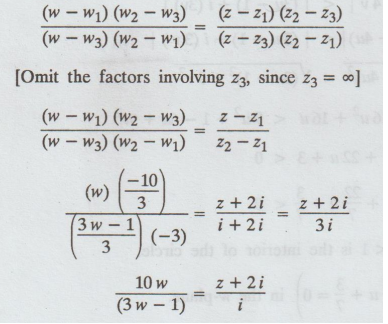
10 w/(3w-1) = z + 2i/ i

10 wi = 3 wz + 6wi – z - 2i

10wi - 6wi = 3wz-z-2i

4wi-3wz = -z - 2i

w[4i - 3z] = -[z + 2i]

w = - [z + 2i]/[4i-3z] = z + 2i/3z – 4i

w = (1) z + 2 i/3z + (-4 i) [ w = az + b/cz + d, ad – bc ≠ 0 Form]

To find z

3wz - 4wi = z + 2i

3wz - z = 4wi + 2i

z (3w - 1) = 2i (1 + 2w)

z = 2i (1+2w)/3w – 1

To find the image of | z | < 1

| z | < 1⇒

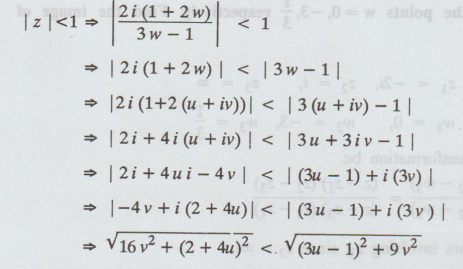
16 v² + 4 + 16 u² + 16u < 9 u² + 1 − 6u + 9v²

⇒ 7 u² + 7 v² + 22 u + 3 < 0

⇒ u² + v² + 22/7 u + 3/7 < 0

The image of | z |< 1 is the interior of the circle.

 (u² + v² + 22/7 u + 3/7 = 0) in the w-plane.

 

Example 3.5.15. Show that the condition for the transformation w = az + b/cz + d to transform the unit circle in the w plane is a straight line in the z plane if |a| = |c|.

Solution: The transformation w = az + b / cz + d w = a(z + b/a) / c(z + d/c)

Given: |w| = 1 (unit circle in w-plane)

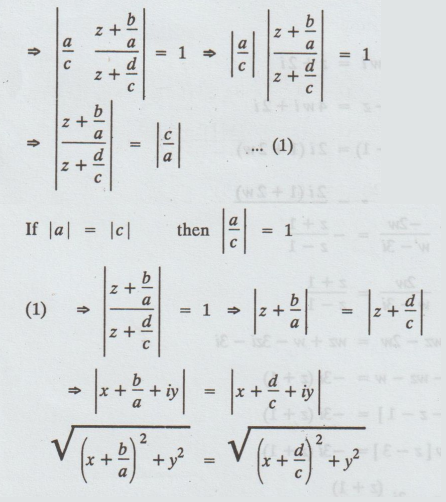
squaring we get

(x + b/a)² + y² = (x + d/c)² + y²

(x + b/a)²  = (x + d/c)²

2x b/a + b²/a² = 2x d/c – d²/c² = 0

x [ 2b/a – 2d/c ] + [ b²/a² – d²/c² ] = 0

which represents a straight line in z-plane

 

Example 3.5.16. Determine the billinear transformation that maps the points -1,0,1, in the z plane onto the points 0,i,3i in the w plane. [ Anna, May 1999 ]

Solution :

Given : z₁ = -1, z₂ = 0, z₃ = 1

w₁ = 0 , w₂ = i, w₃ = 3i

Let the required transformation be

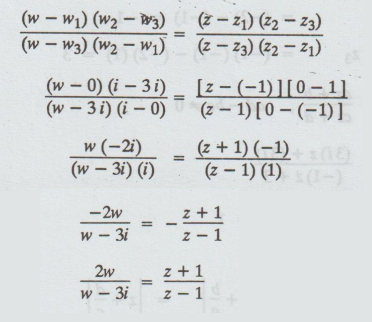
2wz - 2w = wz + w - 3zi - 3i

2wz - 2w - wz - w = -3i (z + 1)

w[2z – 2 – z -1] = -3i (z + 1)

w[z - 3]= -3i (z + 1)

w = -3i (z + 1)/(z - 3) [ w = az + b/cz + d,ad - bc #0 Form]

Note: Either image or object or both are infinity should not apply the following Aliter method.

Aliter :

Given: z₁ = -1, z₂ = 0, z₃ = 1

w₁ = 0 , w₂ = i, w₃ = 3i

Let the required transformation be

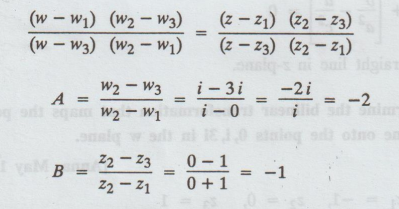
a = Aw₁ – Bw₃ = 0 + 3i = 3i

b = Bw₃z₁ - A w₁z₃ = (-1) (3i) (-1) - 0 = 3i

c = A – B = (-2) – (-1) = -1

d = Bz₁ - Az₃ = (-1)(-1) – (-2)(1) = 3

We know that, w = az + b/cz + d, ad - bc #0

w =  (3i)z + (3i)/ (-1)z + 3

 

Example 3.5.17. Find the bilinear transformation which maps z = 1, i, -1 respectively onto w = 1, 0, -i. [A.U, May 2001] [A.U Tvli N/D 2009] [A.U N/D 2014 R13, A/M 2015 R8] [A.U April 2016 R-15 U.D][A.U A/M 2019 R-17]

Solution :

Given: z₁ = 1, z₂ = i, z₃ = -1

w₁ = i , w₂ = 0, w₃ = -i

Let the required transformation be

a = Aw₁ – Bw₃ = (-1)(i) – (-i)(-i) = -i + 1

b = Bw₃z₁ - A w₁z₃ = (-i)(-i)(1) – (-1)(i)(-1) = - 1- i

c = A – B = (-1) – (-i) = -1 + i

d = Bz₁ - Az₃ = (-1)(1) – (- 1)(- 1) = -i - 1

We know that, w = az + b/cz + d, ad - bc ≠ 0

 

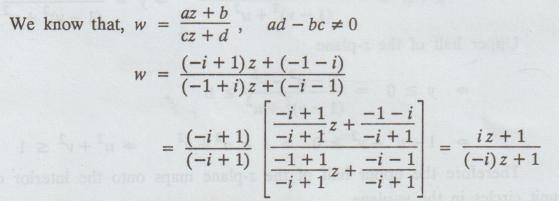
Example 3.5.18. Find the bilinear transformation which maps z = 0 onto w = -i and has -1 and 1 as the invariant points. Also show that under this transformation the upper half of the z plane maps onto the interior of the unit circle dos te w plane. [A.U A/M 2017 R-13]

Solution: Given: z₁ = 0, z₂ = -1, z₃ = 1

w₁ = -i , w₂ = -1, w₃ = 1

Let the required transformation be

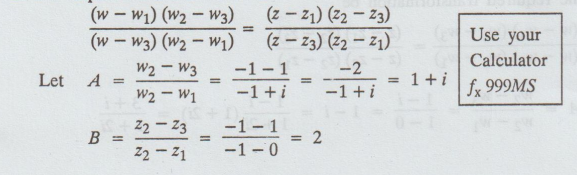
a = Aw₁ – Bw₃ = (1 + i)(-i) – (2)(1) = -i + 1 – 2 = - i - 1

b = Bw₃z₁ - A w₁z₃ = (2)(1)(0) – (1 + i ) (- i)(1) = -  i - 1

c = A – B = (1+ i ) – 2 =  i - 1

d = Bz₁ - Az₃ = (2)(0) – (1 + i )(1) = - (i + 1)

We know that, w = az + b/cz + d, ad - bc ≠ 0

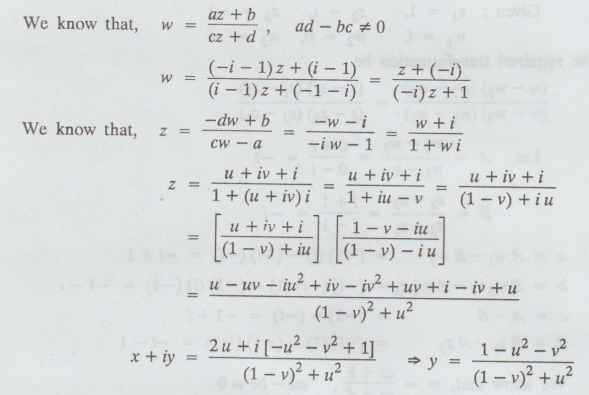
Upper half of the z-plane

⇒ y ≥ 0 ⇒ 1 -u² - v² /(1 - v)² + u² ≥ 0

⇒ 1- u² - v² ≥ 0 ⇒ 1 ≥ u² + v²  ⇒  u² + v² ≤ 1

Therefore the upper half of the z-plane maps onto the interior of the unit circles in the w-plane.

 

Example 3.5.19. Find the Bilinear transformation that maps the points 1+i, -i, 2 - i of the z-plane into the points 0, 1, i of aid the w-plane. [A.U. M/J 2007, N/D 2007]

Solution: Given: z₁ = 1 + i , z₂ = -i, z₃ = 2 - i

w₁ = 0 , w₂ = 1, w₃ = i

Let the required transformation be

 = 2 – i – 4i – 2/ -  4 – 1 = -5i/-5 = i

Example 3.5.20  the bilinear transformation which maps the points points w = -1, -i, 1. Show that under this transformation the z-plane maps on to the interior of the unit circle | w | = 1  [A.U A/M 2018, R-17]

Solution: Given: z₁ = -1 , z₂ = 0, z₃ = 1

w₁ = -1 , w₂ = -i, w₃ = 1

Let the required transformation be

The upper half of the z-plane maps on the interior of the circle | w | =  1