Electrical Machines: Unit III: b.Testing of D.C. Machines
Swinburne's Test or No Load Test
Advantages, Disadvantages, Solved Example Problems | Testing of D.C. Machines
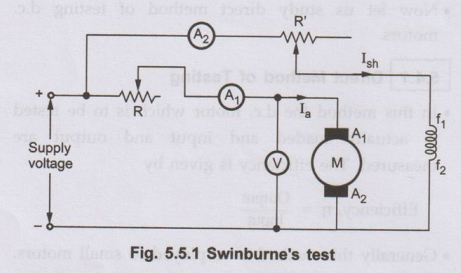
This is indirect method of testing d.c. motors in which flux remains practically constant i.e. specially in case of shunt and compound motors. Without actually loading the motor the losses and hence efficiency at different loads can be found out.
Swinburne's Test or No Load Test
AU May-04.05,06,08.16.17.
Dec.-04,06,08,16
•
This is indirect method of testing d.c. motors in which flux remains
practically constant i.e. specially in case of shunt and compound motors.
Without actually loading the motor the losses and hence efficiency at different
loads can be found out.
• The motor is run on no load at
its rated voltage. At the starting some resistance is connected in series with
the armature which is cut when motor attains sufficient speed. Now the speed of
the motor is adjusted to the rated speed with the help of shunt field rheostat
as shown in the Fig. 5.5.1.
•
The no load armature current Ia is measured by ammeter A1
whereas the shunt current is measured by ammeter A2. om air to bac
•
If V is the supply voltage then motor input at no load will be,
Power
input at no load = V (Ia+Ish) watts
There
will be Cu loss in the field winding which will be given as,
Field
copper loss = V × Ish
Let
Ra be the resistance of armature,
Armature
copper loss = Ia2 Ra
•
Thus the stray losses which includes iron, friction and windage losses can be
obtained as,
Stray
losses = Input at no load - Field copper losses - No load armature copper
losses
Stray losses =V (Ia+Ish)
- (V × Ish) - (Ia2 Ra) = Wa
•
In the field and armature windings there will be copper loss due to flow of
current which will increase the temperature of the field and armature winding
when the motor is loaded. This increase in temperature will affect their
resistances.
•
Thus the new value of field resistance R'sh and that of armature R'a
can be found by considering that rise in temperature as about 40 °C.
If
α1 = Resistance temperature coefficient of copper at room
temperature
R'a
= Ra (1+α1×40)
At
room temperature the shunt field winding resistance will be,

Now
if we want to find the efficiency of the motor at say ¼ th full load. It can be
calculated as follows,
Let
IF.L = Full load current of motor
WF
=Field copper loss
W
= Stray losses

This
is the efficiency of motor when the load on motor is ¼ th of full load which can be found without
loading the motor. The efficiencies at other loads can be calculated similarly.
1. Advantages
1.
Since constant losses are known, the efficiency can be estimated at any load.
2.
The method is convenient and economical as less power is required for testing
even a large motor i.e. only no load power is to be supplied. gorb
3.
The motor is not required to be loaded i.e. only test to be carried out is the
no load test.
2. Disadvantages
1.
In this method, the iron losses are assumed to be constant which is not the
true case as they change from no load to full load. Due to armature reaction at
full load there will be distortion in flux which will increase the iron loss.
2.
The only test which is carried out is the no load test. Hence it is difficult
to know whether there will be satisfactory commutation at full load.
3.
We have assumed that there is rise in temperature of 40 °C at full load which
cannot be checked actually as we are not actually loading the motor.
4.
As it is a no load test it cannot be performed on a series motor.
Efficiency as a motor :
Input
= V I, Armature copper loss = 1a2 Ra
W
= Stray losses, WF = Field copper loss
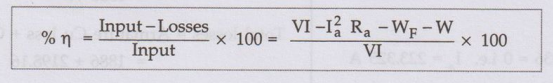
Efficiency as a generator:
Output
= VtIL, Armature copper loss = Ia2Ra
W
= Stray losses, WF = Field copper loss
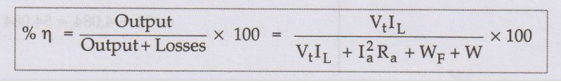
Ex. 5.5.1
The no load test of a 44.76 kW, 220 V
d.c. shunt motor gave the following results: Input current = 13.25 A, Field
current = 2.55 A, Resistance armature at 75 °C = 0.032 Ω, Brush drop = 2 V
Estimate the full load current and efficiency.AU May-16, Marks 16
Sol. :
Sol
: No
load current I = 13.25 A,
Full
load power output = 44.76 kW = 44760 W
No
load power input = V.I. = 220 × 13.25 = 2915 W
In
case of shunt motors, I = Ish + Ia
Ia
= I - Ish = 13.25 - 2.55 = 10.7 A
No
load armature copper loss = Ia2 . Ra = (10.7)2
(0.032) = 3.664 W
Loss
due to brush drop = 2 × 10.7 = 21.4 W
Constant
losses = No load input - No load armature
Cu
loss - Loss due to brush drop
=
2915 - 3.664 - 21.4 = 2889.936 W
Now
let Ia be the full load current in armature.
..
Full load motor input current,
I
= Ia + Ish = (Ia
+ 2.55) A
Full
load motor input = V.I. = 220 (Ia + 2.55) W
I
= Ia + Ish = (Ia + 2.55) A
Full
load motor input = V.I.= 220 (Ia + 2.55) W
Motor
input = Motor output + Total Losses
=
Motor output + constant loss + brush loss + armature Cu loss
220
(Ia + 2.55) = 44760 + 2889.936 + 2 Ia + Ia2
Ra
=
44760 + 2889.936 + 2 Ia + Ia2 (0.032)
0.032
Ia2 + 2 Ia - 220 Ia + 44760+
2889.936
-
(220) (2.55) = 0
0.032
Ia2 - 218 Ia + 47088.936 = 0 i.e. Ia
= 223.325 A
Full
load motor input current = 223.325 + 2.55
=
225.875 A
Full
load motor input = V . I = (220) (225.875)
=
49692.5 W
Full
load motor efficiency = Output / Input × 100
=
44760 / 49692.5 × 100 = 90. 074%
Ex. 5.5.2 A
50 kW, 440 V, shunt generator having an
armature circuit resistance including the interpole winding of 0.15 at normal
working temperature was run as a shunt motor on no load at its rated voltage
and speed. The total current drawn by the motor was 5 A, including shunt field
current of 1.5 A. Calculate the efficiency of the shunt generator at i) Full
load ii) 3/4th load and iii) Half load.
Sol. :

Ex. 5.5.3 A 500 V, D.C. shunt motor takes a
total current of 5 A when running unloaded. The resistance of armature circuit
is 0.25 Ω and the field resistance is 125Ω. Calculate the efficiency and output
when the motor is loaded and draws a current of 100 A.AU Dec.-06, Marks 6
Sol. :

Ex. 5.5.4
A 220 V, D.C. shunt motor takes 4 A at no-load
when running at 700 r.p.m. The field resistance is 100 ohm. The resistance of
armature at standstill gives a drop of 6 volts across armature terminals when
10 A pass through it.
Calculate i) Speed on load ii)
Torque in N-m and iii) Efficiency: The normal input of the motor is 8 kW. AU: Dec.-08, Marks 16
Sol. :

Review Questions
1. With neat circuit
diagram explain how will you conduct Swinburne's test. Also show how to
calculate the efficiency when the machine is running a) as a motor b) as a
generator. Also state the merits and demerits of this method. AU: Dec.-04, 16,
May-04, 05, 08, 17, Marks 16
2. A 440 V d.c. shunt motor takes a no load current of 2.5 A. The resistance of the shunt field and the armature are 550 Ω and 1.2 Ω respectively. The full load line current is 32 A. Find the full load output and the efficiency of the motor.
(Ans.: 83.91 %)
3. A 80 h.p., 250 V
d.c. shunt motor runs on full load with a speed of 1200 r.p.m. The armature
resistance is 0.04 Ω and shunt field resistance is 250 Ω. Determine the
mechanical power developed on full load in kW. Assume full load efficiency of
the motor as 80 %.
If now the load on the motor is completely removed and it is made to run light, find its no load speed and no load current drawn from the supply. Assume stray losses constant on all load conditions.
(Ans.: 70.812 kW, 1250.9122 r.p.m.)
4. A 250 V, d.c. shunt motor takes a full load current of 67 A. Its armature resistance is 0.15 Ω and shunt field resistance is 166.67 Ω. When running on no load, the current drawn by the motor is 6.5 A and the speed as 1280 r.p.m. Determine i) Full load speed ii) Speed regulation iii) H.P. rating of the machine iv) Full load efficiency.
(Ans. 1233.396
r.p.m., 3.78%, 19.42 h.p., 86.47%)
5. A 400 V shunt motor takes 4.1 A when running light at 950 r.p.m. The armature resistance is 0.8 Ω, the total brush drop is 2 V and Rsh = 250 Ω. Determine full load efficiency, full load regulation and h.p. output when full load current is 50 A. Assume 5 % armature reaction.
(Ans.: 82.03%, 5.26
%, 22.3 h.p.)
6. A 10 kW, 250 V,
d.c. shunt motor with an armature resistance of 0.8 Ω and a field resistance of
275 Ω takes 3.91 A, when running light at rated voltage and rated
speed.
What conclusions can
you draw from the above data regarding machine losses?
Calculate the machine efficiency as a generator when delivering an output of 10 kW at rated voltage and speed and as a motor drawing an input of 10 kW. What assumption if any do you have to make in this computation.
(Ans. ng = 81.24%, = 78.07 %)
7. The full load
rating of 240 V, d.c. shunt motor running at 1000 r.p.m. is 8 kW. The armature
and shunt field resistance are 0.4 Ω and 240 Ω respectively. The efficiency at
full Determine,
i) No load current
ii) Speed when motor takes 12 A iii) The armature current when the torque
developed is 60 N-m.
(Ans. : IL
= 2.2814 A, N1 = 1045.95 r. p. m, Ia1 = 27.89 A)
8. A 230 V d.c. shunt motor is taking 5 A when running light. The armature resistance is 0.2 Ω and field circuit resistance is 115 Ω. For an input current of 72 A, calculate the shaft output and efficiency. Also calculate the armature current at wo which the efficiency is maximum.
(Ans. : η= 87.14%, Ia = 75.76 A)
Electrical Machines: Unit III: b.Testing of D.C. Machines : Tag: : Advantages, Disadvantages, Solved Example Problems | Testing of D.C. Machines - Swinburne's Test or No Load Test
Related Topics
Related Subjects
Electrical Machines I
EE3303 EM 1 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
