Probability and complex function: Unit I: Probability and random variables
2 Marks Questions and Answers
Probability and random variables | Probability and complex function
Probability and complex function: Unit I: Probability and random variables : '2 Marks' Questions and Answers
UNIT I
RANDOM VARIABLEST
'2 Marks' Questions and Answers
Type
1. Probability Axioms of probability - Conditional probability Baye's theorem -
Discrete and continuous random variable Moments m.g.f
1.
Define random variable. [A.U CBT N/D
2011]
A
random variable is a function that assigns a real number to each outcome in the
sample space for random experiment.
2.
Define discrete random variable with an example.
[A.U
CBT A/M 2011] [A.U A/M 2019 (R13) (RP)]
A
random variable whose set of possible values is either finite or countably
infinite is called discrete.
Example
number of transmitted bits received in error.
3.
Define continuous random variable with an example.
[A.U
A/M 2019 (R13) (RP)]
A
random variable X is said to be continuous if it takes all possible values
between certain limits say from real number 'a' to real number 'b'.
Example:
length, pressure, temperature, time, voltage, weight.
4.
Define : Probability mass function :
For
a discrete random variable X with possible values x1, x2,
xn a probability mass function is a function such that
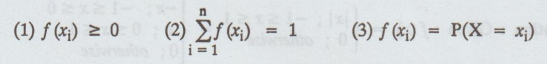
5.
Define cumulative distribution function of a discrete random variable X.
Solution:
The
cumulative distribution function of a discrete random variable X, denoted as F
(x), is
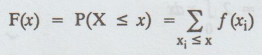
For
a discrete random variable X, F (x) satisfies the following properties.
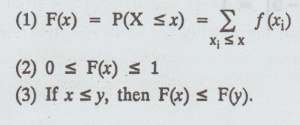
6.
Define mean (or) expected value of a discrete random variable.
Solution:
The
mean or expected value of the discrete random variable X, denoted as μ or E(X)
is
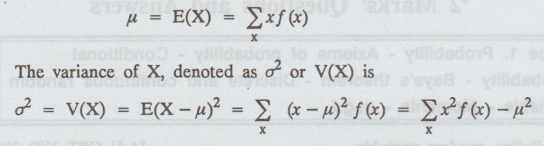
7.
Probability density function f (x) can be used to describe the probability dose
of a ................... random variable X.
Solution
: Continuous.
8.
Define probability density function. [p.d.f]
Solution:
See Text Book Page No. 1.80
9.
Define cumulative distribution function of a continuous random variable X.
Solution
: See Text Book Page No. 1.81
10.
Define mean or expected value of a continuous random variable X.
Solution
: See Text Book Page No. 1.81
11.
Test whether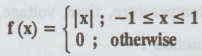 can be the probability density function of a
continuous random variable. [A.U N/D
2014] [A.U A/M 2015 R13]
can be the probability density function of a
continuous random variable. [A.U N/D
2014] [A.U A/M 2015 R13]
Solution:

12.
Define expectation of a random variable.
Solution:
Consider
a random variable X with p.m.f. p (x) (or) p.d.f. f(x). If g (X) is function of
X, then g (X) is a random variable. If E [g (x)] exists then
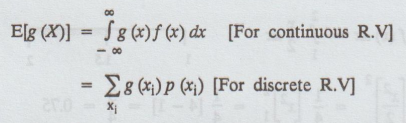
13.
Define nth moment about origin for a random variable.
Solution
: The nth moment about origin of a random
variable X is defined as the expected value of the nth power of X.
For
discrete random variable X,
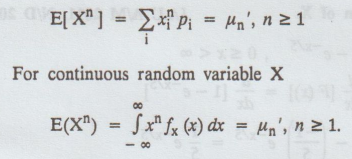
14.
Define moment generating function.
Solution
:
Def
:
Moment generating function of a random variable X about the origin is defined
as as
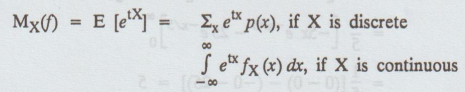
where
t being a real parameter assuming that the integration or summation is
absolutely convergent for some positive number h such that | t | < h.
15.
If the p.d.f of a random variable X is f (x) = x/2 in 0 ≤ x ≤ 2, find P (X >
1.5 / X > 1). [A.U A/M 2010]
Solution
:
Given:
f (x) = x/2, 0 ≤ x ≤ 2
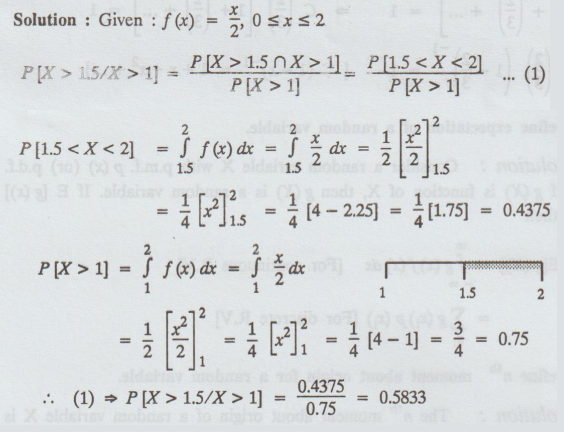
16.
The c.d.f of a continuous random variable is given by
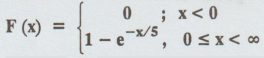
Find
the p.d.f and mean of X.
Solution:
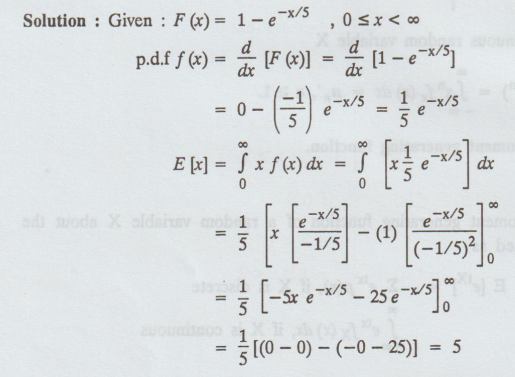
17.
Find C, if P [X = n] = C (2/3)n ; n = 1, 2, ...
Solution:
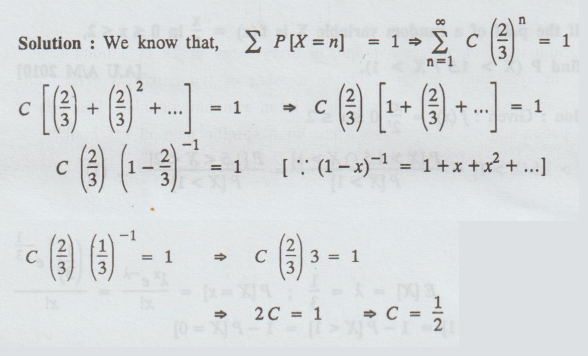
18.
An experiment succeeds twice as often as it fails. Find the chance that in the
next 4 trials, there shall be atleast one success. [A.U N/D 2012]
Solution:
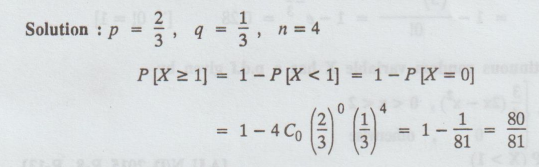
19.
A random variable X has cdf
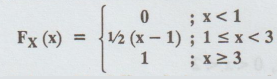
Find
the p.d.f of X and the expected value of X.
[AU M/J 2013, M/J 2014]
Solution:
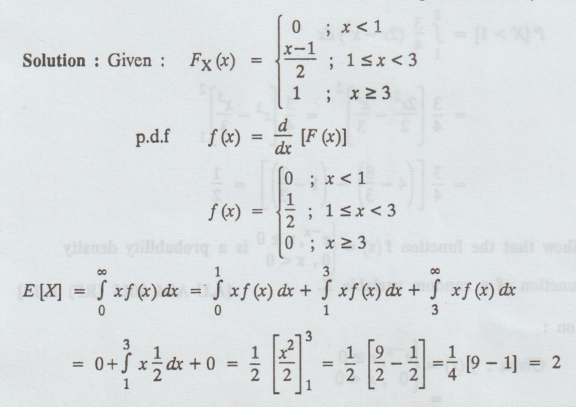
20.
Suppose that, on an average, in every three pages of a book there is one
typograhpical error. If the number of typographical errors on a single page of
the book is a Poisson random variable. What is the probability of at least one
error on a specific page of the book? [A.U
A/M 2015 R-8] [A.U A/M 2018 R-
Solution
:

21.
A continuous random variable X has a p.d.f given by
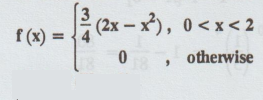 Find P (X > 1) [A.U N/D 2015 R-8,
R-13]
Find P (X > 1) [A.U N/D 2015 R-8,
R-13]
Solution
:
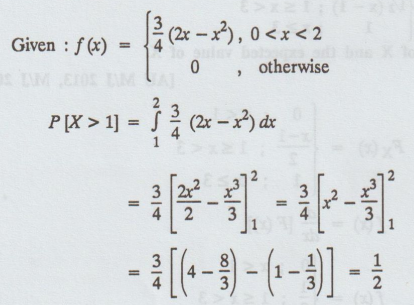
22.
Show that the function 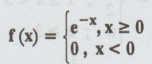 is a probability density function of a
random variable X. [A.U A/M 2015 (RP)
R-13]
is a probability density function of a
random variable X. [A.U A/M 2015 (RP)
R-13]
Solution
:
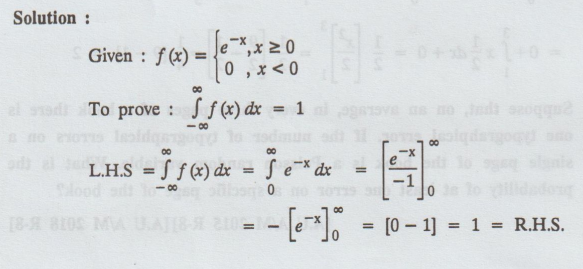
23. 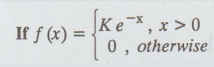 is the p.d.f of a random variable X, then the value of K. [A.U
M/J 2016 R-13 RP]
is the p.d.f of a random variable X, then the value of K. [A.U
M/J 2016 R-13 RP]
Solution:

24.
Find the expected value of the discrete random variable X with the probability
mass function 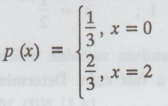 [A.U N/D 201613 R8]
[A.U N/D 201613 R8]
Solution
:
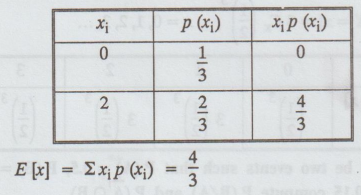
25.
A random variable X is known to have a distribution function F(x) = u(x) [1 - e-x2/b],
where b > 0 is a constant. Determine its density function.[A.U N/D 2016 R13
RP]
Solution
:
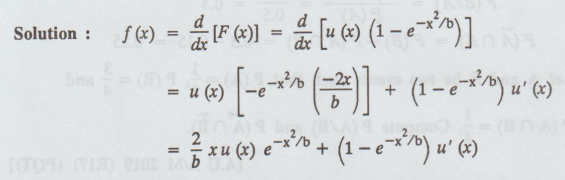
26.
Find the value of k for a continuous random variable x whose density function
is given by f (x) = kx2e-x, x ≥ 0
[A.U
N/D 2018 R-17] [PS]
Solution:
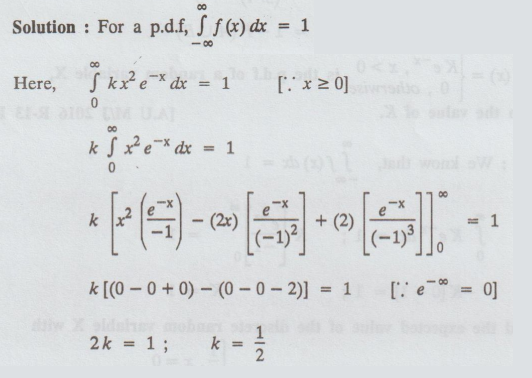
27.
Let X be the random variable which denotes the number of heads in three tosses
of a fair coin. Determine the probability mass function of X. [A.U N/D 2015
R-8] [A.U A/M 2019 R13 (PQT)]
Solution
:
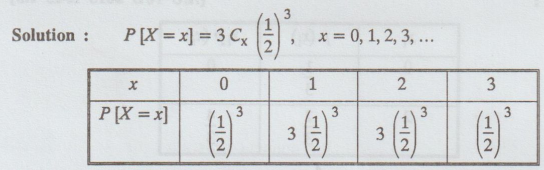
28.
Let A and B be two events such that P (A) = 0.5, P (B) = 0.3 and P(A∩B) = 0.15
compute P (B/A) and 
Solution:
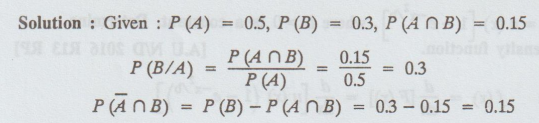
29.
Let A and B be two events such that P(A) = 1/3, P(B) = 3/4 and P(A∩B) = 1/4, Compute P (A/B) and  [A.U A/M 2019 (R17) (PQT)]
[A.U A/M 2019 (R17) (PQT)]
Solution
:
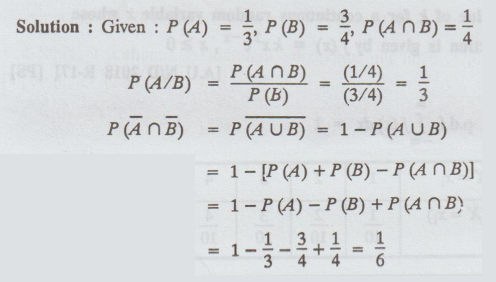
30.
A bag contains 8 white and 4 black balls. If 5 balls are drawn at random, what
is the probability that 3 are white and 2 are black? [A.U N/D 2019 (R17)-PQT]
Solution
:
Total
number of balls = 8+ 4 = 12
S
= {5 balls are taken out of 12}
n
(S) = 12 C5 = 12.11.10.9.8 / 1.2.3.4.5 = 792
The
number of favourable out comes
(i.e.,
3 are white and 2 are black)
=
n (A) = 8C3 × 4 C2
=
336
P(A)
= n (A) / n (S) = 336 / 792 = 14 / 33 = 0.4242
31.
Let Mx (t) = 1 / 1 − t | t | < 1, the moment generating function of R.V.X. Find
E [X] and E [X2]
[A.U
N/D 2019 (R17) PQT]
Solution
:
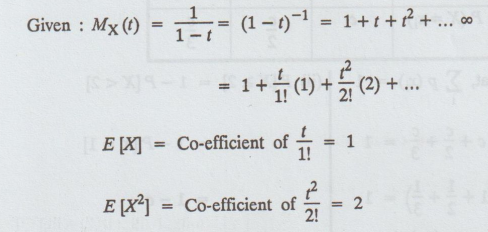
32.
A random variable X has probability mass function P (X = x) = x/10, x = 1, 2,
3, 4. Find the cumulative distribution function, F(x) of X. [A.U. A/M 2019
(R17) PQT]
Solution
:

33.
The R.V.X has p.m.f P (X = x) = 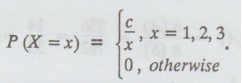
Obtain:
(i) The value of 'c', (ii) P (X ≥ 2)
[A.U N/D 2019 (R17) R.P]
Solution
:
34.
Show that for any events A and B in S,

Solution:
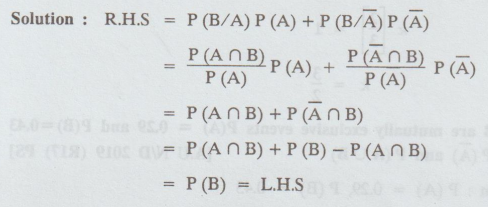
35.
The moment generating function of a random variable X is given by M (t) = e3
(et -1). What is P (X = 0] ?
Solution:
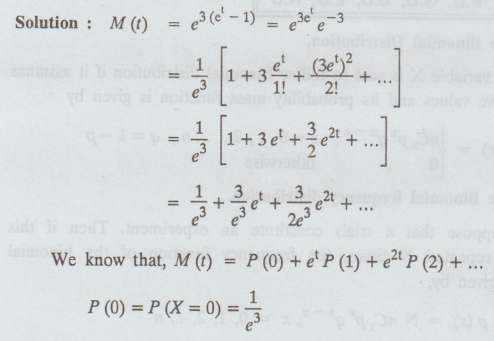
36.
The probability density function of the random variable X is given by
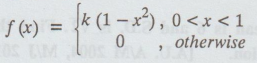
Solution:
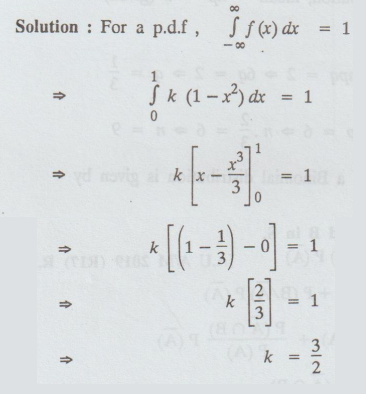
37.
If A and B are mutually exclusive events P(A) = 0.29 and P(B) = 0.43 then find 
Solution:
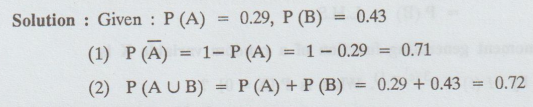
Probability and complex function: Unit I: Probability and random variables : Tag: : Probability and random variables | Probability and complex function - 2 Marks Questions and Answers
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
