Probability and complex function: Unit II: Two dimensional random variables
2 Marks Questions and Answers
Two dimensional random variables | Probability and complex function
Probability and complex function: Unit II: Two dimensional random variables : '2 Marks' Questions and Answers
UNIT II
TWO DIMENSIONAL RANDOM VARIABLES
'2 Marks' Questions and Answers
1.
Show that Cov2 (X, Y) ≤ Var (X). Var (Y) [A.U. N/D 2004]
Solution:
Let X and & Y be 2 R.V's. For any real number ɑ,
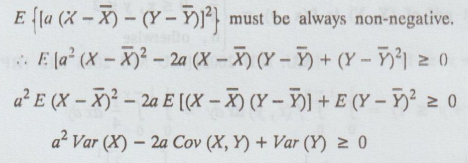
This
is a quadratic in 'a' and is always non-negative so the discreminent must be
non-positive.
[Cov (X, Y)]2 ≤ Var(X). Var (Y)
2.
Find the acute angle between the two lines of regression.
[A.U
A/M 2019 (R8) RP] [A.U. AM 1003) [A.U. A/M 2011]
Sol.
Angle
between the lines, is given by
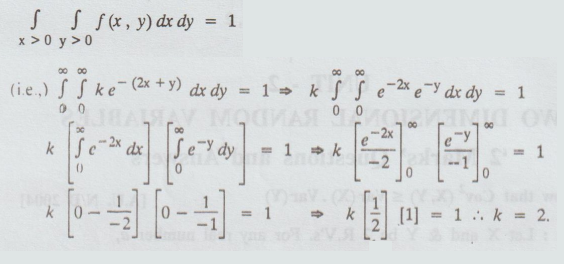
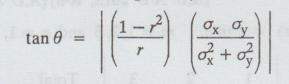
3.
If X and Y are independent random variables with variance 2 and 3, then find
the variance of 3X + 4Y.
[A.U. A/M 2003, M/J 2013] [A.U A/M 2018 R-08]
Sol.
R.V's X and Y are independent R.V's with variance 2 and 3.
(i.e.,)
Var (Y) = 2 and Var (Y) = 3
Consider
Var (3X + 4Y)
Var
(ax) = a2 Var (X).
=
32 Var (X) + 42 Var(Y) = 9 × 2 + 16 × 3 = 18 + 48 = 66
4.
If two random variables X and Y have probability density function (p.d.f) f(x,
y) = ke-(2x+y) for x, y > 0. Find 'k'.
Solution
:
By
the property of the joint pdf,
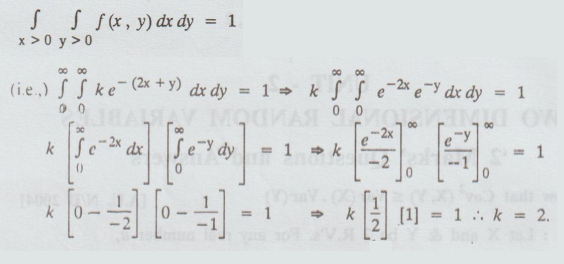
5.
If the joint pdf of (X, Y) is f(x, y) = 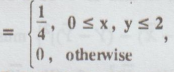 find P (x + y ≤
1) [A.U. N/D 2005] [A.U M/J 2016 R13
(RP))
find P (x + y ≤
1) [A.U. N/D 2005] [A.U M/J 2016 R13
(RP))
Solution
:
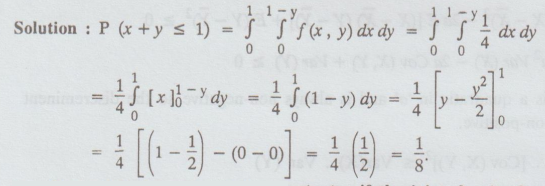
6.
Determine the value of the constant c if the joint density function of two
discrete random variables X and Y is given by p (m, n) = c mn, m = 1, 2, 3 and
n = 1,2,3 [A.U N/D 2015, R-8] [A.U A/M
2017 R-8]
Solution:
Given:
p (m, n) = c m n, m = 1, 2, 3 and n = 1, 2, 3

7.
What do you mean by correlation between two random variables? [A.U A/M 2015 K8]
Solution
Degree
of relationship and nature of relationship.
8.
The joint probability mass function of a two dimensional random variable (X, Y)
is given by p (x, y) = k (2x + y), x = 1, 2 and y = 1, 2, where k is a
constant. Find the value of k. [A.U N/D 2015 R-13]
Solution:
Given:
P (x,y) = k (2x + y)
x
= 1, 2 and y = 1,2
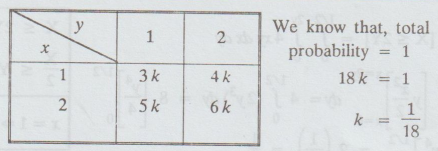
9.
Let (X, Y) be a two-dimensional random variable. Define co-variance of (X, Y).
If X and Y are independent. What will be the covariance of [ (X, Y)? [A.U M/J
2016, R-13 RP]
Solution:
Cov.
(X, Y) = E [(X-E (X)) (Y - E (Y))]
=
E [XY]-E[X] E [Y]
If
X and Y are independent, then E [XY] = E[X]E[Y]
Cov.
(X, Y) = E[X]E[Y] - E [X]E[Y] = 0
10.
Can y = 5 + 2.8x and x = 30.5y be the estimated regression equation of y on x
respectively explain your answer.
Solution
:
byx
= 2.8, bxy = -0.5
r
= ± √(bxy) (byx) = imaginary
They
can not be estimated regression equations.
11.
The joint probability density function of the random variable x and is defined as
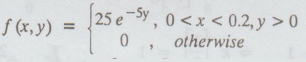
Find
the marginal PDF's of x and y.
Sol.
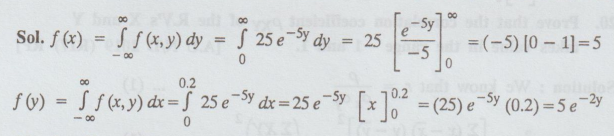
12.
Let X and Y be two independent R.Vs with Var(X) = 9 and Var(Y) = 3.
Find
Var(4X - 2Y + 6).
[A.U
M/J 2016 R13 (PQT)] [A.U N/D 2019 (R17) PQT)
Solution:
Given: Var (X) = 9, Var (Y) = 3
Var
[4X - 2Y + 6] = 42 Var (X) + (-2) 2 Var (Y)
=
(16) (9) + (4) (3)
=
144 + 12 = 156
13.
The joint probability density function of (X, Y) is
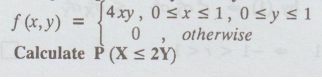
Calculate
P (X ≤ 2Y)
[A.U A/M 2019 (R17) PQT]
Solution
:
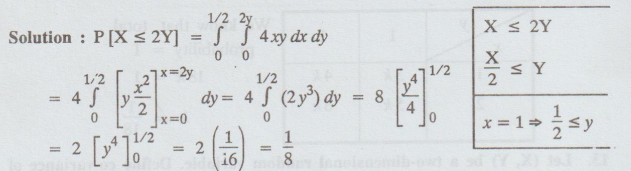
14.
Define covariance and coefficient of correlation between two random variables x
and y.
[A.U
A/M 2019 (R17) RP]
Solution:
Cov.
(X, Y) = EXY - EX]E[Y]
r
(X, Y) = Cov (X, Y) / σX = σY
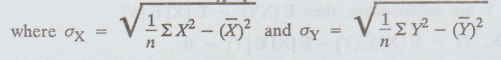
15.
The joint pdf of a bivariate random variable (X, Y) is given by
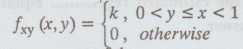 where k is a constant. Determine the value of k.
where k is a constant. Determine the value of k.
[A.U A/M 2019 (R17) RP]
Solution:
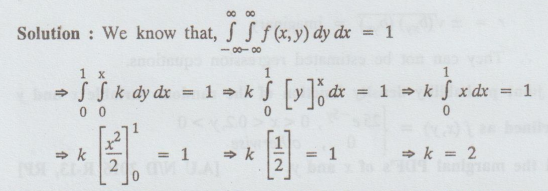
16.
Prove that the correlation coefficient PXY of the R.V's X and Y takes
value in the range -1 and 1.
Solution:
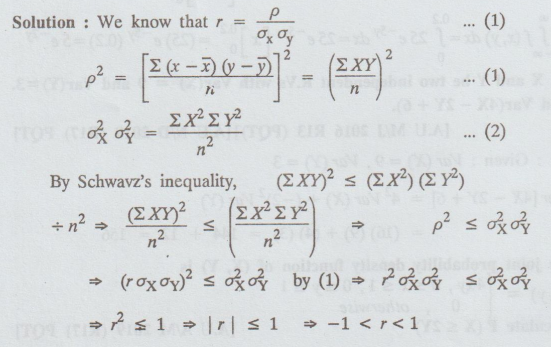
Probability and complex function: Unit II: Two dimensional random variables : Tag: : Two dimensional random variables | Probability and complex function - 2 Marks Questions and Answers
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
