22 factorial design

2² FACTORIAL DESIGN :

A major conceptual advancement in an experimental design is exemplified by factorial design. Factorial designs are frequently used in experiments involving several factors, where it is necessary to study the joint effect of the factors on a response.

In factorial designs, an assessment of each individual factor effect is based on the whole set of measurements so that a more efficient utilisation of experimental resources is achieved in these designs.

The most important of these special cases is that of k factors, each at only two levels. These levels may be quantitative, such as two values of temperature, time or pressure or they may be qualitative, such as two machines, two operators, the 'high' and 'low' level of a factor or perhaps the presence and absence of a factor.

A complete replicate of such a design requires 2 × 2 × … 2^k observations is called a 2^k factorial design.

Demerits :

Here, each factor is measured only at two levels, it is impossible to judge, whether the effects produced by variations in a factor are linear or perhaps, parabolic or exponential.

2² design :

2² is the simplest design of 2^k.

Two factors A and B each at two levels that it may be low and high levels of B the factor.

2² design can be represented geometrically as a square with the 2² = 4 runs, or treatment combinations, forming the corners of the square.

Here, we denote low and high levels of A and B, by the signs - and +. This is sometimes called the geometric notation for the design.

Example for 2² design :

The simplest factorial experiment contains two levels for each two factors. Suppose, an engineer wishes to study the total power used by each of two different motors, A and B, running at each of two different speeds, 2000 or 3000 RPM, the factorial experiment would consist of four experimental units: motor A at 2000 RPM, motor B at 2000 RPM, motor A at 3000 RPM, and motor B at 3000 RPM. Each combination of a single level selected from every factor is present once.

Two-level 2-Factor Full-Factorial experiment Design pattern :

Let the letters (1), a, b and ab also represent the totals of all n observations taken at these design points.

To find the main effect of A

We would average the observations on the right side of the square in the above figure. Where A is at the high level and subtract from this the average of the observations on the left side of the square, where A is at the low level or

The analysis of variance is completed by computing the total sum of squares SST (with 4n-1 d.f) as usual, and the error sum of squares SSE (with 4 (n - 1) d.f] by subtraction.

Analysis fo a 2² factorial experiments

(i) Let, y_ij = yield of the j^th treatment in the i^th block in a R.B.D = μ + a; + T_j + e_ij, i = 1, 2, 3, ... b, j = 1, 2, ... v, where ɑ_i  is the block effect, T; the treatment effect and e_ij the random error.

(ii) The experiment is carried out on a LSD,

y_ijk = μ + ß_i; + ɤj + Tk + e_ijk, i, j, k^th = treatment in the i^th row and j^th column.

For a 2² - experiment, we have 4 treatments and each block in a RBD is a complete replicate, for a LSD (it is a 4 × 4 LSD) each row, each column is complete replicate.

d.f. is as follows

The 3 d.f due to treatments are further partitioned as follows

due to

A : 1

AB : 1

Example 2.5.1

Factorial Designs [A.U N/D 2015 R-13]

Find out the main effects and interactions in the following 22-factorial experiment and write down the Analysis of Variance table :

Solution: Taking deviation from y = 37, weget

Example 2.5.2

From the 2² factorial design of table:  [A.U N/D 2011]

Example 2.5.3

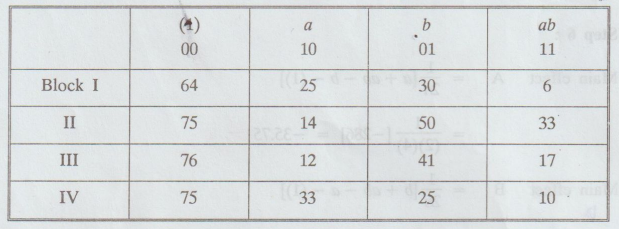
An experiment was planned to study the effect of sulphate of potash and super phosphate on the yield of potatoes. All the combinations of 2 levels of super phosphate [0 cent (b₀) and 5 cent (b) /acre] and two levels of sulphate of potash [0 cent (a₀) and 5 cent (a₁)/acre] were studied in a randomised block design with 4 replications for each. The (1/70) yields [lb. per plot = (1/70) acre obtained are given in Table : Analyse the data and give your conclusions.

[A.U A/M 2010] [A.U N/D 2021 (R-17)]

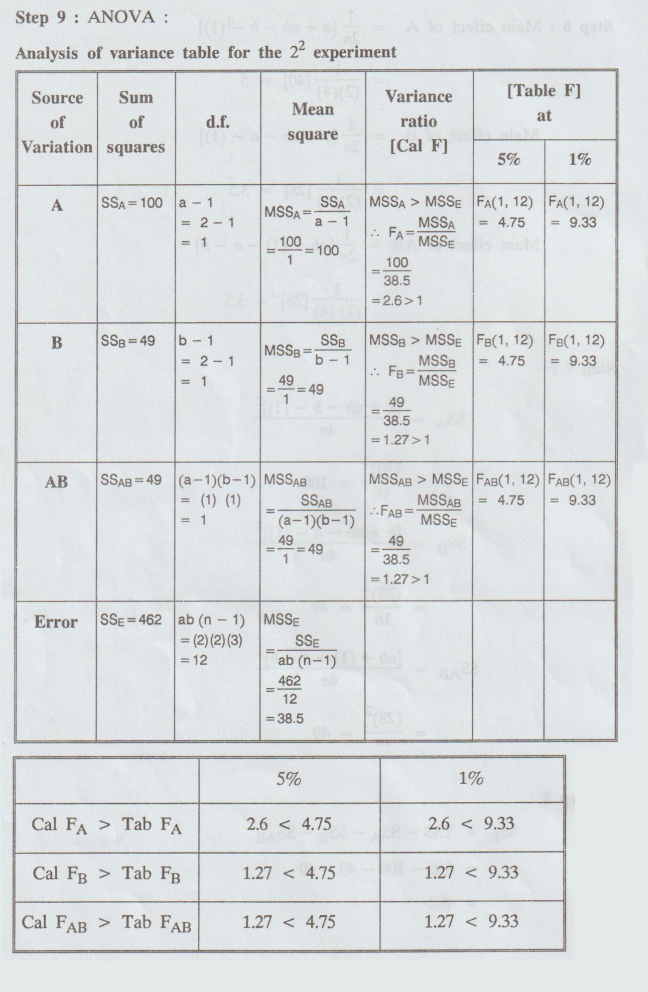
As in each of the cases, the computed value of F is less than the corresponding tabulated (critical) value, there are no significant main or interaction effects present in the experiment.