A.C. Analysis of Differential Amplifier using h-Parameters

A.C. Analysis of Differential Amplifier using h-Parameters

In the a.c. analysis, we will calculate the differential gain A_d, common mode gain A_c, input resistance R_i and the output resistance R0 of the differential amplifier circuit, using the h-parameters.

 

1. Differential Gain(A_d)

For the differential gain calculation, the two input signals must be different from each other. Let the two a.c. input signals be equal in magnitude but having 180° phase difference in between them. The magnitude of each a.c. input voltage V_S1 and V_S2 be V_S/2

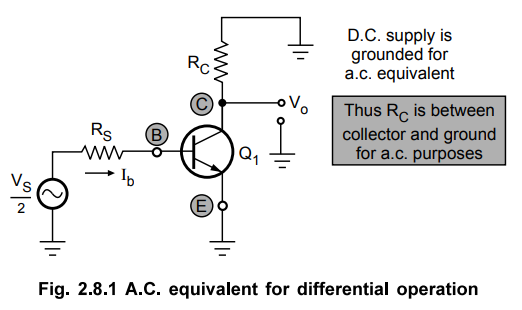
The two a.c. emitter currents I_e1 and I_e2 are equal in magnitude and 180° out of phase. Hence they cancel each other to get resultant a.c. current through the emitter as zero. This is already discussed in the section 2.8.1. Hence for the a.c. purposes emitter terminal can be grounded. The a.c. small signal differential amplifier circuit with grounded emitter terminal is shown in the Fig. 2.8.1. As the two transistors are matched, the a.c. equivalent circuit for the other transistor is identical to the one shown in the Fig. 2.8.1.

Thus the circuit can be analysed by considering only one transistor. This is called as half circuit concept of analysis.

The approximate hybrid model for the above circuit can be shown as in the Fig. 2.8.2, neglecting h_oe,

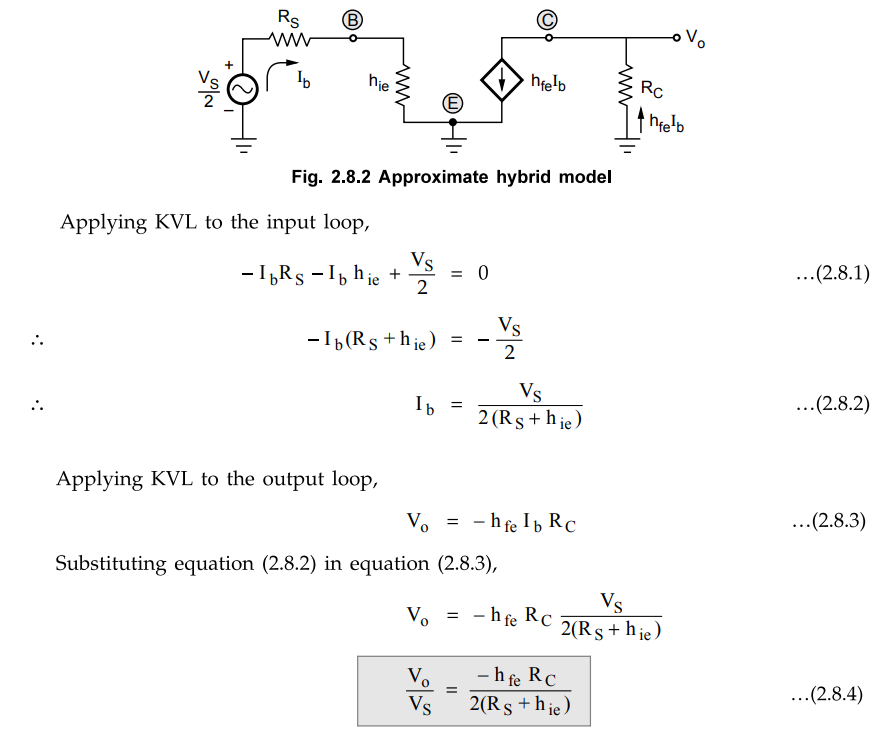
The negative sign indicates the phase difference between input and output.

Now two input signal magnitudes are V_S/2 but they are opposite in polarity, as 180^o out of phase.

 V_d = V₁ – V₂ = V_S / 2 – (-V_S/2) = V_S|

The magnitude of the differential gain A_d is

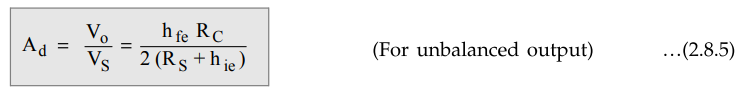
Where V_S = Differential input

Key Point The differential gain obtained in the equation (2.8.5) is for the circuit where output is measured with respect to ground. So it is unbalanced output.

We are interested to obtain Ad for the differential amplifier with the balanced output. Balanced output is across the two collectors of the transistors Q₁ and Q₂, which are perfectly matched. Such balanced output is double than that obtained above, with imbalanced output. Hence the expression for A_d with balanced output changes as

This is the differential gain for balanced output dual input differential amplifier circuit.

 

2. Common Mode Gain(A_c)

Let the magnitude of both the a.c. input signals be V_S and are in phase with each other. Hence the differential input V_d = 0 while the common mode input V_C is the average value of the two.

V_c = V₁ + V₂ / 2 = V_S + V_S / 2 …. (2.8.7)

While the output can be expressed as

V_o = A_c V_S  …. (2.8.8)

A_c = V_o / V_S  …. (2.8.8 (a))

But now both the emitter currents I_e1 = I_e2 = I_e, flows through R_E in the same direction.

Hence the total current flowing through R_E is 2 Ie.

As the two transistors are matched, a.c. equivalent of common mode operation can be shown, considering only one transistor, as in the Fig. 2.8.3. 

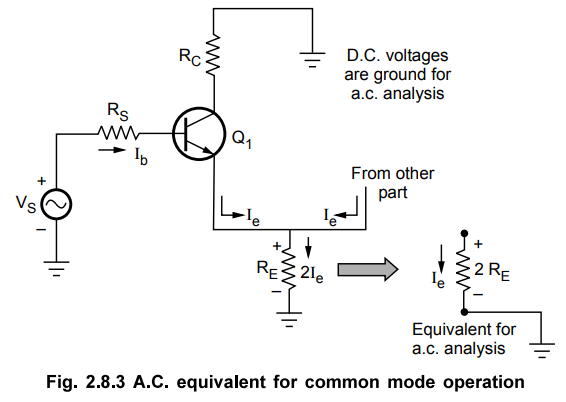
The approximate hybrid model for the above circuit can be shown as in the Fig. 2.8.4.

As the current through R_E is 2_Ie, for simplicity of derivation the current can be assumed to be Ie and effective emitter resistance as 2 R_E. Hence the emitter resistance is shown 2 R_E in the Fig. 2.8.4.

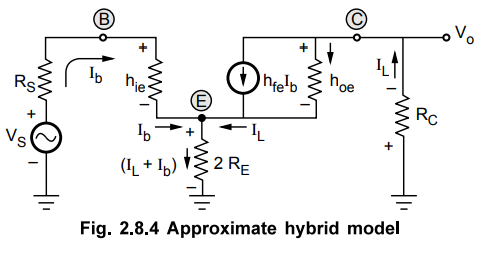
So Current through R_C = Load current I_L

Effective emitter resistance = 2 R_E

Current through emitter resistance = I_L + I_b

Current through h_oe = (I_L - h_fe I_b)

Applying KVL to the input side,

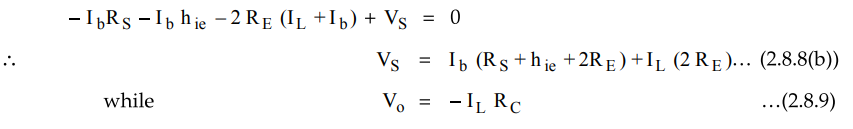
Negative sign due to the assumed direction of current. Applying KVL to the output loop,

Key Point   The expression for A_c remains same whether the output is balanced or unbalanced.

 

3. Common Mode Rejection Ratio (CMRR)

Once the differential and common mode gains are obtained, the expression for the CMRR can be obtained as,

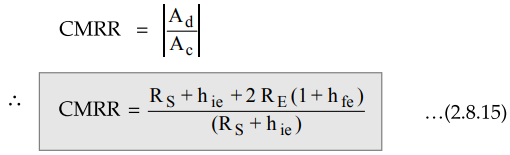
This is CMRR for dual input balanced output differential amplifier circuit.

 

4. Differential Input Impedance (R_i)

It is the equivalent resistance between one of the input and the ground when the other input terminal is grounded. Hence

R_i = V_S / I_b …. (2.8.16)

But referring to Fig. 2.8.2 and equation (2.8.1) we can write,

R_i =   2 (R_S + h_ie) …. (2.8.17)

For one transistor and input pair, the input resistance is RS +hie hence for dual input circuit the total input resistance is 2(R_S + h_ie), as the two circuits are perfectly matched.

Key Point This input resistance is not dependent on whether output is balanced or unbalanced.

 

5. Output Impendance (R_o)

It is defined as the equivalent resistance between one of the output terminals with respect to ground. As seen from the Fig. 2.8.2, the resistance between output terminal with respect to ground is RC.

R_o = R_C …. (2.8.18)

In the a.c. analysis of dual input, balanced output differential amplifier, it can be observed that the results are derived by considering only one transistor and one output at the time of analysis. And then due to matched pair of transistors, the results are derived for dual input, balanced output configuration. Hence the results for the remaining configurations can be directly obtained from the results derived earlier. And hence the summary of the differential amplifier circuit configurations is directly provided in the Table 2.8.1.

 

Example 2.8.1 The Fig. 2.8.5 shows dual input, balanced output differential amplifier configuration. Assuming silicon transistors with h_ie = 2.8 AΩ calculate

i) Operating point values

ii) Differential gain

iii) Common mode gain

iv) CMRR

v) Output if V_S1 = 70 mV peak to peak at 1 kHz and V_S2 = 40 mV peak to peak at 1 kHz.

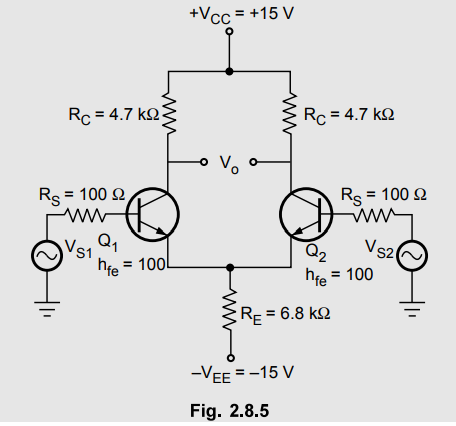
Solution : As the transistors are silicon,

 V_BE = 0.7 V

i) Operating point are I_CQ and V_CEQ

Key Point In practice A_cV_c can be neglected as com pared to AffVd «s common mode gain is always very small compared to differential gain.

 

6. Differential Amplifier with Constant Current Source

Without physically increasing the value of R_E, the RE is replaced by a transistor operated at a constant current.

Such a constant currrent source circuit gives the effect of a very high resistance without affecting the Q point values of the differential amplifier.

The differential amplifier using constant current bias circuit instead of R_E is shown in the Fig. 2.8.6.

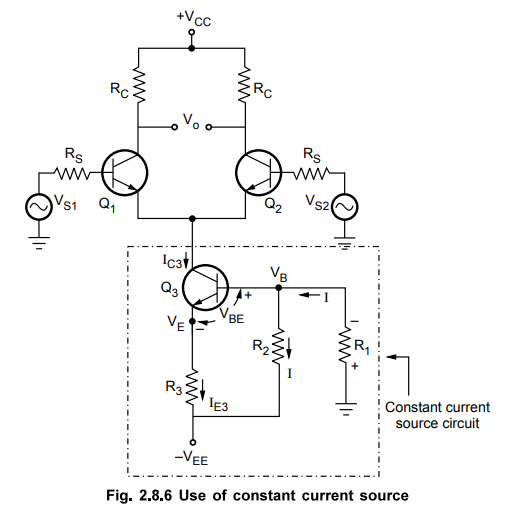
The transistor used is Q₃ and the values of R₁, R₂ and R₃ are selected so as to give the same operating point values for the two transistors Q₁ and Q₂.

a. Circuit Analysis

Let current through R₃ be I_E3 while current through R₁ is I.

Neglecting the base current of Q₃ which is very small due to large β_ac, we can assume that current through R₂ is also I.

Applying Kirchhoff's voltage law,

Thus as V_EE , R₁, R₂, R₃ and V_BE are constants, current I_C3 is almost equal to I_E3 and also constant. Thus circuit with transistor Q₃, acts as a constant current source.

Key Point The internal resistance of a constant current source is very high, ideally infinite. Hence this circuit makes the value of emitter resistance ideally infinite which reduces the common mode gain A_c ideally to zero. Thus as A_c tends to zero, CMRR tends to infinite.

Review Questions

1. Using the h-parameters, carry out the a.c. analysis of the differential amplifier. Find A_d, A_c , R_i and R_o for dual input balanced output.

2. The parameters for the differential amplifier are given as : R_C = 1 k Ω , R_S = 1 k Ω , h_fe= 1 k Ω and R_E = 2 M Ω Neglecting h_oe, calculate the difference mode gain and common mode gain. Hence calculate CMRR in dB. The amplifier is in dual input, balanced output configuration.

[ Ans.: 100.17 dB ]

3. For the differential amplifier shown in the Fig. 2.8.7, determine

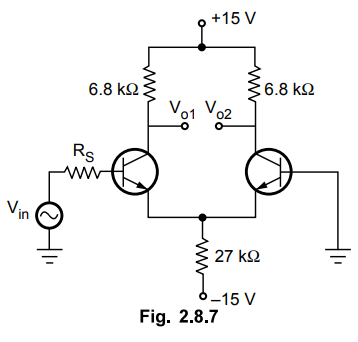
i) The voltages at the collector of each transistor

ii) The differential voltage gain.

Assume V_BE = 0.7 V, h_fe =100, h_ie = 3.9 k Ω and the source resistance as 1 k Ω

[ Ans.: 13.2 V, 34.69 ]

4. Draw the circuit of a symmetrical emitter coupled differential amplifier and derive the expression for the CMRR.

5. How common mode rejection ratio can be increased using constant current source ?