ADC (Analog to Digital Converter) using Op-amp

A/D Converters

May-03,04,05,06,07,08,09,10,11,12,14,16,18, Dec.-03,04,05,06,07,08,09,10,ll,16

The A/D conversion is a quantizing process whereby an analog signal is converted into equivalent binary word. Thus the A/D converter is exactly opposite function that of the D/A converter.

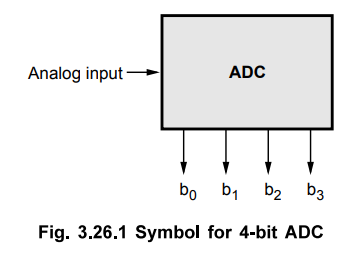
Fig. 3.26.1 shows symbol for A/D converter.

1. Performance Parameters of ADC

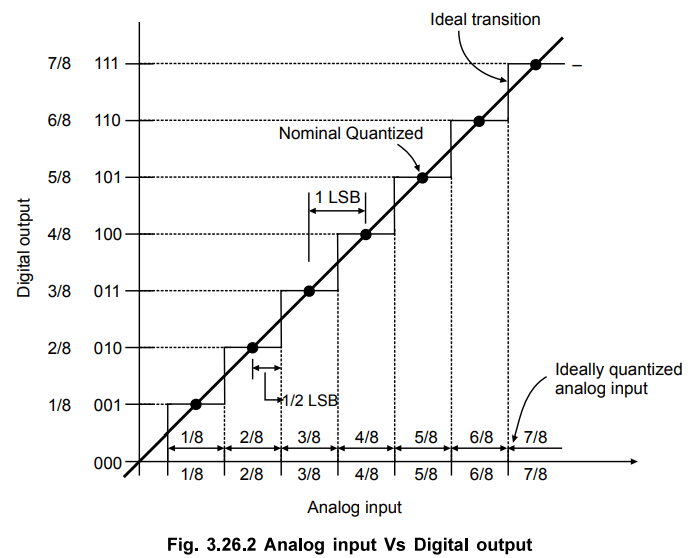
The Fig. 3.26.2 shows the digital output of an ideal 3 bit ADC plotted against the analog input voltage. 

a. Resolution

Fig. 3.26.2 shows eight (2³) discrete output states from 000₂ to 111₂, each step being  1/8 V apart. Therefore, we can say that expression of ADC resolution is the same as for 8 the DAC and is repeated here :

Resolution = 2ⁿ    ... (3.26.1)

Resolution is also defined as the ratio of a change in value of input voltage, V,-, needed to change the digital output by 1 LSB. If the full scale input voltage required to cause a digital output of all l's is V_iFS, then resolution can be given as

b. Quantization Error

Fig. 3.26.2 shows that the binary output is 011 for all values of V_i between 1/4 and 1/2 V_i. There is an unavoidable uncertainty about the exact value of V_i when the output is 011 This uncertainty is specified as quantization error. Its value is ± 1/2 LSB. 

It is given as, QE = V_iFS / (2ⁿ – 1)2   …. (3.26.3)

Increasing the number of bits results in a finer resolution and a smaller quantization error. The quantization error can be observed by continuously sampling a time-varying analog signal with an ADC, converting it back to analog with a DAC, and taking the difference between the two. The resulting sawtooth-like signal, called quantization noise.

The root mean square value of such signal, E_n can be given as

En = V_FS / 2ⁿ √12

This is related to the resolution of the system. For each additional bit of resolution En is cut in half, that is reduced by 6 dB.

c. Accuracy

Absolute accuracy is the maximum deviation between the actual ADC output and the ideal ADC output. The relative accuracy is the maximum deviation after gain and offset errors have been removed. The data sheet of ADC includes the relative accuracy.

d. Linearity

It is an important parameter of the accuracy of ADC. It indicates how close the ADC output is to its ideal transfer characteristics.

e. Settling Time

It is the time taken by the output of ADC to settle within a specified band ±(1/2)

LSB of its final value following a code change at the input (generally a full scale change).

f. Specifications of Sample and Hold Circuit

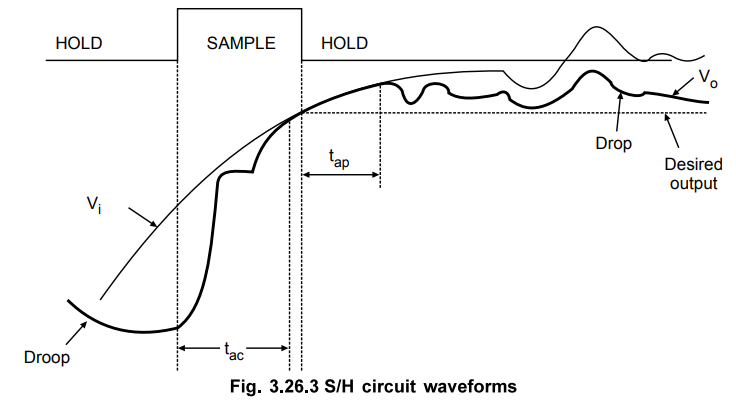
For accurate analog to digital conversion the analog input voltage should be held constant during the conversion cycle. The sample and hold circuit does this task. The specifications of sample and hold circuit are explained below with the help of waveform of sample and hold circuit. 

1. Acquisition time (t_ac)

It is the time required for the holding capacitor CH to charge up to a level close to the input voltage during sampling. It depends on three factors :

• RC time constant

• Maximum output current of op-amp

• Slew rate of op-amp

2. Aperture time (t_ap)

Because of propagation delays through the driver and switch, V_o will keep tracking V_i some time after the inception of the hold command. This is the aperture time. To get the precise timing, it is necessary to advance hold command by this amount.

3. Aperture uncertainty (Δ t_ap)

It is the variation in aperture time from sample to sample. Due to aperture uncertainty it is difficult to compensate aperture time by advancing hold command.

4. Code width

The code width is the change in input voltage that occurs between the output code transitions expressed in LSBs of full scale. Code width uncertainty is the dynamic variation or jitter in the code width causing noise.

 

Example 3.26.1 An 8-bit ADC outputs all l's when V_i -5.1 V. Find its a) Resolution and b) Digital output when V _i - 1.28 V.

Solution : a) Resolution = 2ⁿ = 2⁸ = 256 

and resolution = 5.1 V / 2⁸ – 1 = 20 mV/LSB

Therefore, we can say that to change output by 1 LSB we have to change input by 20 mV.

b) For 1.28 V analog input, digital output can be calculated as,

D = 1.28 V / 20mV / LSB = 64 LSBs

The binary equivalent of 64 is 0100 0000₂

 

Example 3.26.2 Calculate the quantizing error for 12-bit ADC with full scale input voltage 4.095 V.

Solution :

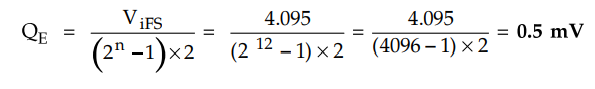
2. Basic Conversion Techniques

Analog to digital converter are classified into two general groups based on the conversion techniques. One technique involves comparing a given analog signal with the internally generated reference voltages. This group includes successive approximation, flash, delta modulated (DM), adaptive delta modulated and flash type converters. The another technique involves changing an analog signal into time or frequency and comparing these new parameters against known values. This group includes integrator converters and voltage-to-frequency converters.

In this chapter we are going to discuss following types of ADCs using various conversion techniques :

1. Single ramp or single slope

2. Dual slope

3. Successive approximation  

4. Flash

5. Delta modulation      

6. Adaptive delta modulation

a. Dual Slope ADC

Dual slope conversion is an indirect method for A/D conversion where an analog voltage and a reference voltage are converted into time periods by an integrator, and then measured by a counter. The speed of this conversion is slow but the accuracy is high.

Fig. 3.26.4 shows a typical dual slope converter circuit. It consists of integrator (ramp generator), comparator, binary counter, output latch and reference voltage. The ramp generator input is switched between the analog input voltage and a negative reference voltage, -V_REF. The analog switch is controlled by the MSB of the counter. When the MSB is a logic 0, the voltage being measured is connected to the ramp generator input. When MSB is logic 1, the negative reference voltage is connected to the ramp generator.

At time t = 0, analog switch S is connected to the analog input voltage Vp so that the analog input voltage integration begins. The output voltage of the integrator can be given as,

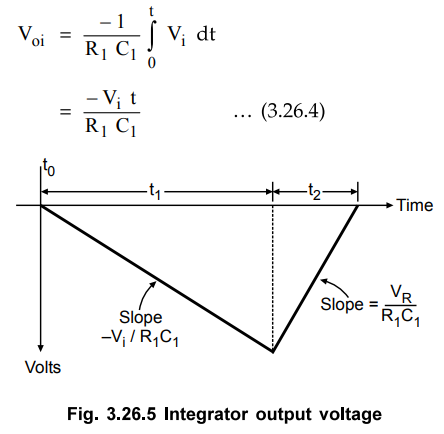
where R₁ C₁ is the integrator time constant and V is assumed constant over the integration time period. At the end of 2N clock periods MSB of the counter goes high. At a result the output of the flip-flop goes high, which causes analog switch S to be switched from V_i to -VR. At this very same time the binary counter which has gone through its entire count sequence is reset. If the clock period is T, the integration takes place for a time tF = 2ⁿ  × T. At the end of t1 the output voltage V_o is given by

V_o = V₁ = - (1 / R₁C₁) V_i t_i

The negative input voltage (-V_R) connected to the input of integrator causes the integrator output to ramp positive. When integrator output reaches zero, the comparator output voltage goes low, which disables the clock AND gate. This stops the clock pulses reaching the counter, so that the counter will be stopped at a count corresponding to the number of clock pulses in time t₂.

t₂ = Count / Clock rate  and V_l = 1/ RC (-VR)t²

The integrator output ramp down to a voltage V and get back upto 0. Therefore, the charge voltage is equal to discharge voltage and we can write,

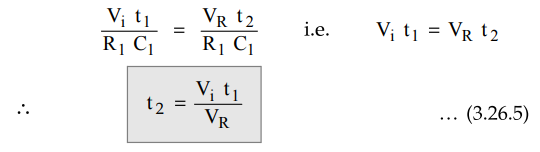
The above equation shows that t₂ is directly proportional only to the V_i since V_R and t₁ are constants. The binary digital output of the counter gives corresponding digital value for time period t₂ and hence it is also directly proportional to input signal V_i

The actual conversion of analog voltage V_in into a digital count occurs during t₂. The control circuit connects the clock to the counter at the beginning of t₂. The clock is disconnected at the end of t₂. Thus the counter contents is digital output. Hence we can write,

Digital output = (Counts / Second) t₂ … (3.26.6)

But from equation (3.26.5) we can write,

Digital output = (Counts / Second) t₁ (V_i / V_R)  … (3.26.7)

The counter output can then be connected to an appropriate digital display.

The advantages of dual slope ADC are,

1. It is highly accurate.

2. Its cost is low.

3. It is immune to temperature caused variations in R₁ and C₁.

4. It avoids the drift problem because both the integrator gain and the counting rate do not vary between two phases t₁ and t₂

The only disadvantage of this ADC is its speed which is low. 

b. Successive Approximation ADC

In this technique, the basic idea is to adjust the DAC's input code such that its output is within ± 1/ 2 LSB of the analog input V_i to be A/D converted. The code that achieves this represents the desired ADC output.

The successive approximation method uses very efficient code searching strategy called binary search. It completes searching process for n-bit conversion in just n clock periods.

Fig. 3.26.6 shows the block diagram of successive approximation A/D converter. It consists of a DAC, a comparator, and a successive approximation register (SAR).

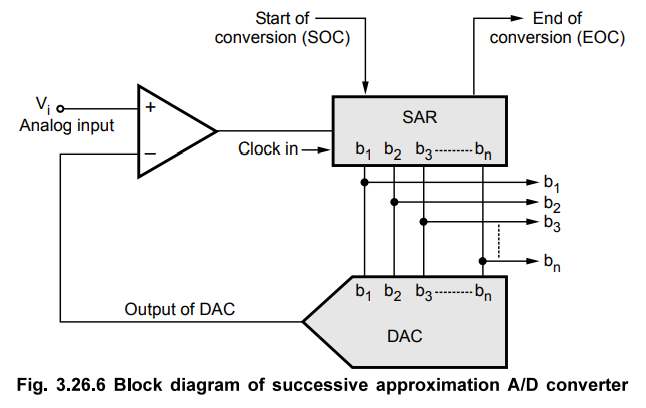
The external clock input sets the internal timing parameters. The control signal start of conversion (SOC) initiates an A/ conversion process and end of conversion signal is activated when the conversion is completed.

Operation :

The searching code process in successive approximation method is similar to weighing an unknown material with a balance scale and a set of standard weights. Let us assume that we have 1 kg, 2 kg and 4 kg weights (SAR) plus a balance scale (comparator and DAC). Now we will see the successive approximation analogy for 3-bit ADC.

Refer Fig. 3.26.6 and 3.26.7. The analog voltage V_in is applied at one input of comparator. On receiving start of conversion signal (SOC) successive approximation register sets 3-bit binary code 100₂ (b₂ =1) as an input of DAC. This is similar process of placing the unknown weight on one platform of the balance and 4 kg weight on the other. The DAC converts the digital word 100 and applies it equivalent analog output at the second input of the comparator. The comparator then compares two voltages just like comparing unknown weight with 4 kg weight with the help of balance scale. If the input voltage is greater than the analog output of DAC, successive approximation register keeps b₂ = 1 and makes b₁ = 1 (addition of 2 kg weight to have total 6 kg weight) otherwise it resets b₂ = 0 and makes b₁ = 1 (replacing 2 kg weight). The same process is repeated for b1 and bo. The status of b₀, b₁ and b₂ bits gives the digital equivalent of the analog input. Fig. 3.26.7 illustrates the process we have just discussed.

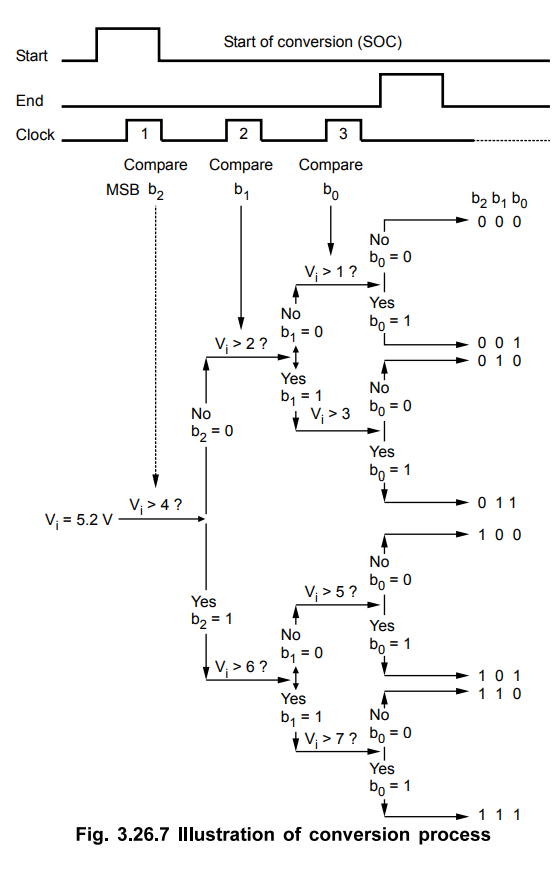
The dark lines in the Fig. 3.26.7 shows setting and resetting actions of bits for input voltage 5.2 V, on the basis of comparison. It can be seen from the Fig. 3.26.7 that one clock pulse is required for the successive approximation regsiter to compare each bit. However an additional clock pulse is usually required to reset the register prior to performing a conversion.

The time for one analog to digital conversion must depend on both the clock's period T and number of bits n. It is given as,

T_C = T (n + 1)       ...(3.26.8)

where T_C = Conversion time, T = Clock period, n = Number of bits

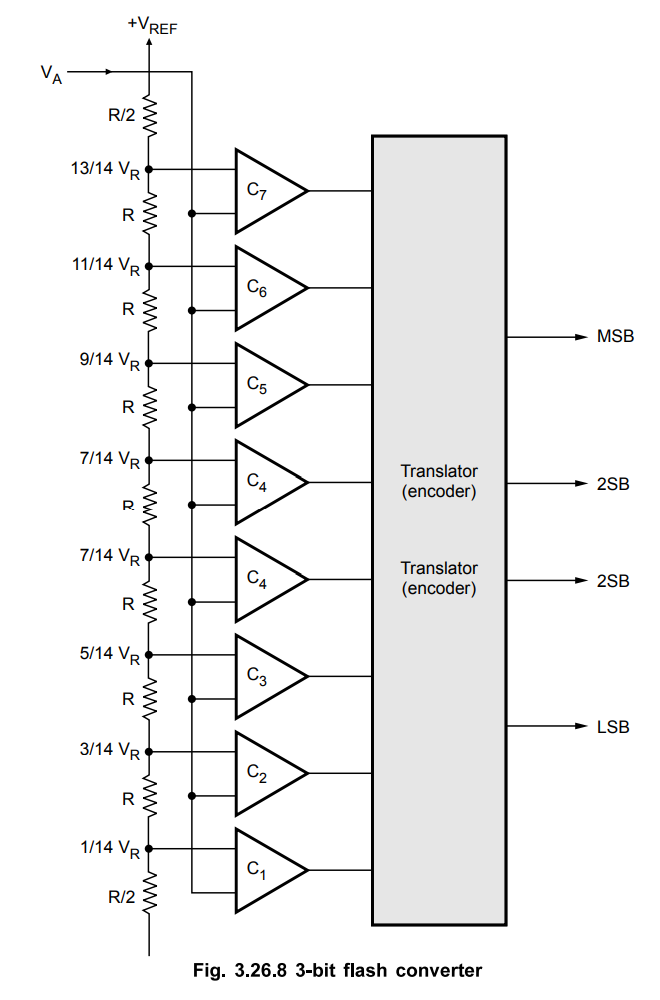
c. Flash ADC

When system designs call for the highest speed available, flash-type A/D converters (ADCs) are likely to be the right choice. They get their names from their ability to do the conversion very rapidly. Flash A/D converters, also known as a simultaneous or parallel comparator ADC, because the fast conversion speed is accomplished by providing 2ⁿ - 1 comparators and simultaneously comparing the input signal with unique reference levels spaced 1 LSB apart.

Fig. 3.26.8 shows 3-bit flash A/D converter. For this ADC, seven (2³ -1) comparators are required. As shown in the Fig. 3.26.8, one input of each comparator is connected to the input signal and other input to the reference voltage level generated by the reference voltage divider. The reference voltage (V_REF) is equal to the full scale input signal voltage. The manner in which the flash A/D converter performs a quantization is relatively simple. 

The comparators give output "1" or "0" state depending on whether the input signal is above or below the reference level at that instant. Those comparators referred above the input signal, remain tumed-off, representing a "0" state. The comparators at or below the input signal conversely become a "1" state. The code resulting from this comparator is converted to a binary code by the encoder.

The number of comparators required for n bit resolution is,

Number of comparators = 2ⁿ – 1 ... (3.26.9)

As seen earlier the quantization error is ± 2 LSB. Thus for an ADC, the maximum frequency for a sine wave to be digitised within an accuracy of ± 2 LSB is,

f_max ≅  1/ 2π(T_C)2ⁿ     ... (3.26.10)

where f_max = Maximum input frequency

T_C = Conversion time and  n = Number of bits

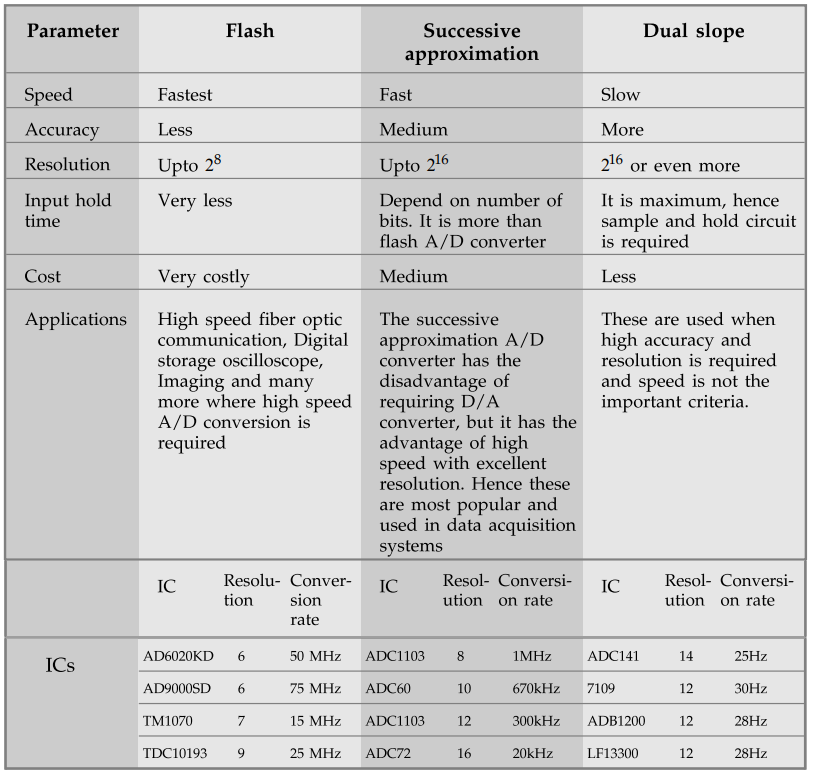
d. Comparison between Flash, Dual Slope and Successive Approximation Techniques

The comparison of ADCs is given in the tabular form as below :

 

Example 3.26.3 For a particular dual slope ADC, t₁is 83.33 ms and the reference voltage is 100 mV. Calculate t₂ if i) V_i is 100 mV and ii) 200 mV.

Solution : We know that,

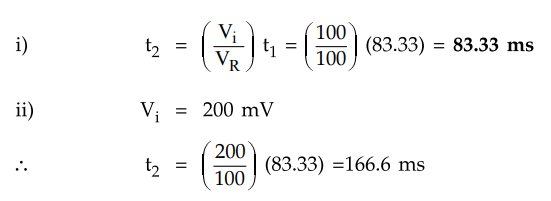
Example 3.26.4 Find the digital output of an ADC having t₁ as 83.33 ms and V_R as 100 mV for an input voltage of +100 mV. The clock frequency is 12 kHz.

Solution : The digital output is given as,

 

Example 3.26.5 An 8 bit successive approximation ADC is driven by a 1 MHz clock. Find its conversion time.

Solution :  

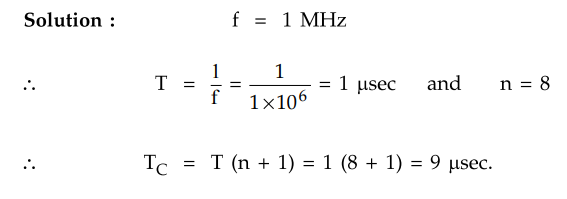
Example 3.26.6 For a particular 8-bit ADC, the conversion time is 9 μs. Find the maximum frequency of an input sine wave that can be digitized.

Solution: The maximum frequency is given by,

f_max ≈ 1 / 2π(T_C)2ⁿ ≈ 1 / 2π × 9 × 10^-6 × 2⁸ = 69.07 Hz

Example 2.26.7 A dual slope ADC uses 16-bit counter and 4 MHz clock rate. The maximum input voltage is + 10 V. The maximum integrator output voltage should be - 8 V when the counter has cycled through 2ⁿ counts. The capacitor used in the integrator is 0.1 µF . Find the value of resistor R of the integrator.

Solution :

e. Counter Type ADC

 Principle of operation :

This ADC uses DAC for A to D conversion. The output of the DAC is continuously compared with the analog input to the ADC which is to be converted into digital output. When the output of the DAC becomes greater than this analog input, the corresponding digital input to the DAC is noted which represents the analog input to the ADC.

Fig. 3.26.9 shows the circuit diagram of counter type ADC.

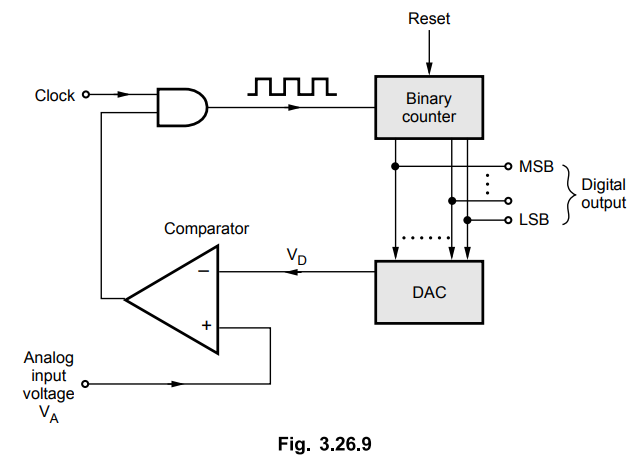
As shown in the Fig. 3.26.9, the counter type ADC consists of a binary counter, DAC, comparator and AND gate. The operation of the circuit is explained below.

i) Initially, the counter is reset, i.e. its output is set to zero by applying a reset pulse. The output of the counter is given as digital input to DAC. Since input to DAC is zero, its output V_D is zero.

ii) When the analog input voltage V_A is applied to ADC, it becomes greater than V_D - V_A acts as input voltage for non inverting terminal and V_D acts as input voltage for inverting terminal of the comparator. Since V_A is greater than V_D, the comparator output goes high.

iii) For an AND gate, one input is clock pulses and another input is the output of the comparator. Because of the high output of the comparator, the clock pulses are allowed to pass through the AND gate.

iv) The counter starts counting these close pulses. According to the number of clock pulses, the output of the counter goes on increasing. This increases the output of the DAC.

v) The above steps are continued till V_D is less than V_A.

vi) As soon as DAC output V_D becomes greater than V_A, the comparator output goes low. This disables AND gate. So the clock pulses are not allowed to pass through the AND gate. The counting process of the binary counter is stopped.

vii) The output of the binary counter which is in digital form is noted which represents the digital equivalent of the analog input voltage V_A 

viii) For the next A to D conversion, the input voltage to ADC, V_A changes. The binary counter is cleared by applying a second reset pulse and all the above steps are repeated to obtain the digital equivalent of V_A.

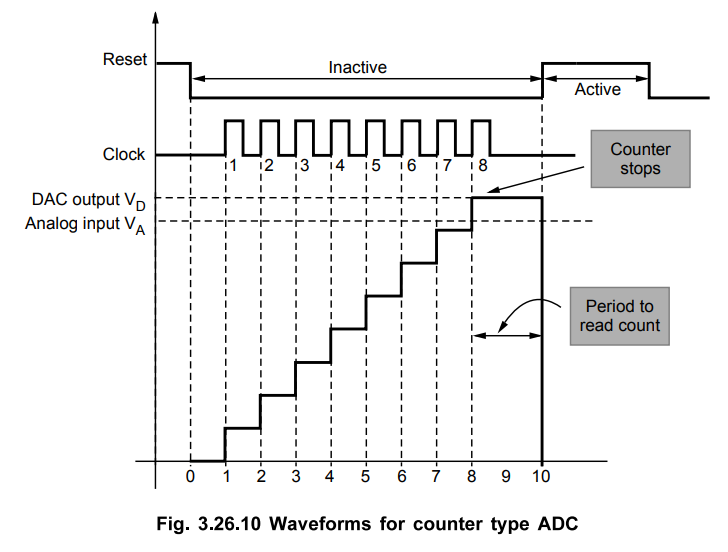
Disadvantages

It is necessary to give enough time for DAC conversion and comparator to respond. Therefore, there is a limitation on the clock frequency. As clock frequency is low, the speed of conversion is less.

Conversion time is not constant. It increases with increase in input voltage. In other words, we can say that conversion time is high at high input voltage.

Review Questions

1. Explain in detail about successive approximation ADC.

Dec.-03, 09, 12, 16, May-06, 07, 12, 16, 18, Marks 12

2. With neat diagram explain the working of dual slope type ADC.

Dec.-03, 04, 06,11, May-08, 10, 14, Marks 8

3. Explain any two techniques of converting analog to digital signal.

4. Compare the performances of various types of ADC. 

5. Explain the functions of flash type A/D converter.

6. Explain the following characteristics of ADC resolution, accuracy, settling time, linearity.

May-10, Marks 8

7. What are the advantages of continuous type A/D converter over counter type A/D converter ?

May-18, Marks 2