Adding External Resistance in Rotor Circuit

Adding External Resistance in Rotor Circuit AU : May-2000,16,18, Dec -06, 10, 13, 16

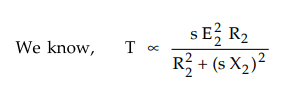
For low slip region (sX2) « R2 and can be neglected and for constant supply voltage E2 is also constant.

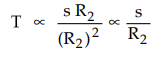
Thus if the rotor resistance is increased, the torque produced decreases. But when the load on the motor is same, motor has to supply same torque as load demands. So motor reacts by increasing its slip to compensate decrease in T due to R₂ and maintains the load torque constant. So due to additional rotor resistance R₂ , motor slip increases i.e. the speed of the motor decreases. Thus by increasing the rotor resistance R₂ , speeds below normal value can be achieved. 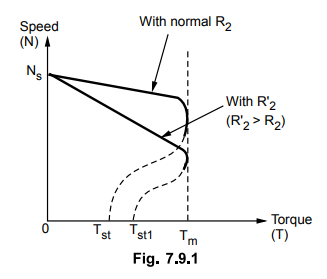Another advantage of this method is that the starting torque of the motor increases proportional to rotor resistance.

The Fig. 7.9.1 shows the torque-speed curves for rotor resistance control.

But this method has following disadvantages :

1. The large speed changes are not possible. This is because for large speed change, large resistance is required to be introduced in rotor which causes large rotor copper loss to reduce the efficiency.

2. The method can not be used for the squirrel cage induction motors.

3. The speeds above the normal values can not be obtained.

4. Large power losses occur due to large I R loss.

5. Sufficient cooling arrangements are required which make the external rheostats bulky and expensive.

6. Due to large power losses, efficiency is low.

Thus the method is rarely used in the practice. 

Example 7.9.1 The rotor of a 4-pole, 50 Hz slip ring IM has a resistance of 0.25 Ω per phase, rotor standstill reactance of 2 Ω and runs at 1440 r.p.m. at full load. Calculate the external resistance per phase which must be added to lower the speed at 1200 r.p.m., the torque being the same as before.

Solution :

P = 4, f = 50 Hz, R₂ = 0.25 Ω, Nj = 1440 r.p.m., N2 = 1200 r.p.m., X₂ = 2 Ω

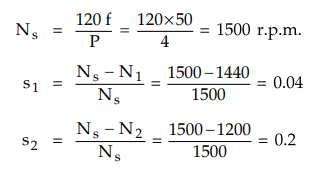
Now let R_x be the external resistance added so that R₂ = R_x + R₂ for N₂ = 1200 r.p.m.

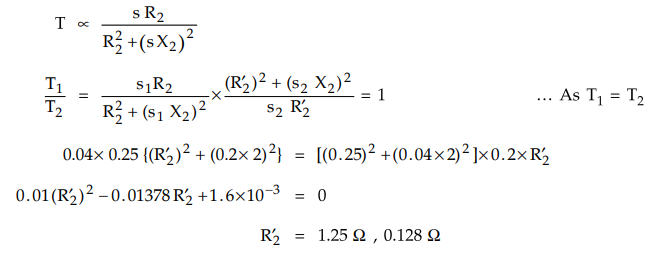
But R₂ cannot be less than R₂ hence R₂ =1.25 Ω

R_x = R₂ – R₂ = 1.25 - 0.25 = 1 Ω

Example 7.9.2 A 4-pole, 3-phase, 50 Hz , slip ring type induction motor has a rotor resistance of 0.25 Ω per phase and rotor reactance of 2 Ω per phase at standstill condition. It is running at 1455 r.p.m. speed. Calculate the value of external resistance per phase required in the rotor circuit to reduce the speed by 17 %. Assume load torque constant.

Solution :

P = 4, f = 50 Hz, R₂ = 0.25 Ω, X₂ = 2 Ω,    N₁ = 1455 r.p.m.

Neglecting lower value as less than R₂.

R₂ = R₂ + R_ex = 1.6124 Ω

R_ex = 1.6124 - 0.25 = 1.3625 Ω

This is the extra resistance per phase required in the rotor.

Examples for Practice

Example 7.9.3 A 4-pole, 50 Hz, 3 phase induction motor has rotor resistance of 0.2 Ω per phase and rotor standstill reactance of 1 Ω per phase. On full load it is running with a slip of 4 %. Calculate the extra resistance required in the rotor circuit per phase to reduce the speed to 1260 r.p.m., on the same load condition.

[Ans.: 0.6 Ω per phase]

Example 7.9.4 A 3 phase, 6 pole, 50 Hz induction motor when fully loaded with a slip of 3 %. Find the value of the resistance necessary in series per phase of the rotor to reduce the speed by 10 %. Assume rotor resistance per phase is 0.2 Ω AU : May-2000

[Ans.: 0.65 Ω]

Review Questions

1. Explain the rotor rheostat speed control of three phase slip ring induction motor. AU : Dec.-06, 10, 13, Marks 8

2. Explain in detail the speed control methods of induction motor. AU ; May-16, Marks 8

3. Explain the speed control methods cf a three phase induction motor. AU ; Dec.-16,May-18, Marks 16