Additional solved problems

ADDITIONAL SOLVED PROBLEMS

 

1. Determine the power consumed by 10Ω resistor in the circuit shown in the figure below.

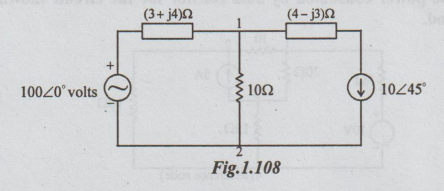
Solution:

There are two nodes. Node 2 is taken as reference, Let the voltage of node 1 be V₁. The nodal equation is

 

2. Determine the power consumed by 20 Ω resistor for the circuit shown by using nodal voltage method.

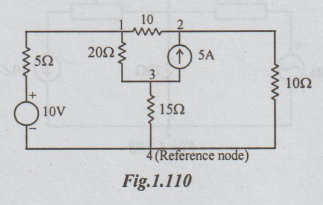
Solution: Let V₁, V₂ and V₃ be the voltages of the nodes 1, 2 and 3 respectively.

By inspection,

V₁ = Δ₁ / Δ

=  0.0553 / 6.52 × 10^-3

= 8.48 volts

V3 = Δ₃ / Δ

= -0.255 / 6.52 × 10^-3 = -39.11 volts

Voltage across 20 Ω = V₂₀ = V₁ ~ V₃

= 47.59 volts

I₂₀ = 47.59 / 20 = 2.38A

Power consumed by 20Ω = I²R

= (2.38)² × 20

= 113.3 W

 

3. Using node voltage method, determine the voltage across the 4Ω resistor.

Solution: Here, the voltage source is an ideal one. Hence we cannot solve by writing the matrix.

Let the node 5 be the reference one.

i.e., V₅ = 0

So, V₄ = + 12 volts

Let V₁, V₂ and V₃ be the voltages of the nodes 1, 2 and 3 respectively.

Applying KCL at node 1, we get,

V₁ - V₃ / 4 + V₁ - V₂ / 6 +  2 + 3 = 0

⇒V₁ - V₃ /4 + V₁ - V₂ / 6 + 5 = 0

3 (V₁ - V₃) + 2 (V₁ - V₂) + 60 = 0

5V₁ - 2V₂ - 3V₃ = -60

10V₁ - 4V₂ - 6V₃ = -120 ..(1)

Applying KCL at node 2, we get,

V₂ -  V₄ / 3 +  V₂-V₁ / 6 – 2 =0

 3 (V₂ - V₄) + (V₂-V₁) =  12

or 3 (V₂-I₂) + (V₂-V₁) = 12

or -V₁ +4V₂ = 48 ...(2)

Similarly application of KCL at node 3 yields to

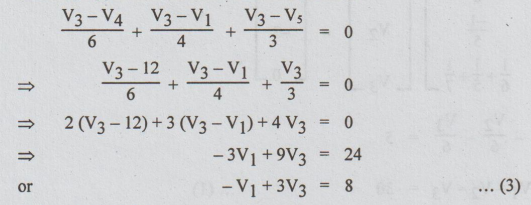
2 (V₃ – 12) + 3(V₃-V₁)+4 V₃ = 0

-3V₁ + 9V₃ = 24

-V₁ + 3V₃ = 8 ...(3)

Adding (1) and (2), we get

9V₁ - 6V₃ = - 72...(4)

 (3) × 9+ (4)

21V₃ = 0

V₃ = 0

From (3) V₁ = -8

Current through 4Ω = V₃ - V₁/4

= 0- ( -8) / 4

=2A

 

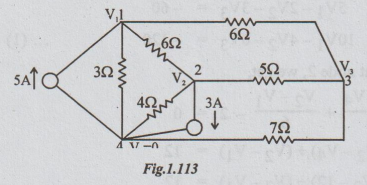
4. For the network of the following figure, write the nodal equations and solve for the nodal voltages.

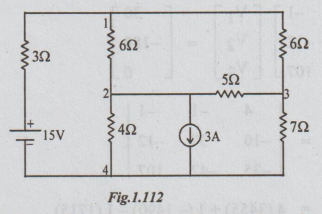
Solution: Let the nodes be numbered as shown. Convert the voltage source into equivalent current source.

By inspection we can write that,

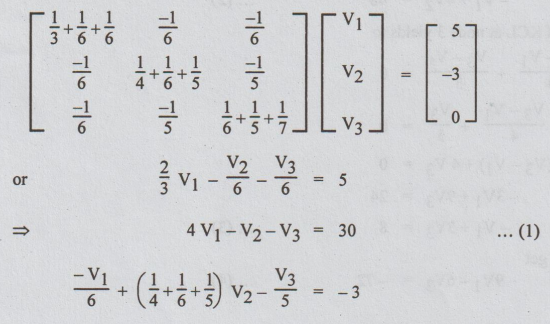
4 V₁ - V₂ - V₃ = 30....(1)

-V₁ / 6 + (1/4 + 1/6 + 1/5 ) V₂ - V₃/5 = -3

⇒ -10V₁ + (15 + 10 + 12) V₂-12V₃ = - 180

or -10V₁+ 37V₂ - 12V₃ = - 180...(2)

and -V₁ / 6 – V₂ /5 + 107/210 V₃ = 0

= -35V₁ - 42V₂ + 107V₃ = 0 ...(3)

Putting the equations (1), (2) and (3) in matrix form,

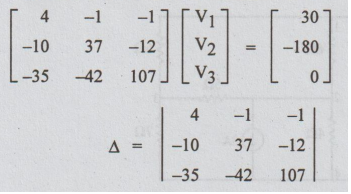
= 4 (3455)+1 (-1490) - 1 (1715)

= 10615

 

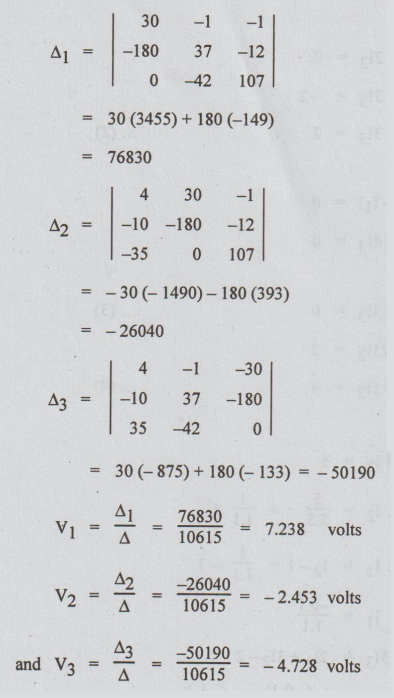
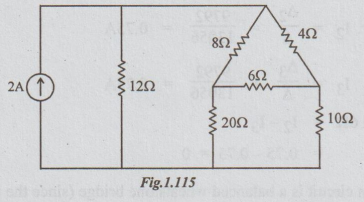
5. For the circuit given below, use loop analysis, to determine the two loop currents I₁ and I₃.

 

5. Use loop current analysis and find current through 62 resistor of the network.

Solution:

First convert the current source into its equivalent voltage source.

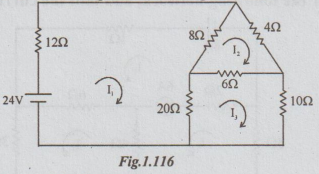
Let the loop currents be as shown. By inspection,

Note: The given circuit is a balanced wheatstone bridge (since the product of opposite arms is equal). Hence the current in 6 Ω must be zero.

 

6. Write loop equations for the following network, and find the current supplied by 8V source.

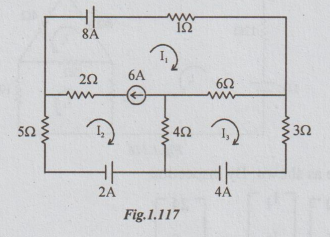
Solution:

Let the loop currents be as shown in the figure.

The current through 8V source = I₁

I₁ – I₂ = 6 … (1)

 

1. Dependent Sources (Controlled Sources): Loop analysis:

Case (i): Current-controlled voltage sources:

The loop equations may be written in the same manner as for the circuits with independent voltage sources. However, there will be an additional equation giving relationship between the source voltage and the controlling quantity.

 

Example 1 Determine the current through 42 resistor of the network shown.

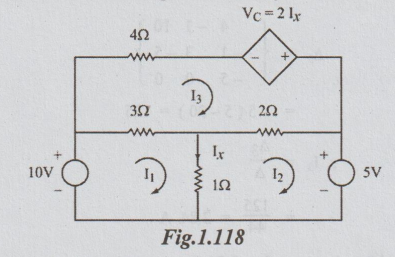
Solution: Let the loop currents be as shown.

Vc = 21x (given)

But Ix = I₁ – I₂

So, = Vc 2 (I₁ – I₂)

Now, by inspection we write that

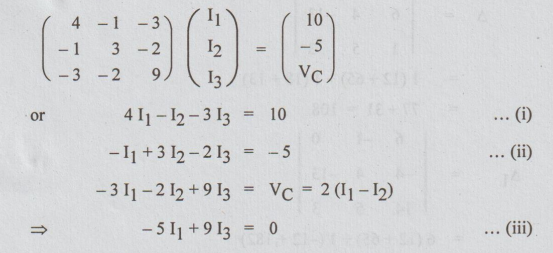
Again putting the equations (i), (ii) and (iii) in the matrix form, we get

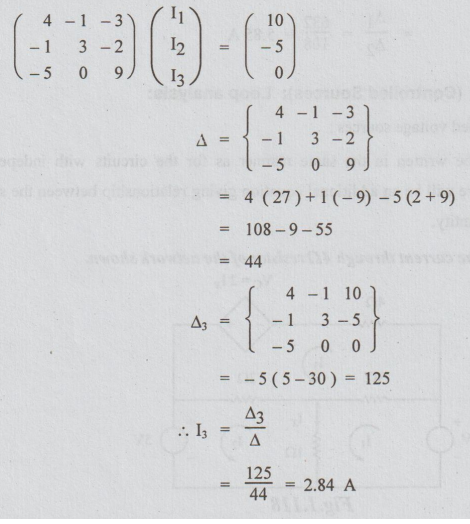
Current through 4 Ω resistor I₃ = 2.84 A

Case (ii): (Voltage-controlled current source):

Loop equations can be written in the same manner as for the circuits with independent sources except for the fact that there will be an additional equation giving the relationship between the source current and the controlling quantity.

 

Example 2 Determine the current through the 100V source in the figure.

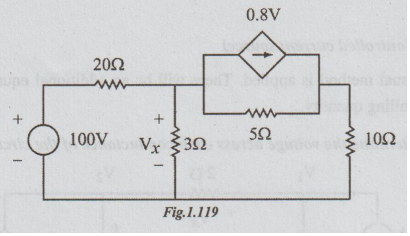
Solution:

Step 1: In the circuit given, the controlled source is voltage controlled current source. First let us convert it into equivalent voltage source and draw the circuit as below.

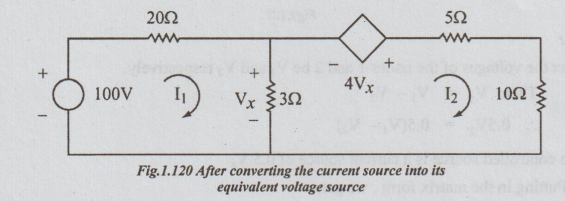
Step 2: Let I, and I2 be the loop currents as shown in the figure.

V_x = 3 (I₁ – I₂)

4 V_x = 12 (I₁ – I₂)

Step 3: Putting in the matrix form we get,