Alternative Expression for Power Developed by a Synchronous Motor

Alternative Expression for Power Developed by a Synchronous Motor

Consider the phasor diagram of a synchronous motor running on leading power factor cos as shown in the Fig. 4.14.1.

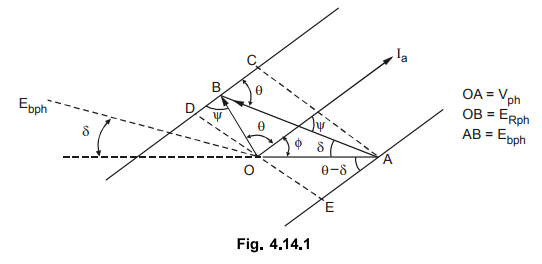
The line CD is drawn at an angle θ to AB.

The lines AC and DE are perpendicular to CD and AE. 

OB = E_Rph - I_aZ_s and ∠ OBD = ψ

and angle between AB = E_bph and I_aph is also ψ

The mechanical per phase power developed is given by,

P_m = E_bph I_aph cos (E_bph ^ I_aph)

= E_bph I_aph cos (ψ)    … (4.14.1)

In triangle OBD,

BD = OB cos ψ =  I_aZ_s cos I_aZ_s

OD = OB sin v = Ia Zs sin ψ

Now  BD = CD - BC = AE - BC

AE = OA cos (θ - δ ) = V_ph cos (θ - δ )  … (4.14.2),

Substituting in equation (4.14.2),

I_aZ_s cos ψ = V_ph cos (θ - δ )  - E_b cos θ

I_a cos ψ = V_ph / Z_S cos (θ - δ )  - E_b / Z_S cos θ       … (4.14.3)

All values are per phase values

Substituting equation (4.14.3) in equation (4.14.1),

This is the expression for the mechanical power developed angle interms of the load angle δ and the internal machine angle θ, for constant voltage V_ph and constant E_b i.e. excitation.

 

1. Condition for Maximum Power Developed

The value of δ for which the mechanical power developed is maximum can be obtained as,

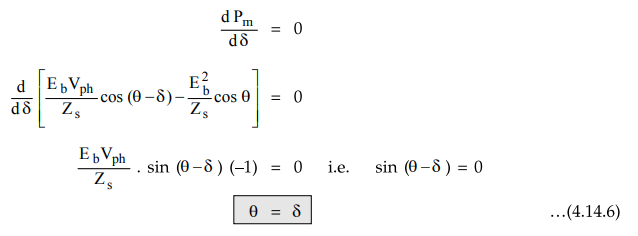
Key Point Thus when Ra is negligible, θ = 90^o for maximum power developed. The corresponding torque is called pull out torque.

a.  The Value of Maximum Power Developed

The value of maximum power developed can be obtained by substituting the equation of P_m

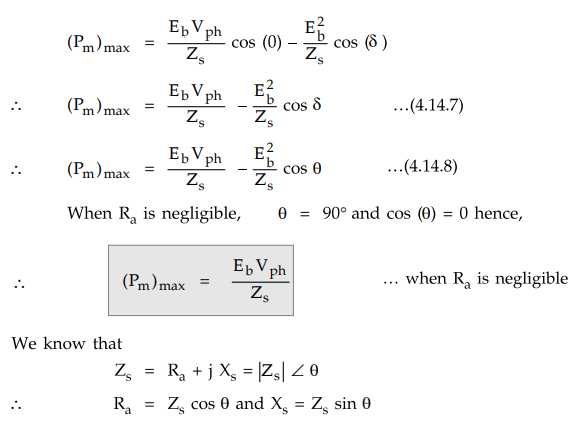
Substituting cos θ = R_a/Z_s, in equation (4.14.8) we get,

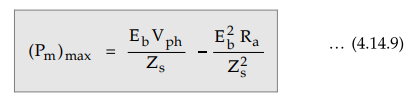
Solving the above quadratic in E_b we get,

As E is completely dependent on excitation, the equation (4.14.10) gives the excitation limits for any load for a synchronous motor. If the excitation exceeds this limit, the motor falls out of step.

The torque is given by P/ hence the maximum torque developed by a synchronous motor is,

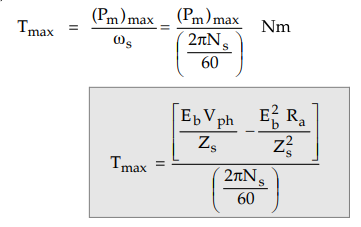
b. Condition for Excitation When Motor Develops (P_m) max

Let us find excitation condition for maximum power developed. The excitation controls E_b. Hence the condition of excitation can be obtained as,

This is the required condition of excitation.

Key Point Note that this is not maximum value of E_b but this is the value of Eb for which power developed is maximum.

The corresponding value of maximum power is,

 

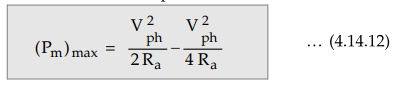
Example 4.14.1 The excitation of 415 V, 3 phase, mesh connected synchronous motor is such that the induced e.mf. is 520 V. The impedance per phase is 0.5 + j 4 Ω. If the friction and iron losses are constant and equal to 1000 watts, calculate HP output, line current, power factor and the efficiency for maximum power output.

Solution : The given values are,

 

Example 4.14.2 A 2500 V, 3 phase, star-connected motor has a synchronous reactance of 5 Ω per phase. The motor input is 1000 kW at rated voltage and an excitation e.mf. of 3600 V (line). Calculate the line current and power factor.

Solution :

 

Example 4.14.3 A 3000 V, 3 phase synchronous motor running at 1500 r.p.m. has its excitation kept constant coresponding to no-load terminal voltage of 3000 V. Determine the power input, power factor and torque developed for an armature current of 250 A if the synchronous reactance is 5 Q per phase and armature resistance is neglected. AU : May.-06, Marks 9

Solution :

 

Example 4.14.4 A 4 pole, 400 V, 50 Hz, 3 phase star connected synchronous motor has a synchronous reactance of 2 Ω per phase. The resistance of the stator winding is negligible. The field excitation is so adjusted that the e.m.f. induced is equal to the supply voltage. In application of a certain load the rotor is retarded by 4 mechanical degrees. Find the armature current drawn by the motor.

Solution :

 

Example 4.14.5 A 400 V, 6 pole, 3 phase, 50 Hz, star connected synchronous motor has stator resistance and synchronous reactance of 0.2 ohm and 3.0 ohm per phase respectively. It takes 20 Amps at u.p.f. when operating with a certain field current. If the load torque is increased until the current is 60 A, the field current remaining the same, find the gross torque developed and the power factor.

Solution : The given values are,

 

Example 4.14.6 A 500 hp, 720 rpm synchronous motor connected to a 3980 V, 3 phase line generates an excitation voltage E_b of 1790 V (line to neutral) when the dc exciting current is 25 A. The synchronous reactance is 22 Ω and the torque angle between Eb and E is 30°, calculate.

1) The value ofEx.

2) The ac line current.

3) The power factor of the motor.

4) The approximate horsepower developed by the motor.

5) The approximate torque developed at the shaft.  AU : May-17, Marks 8

Solution :

 

Example 4.14.7 A 3 phase, 3300 V, star connected synchronous motor has an effective resistance and synchronous reactance of 2.0 Ω and 18.0 Ω per phase respectively. If the open circuit generated e.m.f. is 3800 V between lines, calculate,

i) The maximum total mechanical power that the motor can develop and

ii) The current and power factor at the maximum mechanical power.

Solution :

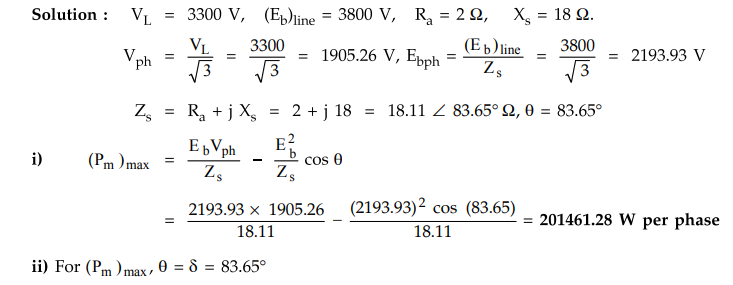
Consider the phasor diagram shown in the Fig. 4.14.7.

As E_b > V, I_a leads V. Applying cosine rule to triangle OAB we can write,

 

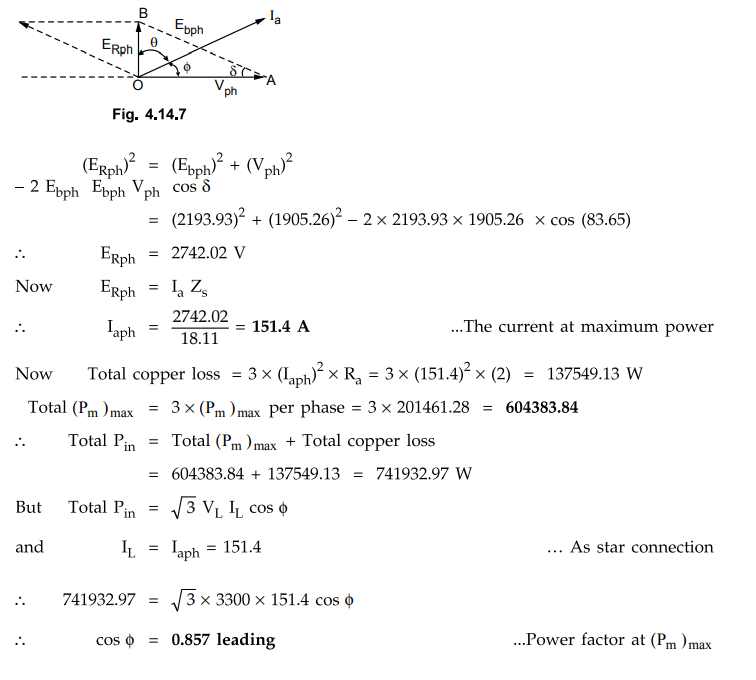
Example 4.14.8 A 6600 V, star-connected, three phase synchronous motor works at constant voltage and constant excitation. Its synchronous impedance is ((2.0 + j20.0) 2/phase.) When the input is 1000 kW, the power factor is 0.8 leading. Find the power factor when the input is increased to 1500 kW.

Solution :

V_L = 6600 V, Z_S = 2 + j 20 Ω,  P₁ = 1000 kW, P₂ = 1500 kW

As excitation is constant, Ebph remains constant though P₁ increases to P₂ = 1500 kW. Let new armature current be I_a2ph and p.f. as cos ϕ₂.

 

Example 4.14.9 A 1000 kW, 3 phase star connected 3.3 kV, 24 pole, 50 Hz synchronous motor has a synchronous reactance of 3.24 Ω. per phase and resistance is negligible. The motor is fed from infinite busbars. Its field excitation is adjusted to result in UPF at read load. Compute the maximum power and torque that the motor can deliver with its excitation remaining constant at this value.

Solution :

 

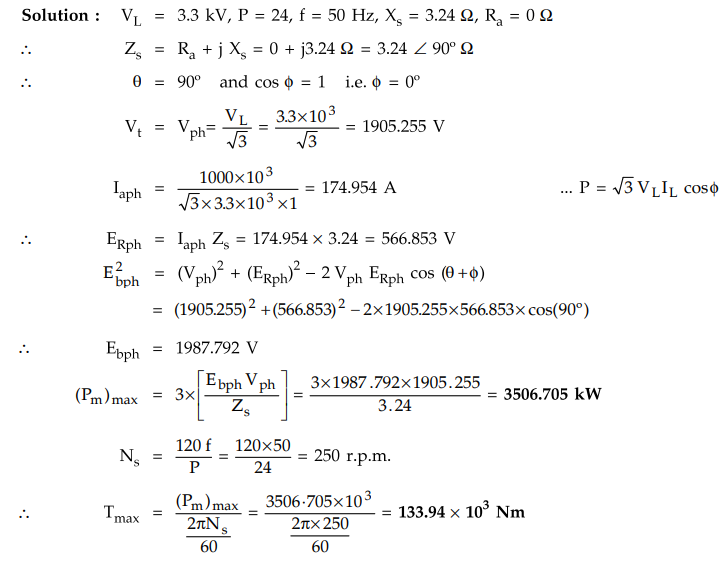
Example 4.14.10 A 1000 kVA, 11000 V, 3 phase, star connected synchronous motor has armature resistance and reactance of 3.5 Ω and 40 Ω per phase respectively. Determine induced e.m.f. and angular retardation of the rotor when fully loaded at i) Unity ii) 0.8 p.f. lagging iii) 0.8. p.f. leading.  AU : Dec.-15, May-17, Marks

Solution :

 

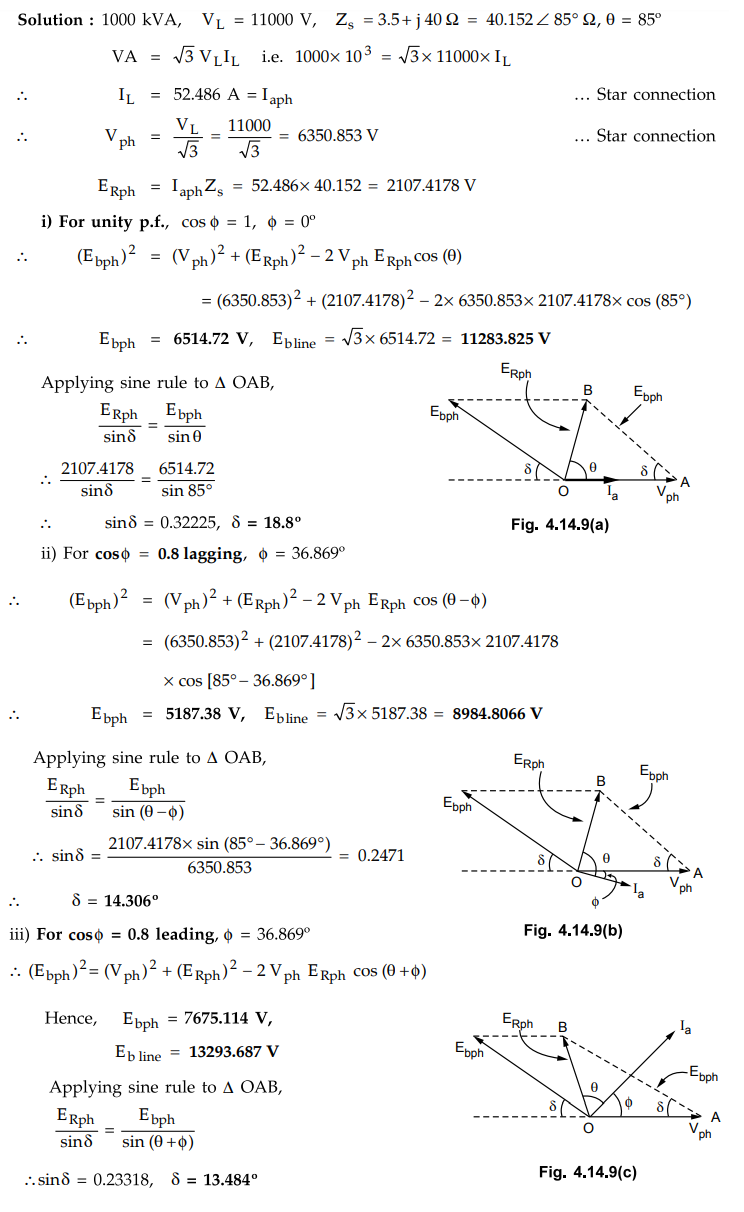
Example 4.14.11 A 6 pole, 3 phase, star connected synchronous motor has synchronous impedance of (0.5 + j 8.0) Ω per phase. When operating on 2.2 kV, 50 Hz bus bars, its field current is such that the induced e.m.f. is 1.8 kV. Calculate the maximum torque that can be developed at this excitation condition AU : May-13, Marks 8

Solution :

 

Example 4.14.12 The synchronous reactance per phase of a 3-phase, star connected 6600 V synchronous motor is 20 Ω. For a certain load the input is 900 kW at normal voltage and the induced line e.m.f. is 8500 V. Determine the line current and power factor.   AU : Dec-13, Marks 16

Solution :

Refer Ex. 4.14.2 for the procedure and verify the answer as : I_a = 89.1731 A, cos ϕ = 0.8828 leading.

 ppppppppppppppppppppppppppp

Example 4.14.13 A 75 kW, three-phase Y - connected 50 Hz, 440 V, cylindrical rotor synchronous motor operates at rated condition with 0.8 pf leading. The motor efficiency excluding field and stator losses is 95 % and X3 = 2.5 2. Calculate :

i) Mechanical power developed

ii) Armature current

iii) Back emf

iv) Power angle

v) Maximum or pull out torque of the motor.

AU : May-18, Marks 13

Solution :

 

Examples for Practice

Example 4.14.14 A 15 kW, 400 V, 50 Hz, 3 phase star connected synchronous motor with impedance of (1 + j 5.0) Ω /phase is working at rated voltage and rated frequency. Find the load angle, armature current and power factor when the excitation is adjusted to 480 V.

[Ans.: 8 =24.9°, 23.2284 A, 0.932 leading] 

Example 4.14.15 A 400 V, 50 Hz, 6-pole, three phase, start connected synchronous motors has X_s = 4 ohm/ph and R_a = 0.5 ohm/ph. On full load the excitation is adjusted so that the machines takes an armature current of 60 A at 0.866 pf. leading. Find the maximum power output if the total power losses are 2 kW and excitation same.

[Ans.: Net maximum output = 51.3827 kW]

Example 4.14.16 A 400 V, 7.5 hp, 3 ph, synchronous motor has negligible armature resistance and a synchronous reactance of 10 Ω /ph. Determine the minimum current and the corresponding e.m.f. for full load condition. Assume a motor efficiency of 85%.

[Ans.: 9.367 A, 249.2135 V]

Example 4.14.17 A 20 MVA, 11 kV, 3-phase, delta-connected synchronous motor has a synchronous impedance of 15 ohm/phase. Windage, friction and iron losses amount to 1200 kW.

i) Find the value of unity power factor current drawn by the motor at a shaft load of 15 MW. What is the excitation emf under this condition ?

ii) If the excitation emf is adjusted to 15.5 kV (line) and the shaft load is adjusted so that the motor draws unity power factor current find the net motor output.

[Ans.: i) 850.28 A, 13.23 kV, ii) 22.824 MW]

Review Questions

1. Derive an expression for power delivered by a synchronous motor in terms of a load angle AU : May-09, 13, 17, Dec.-15, Marks 8

2. Write a note on the effect of torque angle on power developed by a synchronous motor. AU : Dec.-09, Marks 8

3. Derive an expression for the maximum torque developed per phase of a synchronous motor. AU : May-12, Marks 8

4. Derive the condition for maximum power and the value of maximum power for synchronous motor. AU : May-13, Marks 6