Ampere's Circuital Law

Ampere's Circuital Law

AU ; Dec.-03, 10, 13, May-10, 17

• In electrostatics, the Gauss's law is useful to obtain the  in case of complex problems. Similarly in the magnetostatics, the complex problems can be solved using a law called Ampere's circuital law or Ampere's work law.

• The Ampere's circuital law states that,

• The line integral of magnetic field intensity   around a closed path is exactly equal to the direct current enclosed by that path.

• The mathematical representation of Ampere's circuital law is,

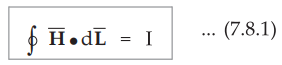
• The law is very helpful to determine   when the current distribution is symmetrical.

1. Proof of Ampere's Circuital Law

• Consider a long straight conductor carrying direct current I placed along z axis as shown in the Fig. 7.8.1. 

Consider a closed circular path of radius r which encloses the straight conductor carrying direct current I. The point P is at a perpendicular distance r from the conductor. Consider   at point P which is in ā ϕ direction, tangential to circular path at point P.

While  obtained at point P, from Biot-Savart law due to infinitely long conductor is,

• This proves that the integral 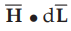 along the closed path gives the direct current enclosed by that closed path.

Key Point : The path enclosing the direct current I need not be a circular and it may be any irregular shape. The law does not depend on the shape of the path but the path must enclose the direct current once. This path selected is called Amperian path similar to the Gaussian surface used while applying Gauss's law.

2. Steps to Apply Ampere's Circuital Law

• Follow the steps given to apply Ampere's circuital law :

Step 1 : Consider a closed path preferrably symmetrical such that it encloses the direct current I once. This is Amperian path.

Step 2 : Consider differential length   depending upon the co-ordinate system used.

Step 3 : Identify the symmetry and find in which direction exists according to the co-ordinate system used.

Step 4 : Find 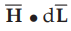  the dot product. Make sure that  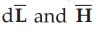in same direction.

Step 5 : Find the integral of 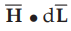 around the closed path assumed. And equate it to current I enclosed by the path.

• Solving this for the   we get the required magnetic field intensity due to the direct current I.

• To apply Ampere's circuital law the following conditions must be satisfied,

1. The   is either tangential or normal to the path, at each point of the closed path.

2. The magnitude of   must be same at all points of the path where H is tangential.

• Thus identifying symmetry and identifying the components of    present, plays an important role while applying the Ampere's circuital law.

Review Question

1. State and explain Ampere's circuital law using mathematical expressions for finding magnetic flux density due to current I.

AU : Dec.-03, 10, 13, May-10, 17, Marks 8