An Electric Dipole

An Electric Dipole

• The two point charges of equal magnitude but opposite sign, seperated by a very small distance give rise to an electric dipole. The field produced by such a dipole plays an important role in the engineering electromagnetics.

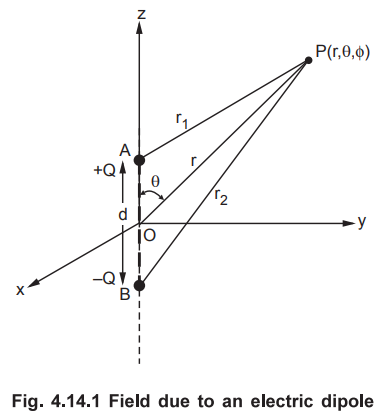
 • Consider an electric dipole as shown in the Fig. 4.14.1. The two point charges + Q and - Q are separated by a very small distance d.

• Consider a point P (r, θ, ϕ) in spherical coordinate system. It is required to find  due to an electric dipole at point P. Let O be the midpoint of AB. The distance of point P from A is r₁ while the distance of point P from B is r₂. The distance of point P from point O is r. The distance of separation of charges i.e. d is very small compared to the distances r₁,r₂ and r. The coordinates of A are (0,0, + d/2) and that of B are (0,0, - d/2).

• To find , we will find out the potential V at point P, due to an electric dipole. Then using , we can find  due to an electric dipole. 

1. Expression of  due to an Electric Dipole

In spherical coordinates, the potential at point P due to the charge + Q is given by,

V₁ = +Q / 4πƐ₀r₁ … (4.14.1)

• The potential at P due to the charge - Q is given by,

V₂ = -Q / 4πƐ₀r₂ … (4.14.2)

• The total potential at point P is the algebraic sum of V₁ and V₂.

• If now point P is located in z = 0 plane as shown in the Fig. 4.14.2, then r₂ = r₁ . Hence we get V = 0. Thus the entire z = 0 plane i.e. xy plane is a zero potential surface.

• All points in z = 0 plane behave similar to the points at infinity as all are at zero potential.

• Now consider that P is located far away from the electric dipole. Thus r₁, r₂ and r can be assumed to be parallel to each other as shown in the Fig. 4.14.3.

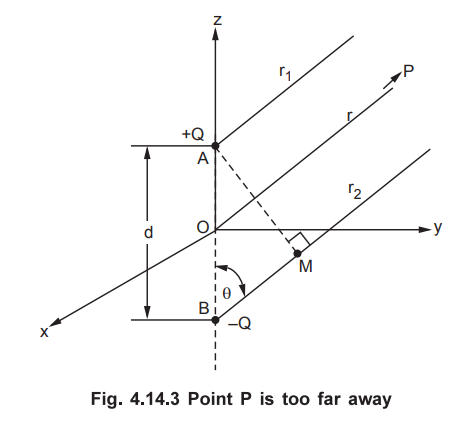
• AM is drawn perpendicular from A on r₂. The angle made by r₁, r₂ and r with z axis is θ as all are parallel.

This is electric field  at point P due to an electric dipole.

2. Dipole Moment

Let the vector length directed from - Q to + Q i.e. from B to A is 

Its component along   direction can be obtained as,

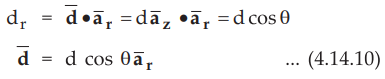
Then the product Q is called dipole moment and denoted as 

The dipole moment is measured in Cm

(coulomb-metre).

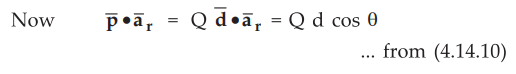
... from (4.14.10)

Hence the expression of potential V can be expressed as,

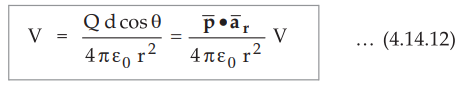
Note that,

•   = Unit vector in the direction of distance vector joining the point at which moment exists and point at which V is to be obtained.

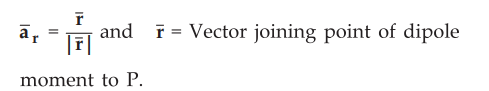
• It can be noted that the dipole moment and potential will remain same though Q increases and d decreases or viceversa, as long as the product of Q and d remains constant.

• Now if 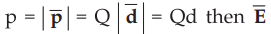 due to a dipole can be expressed interms of magnitude of dipole moment as,

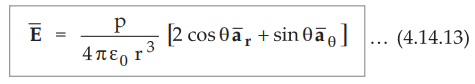
Observe that,

1. The potential is inversely proportional to the square of the distance from dipole.

2. The electric field is inversely proportional to the cube of the distance from dipole.

• A single point charge is called monopole in which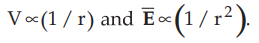 

• The arrangement of two point charges is called dipole in which 

• Similarly symmetrical arrangements of larger

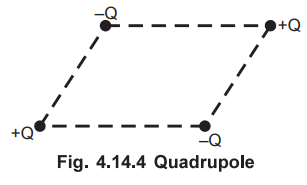
number of point charges produce potentials and fields which are inversely proportional to the higher powers of r, such as r³,r⁴... etc. Such arrangements are called multipoles. The symmetrical arrangement consisting of two dipoles as shown in the Fig. 4.14.4 is called quadrupole. The symmetric arrangement consisting of two quadrupoles is called octupole and so on.

Ex. 4.14.1 A dipole having moment

is located at Q(l,2,-4) in free space. Find V at P(2,3,4).

Sol. : The potential V in terms of dipole moment is,

Ex. 4.14.2 Two point charges, 1.5 nC at (0, 0, 0.1) and - 1.5 nC at (0, 0, - 0.1), are in free space. Treat the two charges as a dipole at the origin and find potential at P(0.3, 0, 0.4).

Sol . :

The dipole is shown in the Fig. 4.14.5.

Examples for Practice

Ex. 4.14.3 What is the electric field at (x = 0, y = 0, z = 5) m due to a pure dipole 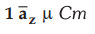 at the origin ?

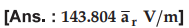
Ex. 4.14.4 Point charges of + 3 µC and - 3 µC are located at (0, 0, 1) mm and (0, 0, -1) mm respectively in free space.

i) Find dipole moment   ?

ii) Find   in spherical components at

P (r = 2, θ = 40°, ϕ = 50°) ?

Ex. 4.14.5 An electric dipole located at the origin in the free space has a moment

i) Find V at (2, 3, 4) ii) Find V at r = 2.5,

θ = 30°, ϕ = 40°

[Ans.: i) 0.2302 V, ii) 1.9734 V]

Review Question

1. Explain electric dipole. Derive the expression for the electric field intensity and potential due to an electric dipole at any point P.

AU : May-17, Marks 8