Analog Multiplier IC

Analog Multiplier IC

The multiplier integrated circuit is commonly used in practice to perform various mathematical operations.

Monolithic Integration has lowered the cost of multiplier ICs considerably. Such an IC is not only useful as multiplier but can be used as a simple and direct solution to complex signal processing problems. Such ICs can be configured to use in many applications as signal multiplications in process instrumentation, chemical analyzers, servo mechanism control systems, frequency doublers, phase angle detectors, true r.m.s. converter, controlling of oscillator frequency and so on. The ICs can be used to improve the data acquisition through ratioing two signals. Let us study first a basic multiplier IC and its characteristics.

 

1. Basic Multiplier and its Characteristics

A basic multiplier is an active circuit in which the output voltage is proportional to the product of the two input signals. A schematic symbol of such basic multiplier IC is shown in the Fig. 4.8.1.

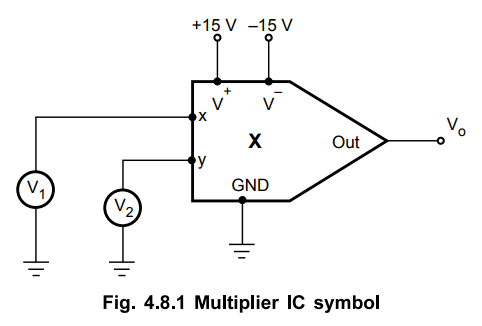
The terminals V⁺ and V^- are supply terminals for IC where dual supply is to be connected, generally ± 15 V as shown. The x and y are the two input terminals where two inputs V₁ and V₂ are connected.

The output of such basic multiplier is

V_o = K V₁ V₂   ... (4.8.1)

where K is constant and is equal to 1 / V_ref Usually V_ref is set to 10 V internally and hence,

V_o = V₁ V₂   / 10  ... (4.8.2)

As long as it is ensured that both the input voltages are below the reference voltage, (V₁ V₂   < V_ref ), the output of the basic multiplier will not saturate. 

Depending on the use of the basic multiplier, it is necessary to restrict the polarity of one or both the inputs. Depending upon the polarity restriction, the IC operation is called as,

i) One quadrant multiplier : In such operation, the polarities of both the inputs must always be positive.

ii) Two quadrant multiplier : A two quadrant multiplier functions properly if one input is held positive and the other is allowed to swing in both positive and negative.

iii) Four quadrant multiplier : If both the inputs are allowed to swing in both positive and negative directions, the operation is four quadrant multiplier operation.

These operations are shown in the Fig. 4.8.2.

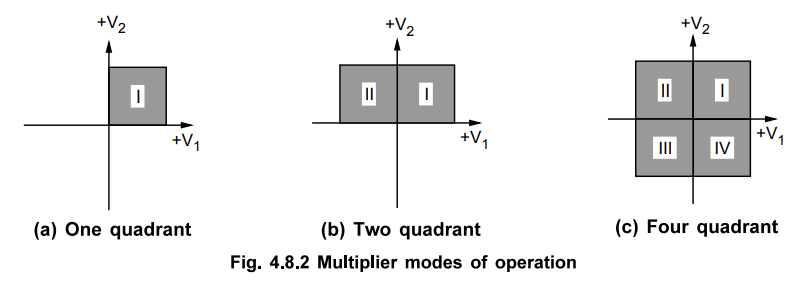
Performance Parameters of Multiplier

Let us define the performance parameters of a multiplier.

1. Accuracy : It is the maximum deviation of the actual output level from the ideal one. This deviation is also called total error. It is generally specified interms of percentage of full scale output.

2. Linearity : It is the maximum output deviation from the best fit straight line at the output, where one input is varied from end to end while the other is kept fixed, usually at + 10 V or - 10 V. It is also expressed interms of percentage of full scale output.

3. Bandwidth : It is the range upto the frequency where the output is 3 dB below its low frequency value. This is also called as small signal bandwidth. It depends on the active device used.

4. 1 % absolute error bandwidth : It represents the frequency where the output magnitude starts to deviate from its low frequency value by one percent.

5. Feed through voltage : It is the peak to peak voltage at the output when one of the two inputs is grounded. As the output is the multiplication of the two inputs,

if one of the inputs is made zero, the output of ideal multiplier also must be zero. But in practice, there exists a small voltage at the output. This voltage is different for the two input terminals.

6. Zero trim : It is the ability of the multiplier to set the feed through voltage at the output to zero.

7. Scale factor : It is the proportionality constant (K) relating the output voltage and the product of the two input voltages.

K = V_o / V₁ V₂   ... (4.8.3)

8. Quadrant : This indicates the restriction on the polarities of the two input voltages. For one quadrant operation, both the inputs must be positive, for two quadrant one must be positive while the other can be bipolar. And for the four quadrant operation, both the inputs can be bipolar.

 

2. Applications of Multiplier

The multiplier is used in many practical applications. Some of these applications are:

1. In communication it is used in amplitude modulation, phase modulation, frequency modulation, phase detection, suppressed carrier modulation etc.

2. In instrumentation and control used to measure velocity, acceleration, instantaneous power, automatic gain control, etc.

3. For voltage controlled attenuators and for voltage controlled amplification.

4. It is used for voltage divider, true r.m.s calculation, rectifier phase shift detection etc.

5. It is used for frequency converters, frequency doubling and frequency shifting etc.

6. It is used for squaring and square root calculations.

7. It is used to solve nonlinear equations.

8. It is used in oscillators to generate the waveforms and also used for square wave generation etc.

Let us discuss, few of these applications in detail along with the circuit diagram and the operation.

a. Voltage Divider using Multiplier

The circuit in which output is the division of the two input signals, is called as a voltage divider. The use of multiplier as a voltage divider is shown in the Fig. 4.8.3. 

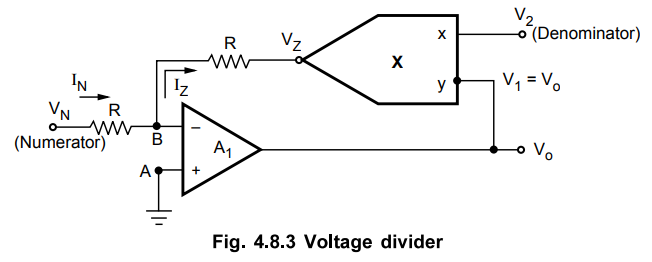
The multiplier is used in the feedback loop. The denominator is applied at the x input of the multiplier which is the voltage V₂. The numerator is applied at the input terminal of op-amp A₁.

As node A is grounded, node B is also at virtual ground, hence VB = 0. As op-amp input current is zero,

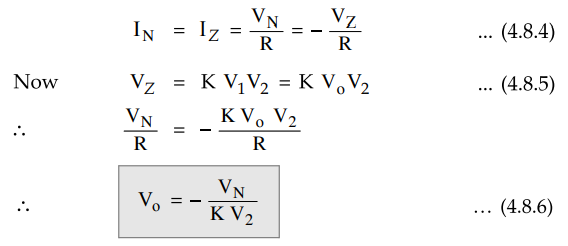
Thus the output is proportional to the division of the two input voltages V_N and V₂. The only requirement is that the input voltage V₂ must be negative. Hence divider circuits are at best two quadrant circuits.

b. Squaring Circuit using Multiplier

The squaring circuit gives square of the input voltage applied. The multiplier inputs are connected together to get the squaring circuit as shown in the Fig. 4.8.4.

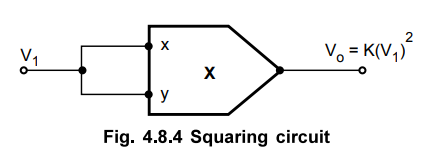
The same signal V₁ is applied to both the input terminals of the multiplier.

So V₂ = V₁   and hence the output of the multiplier is,

V_o = K V₁ V₂   = K (V₁)²  ….. (4.8.7)

Thus the output is proportional to the square of the input. 

c. Square Rooting Circuit using Multiplier

Similar to the squaring, the square rooting circuit can be obtained using multiplier. The circuit is shown in the Fig. 4.8.5.

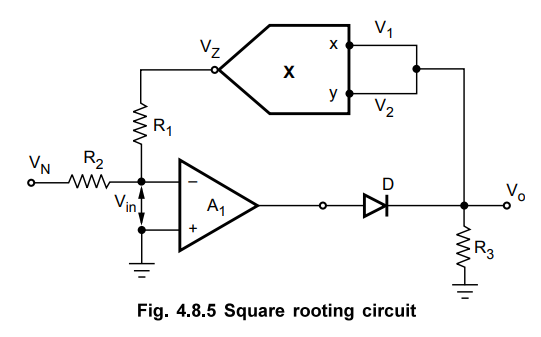
A multiplier configured as squaring circuit is used in the feedback loop. The gain of the op-amp A₁ is say A and voltage between inverting a nd non-inverting terminal is V_in. So we can write,

V_o = - V_in × A 

V_in = - V_o / A  ….. (4.8.8)

Now the voltage V_in is composed of two components, one that of V_Z and other that of V_N.

As seen from the equation (4.8.13), the output is proportional to the square root of V_N, but the V_N must be always negative, (V_N < 0). Otherwise the circuit becomes latched up and normal operation can only be restored by breaking the feedback loop. To avoid such problem, a series diode D is provided.

d. Frequency Doubler using Multiplier

The multiplication of two sine waves of same frequency but of possibly different amplitudes and phases, gives us a signal of a double frequency.

Consider the two input signals as,

V₁ = V_1m sin ω t and V₂ = V_2m sin (ω t + θ )

When the two inputs are given to a multiplier we get,

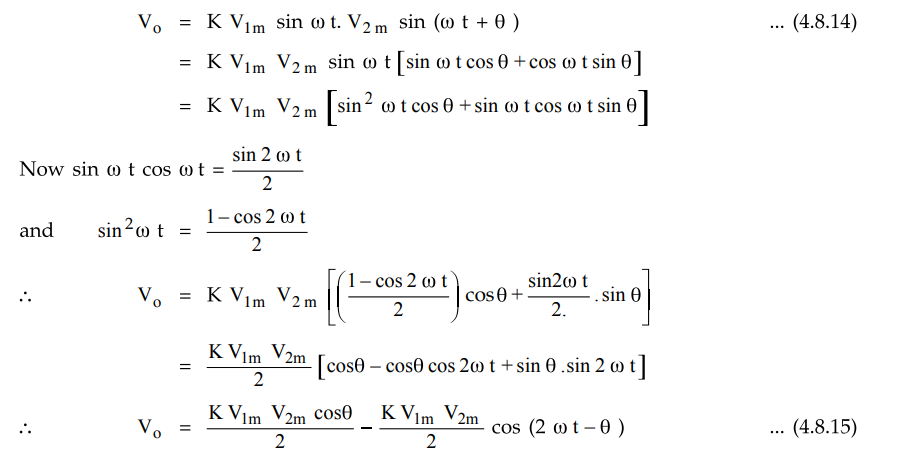
The first term is D.C. for a phase difference of θ while the second term varies with time but at twice the frequency of the inputs. Thus circuit acts as a frequency doubler.

Such a frequency doubler can be obtained by using a squaring circuit, as shown in the Fig. 4.8.6.

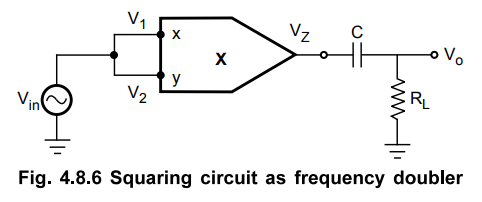
The two inputs are connected together hence

V₁ = V₂ = V_in = V_m sin ω t

Here θ = 0° which is phase difference between the two inputs.

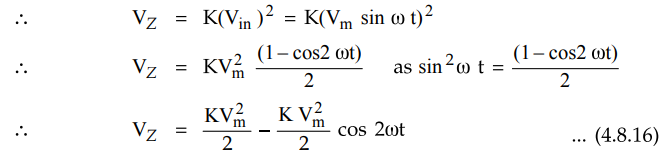
Thus the output of the multiplier is the D.C. signal with time varying signal of double the input frequency.

The capacitor C connected in series with the output blocks the D.C. and removes it. Thus we get,

Thus the circuit acts as a frequency doubler.

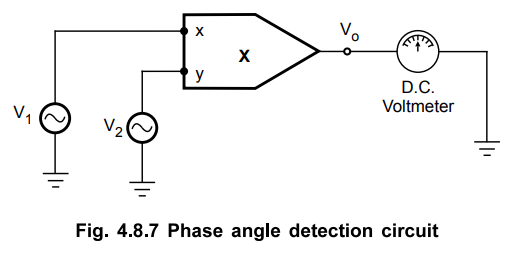
e. Phase Angle Detection using Multiplier

The frequency doubler circuit with two inputs of same frequency but different amplitudes and v phases can be used to obtain the phase angle detection circuit, as shown in the Fig. 4.8.7.

 As seen earlier, the output of the multiplier is

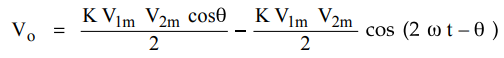
This is because, circuit acts as a frequency doubler. Now the D.C. voltmeter is connected at the output. The voltmeter will not respond to a.c. component present in the output, while the d.c. component can be easily measured on the voltmeter.

So calibrating the d.c. voltmeter as a phase angle meter, the phase angle between the two inputs can be measured.

f. RMS Detector

The RMS value of a signal is given by,

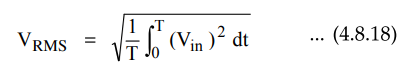
The operation is performed in reverse order as squaring, finding the mean i.e. integrating and finally finding the square root. The Fig. 4.8.8 shows the basic circuit for the RMS detector.

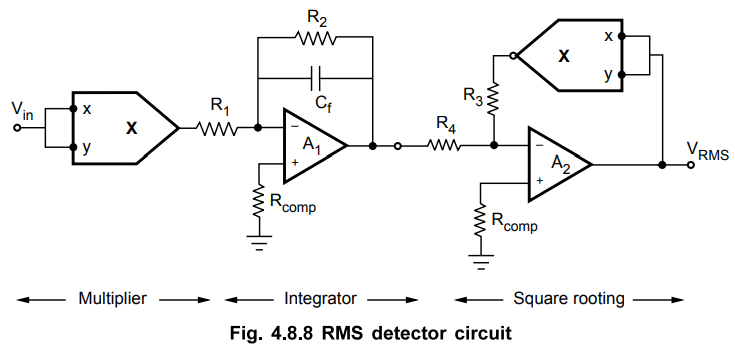
The circuit has a multiplier as a squaring device as its first element. This gives square of the input, the op-amp A1 is an integrator which gives the integration of squared input. Finally op-amp A2 along with the multiplier in its feedback loop performs square rooting operation, on the output of op-amp A1. Thus the final output is the RMS value of the input applied.

g. Rectifier using Multiplier

A full wave rectifier circuit using multiplier is shown in the Fig. 4.8.9.

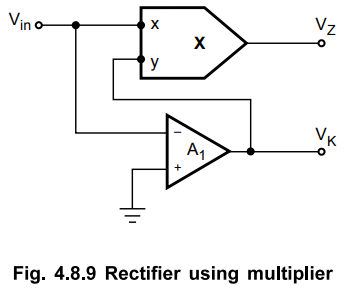
The op-amp A₁ is used as a non-inverting comparator. The output of op-amp A₁ is V_K and which is at ± V_sat depending upon whether the input V_in is positive or negative.

The multiplier used is a four quadrant multiplier whose output is always positive. Hence we get the full wave rectified signal at V_z while the square wave signal at V_K. The waveforms are shown in the Fig. 4.8.10.

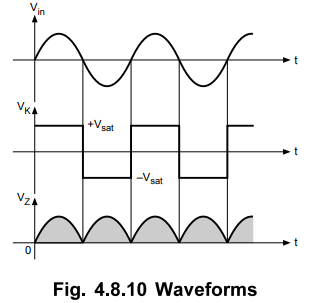
Key Point As the output of the multiplier is always positive, the circuit is also called as absolute value circuit.

 

3. Study of Multiplier ICs

a. Study of Multiplier ICs AD 533

The IC AD 533 is a multiplier IC by Analog Devices. It is a low cost integrated circuit comprising a transconductance multiplying element, stable reference and an output amplifier, on a monolithic silicon chip.

The various features of AD 533 are :

1) Its operation is very simple.

2) Only four external adjustments are necessary.

3) Maximum four quadrant error is below 0.5 %.

4) Its temperature drift is as low as 0.01 %/ °C

5) It is suitable for the applications like multipliers, dividers, square and square root extractor circuits etc, alongwith the operational amplifier.

The specified accuracy for the multiplifer can be easily achieved, by the straight forward adjustment of feedthrough, output zero and gain trim pots.

The scale factor of AD 533 is 1/10 for four quadrant operation hence it multiplies in four quadrants with a transfer function of XY/10. It divides in two quadrants with a transfer function of 10Z/X. While it calculates square root with a transfer function of -√10Z.

All models of AD 533 are available in hermetically sealed TO-100 and metal can packages or TO-116 ceramic DIP packages. The pin diagram of AD 533 is shown in the Fig. 4.6.11.

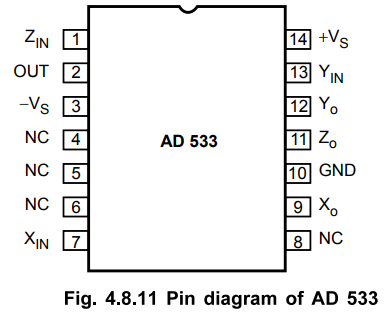
AD 533, for operation from -55 °C to +125 °C, has a maximum 1 % error in multiplying, at 25 °C. 

The op-amp output provides ± 10 V at 5 mA and is fully protected against short circuits to ground or either supply voltage. All the inputs are fully protected against over voltage transients.

The device has excellent a.c. performance with typical small signal bandwidth of 1 MHz and the slew rate of 45 V/µsec.

The low cost and simplicity of operation of the AD 533 make it especially well suited for use in the widespread applications such as,

1) Function generation

2) Peak detection

3) RMS compution

4) Automatic gain control

5) Frequency discrimination

6) Phase detection

7) Square and square root extractor

8) Modulation and demodulation

Use of AD 533 is some of the basic applications is discussed here.

1. AD 533 as Multiplier

The connection diagram of AD 533 as a multiplier, alongwith the component values is shown in the Fig. 4.8.12. 

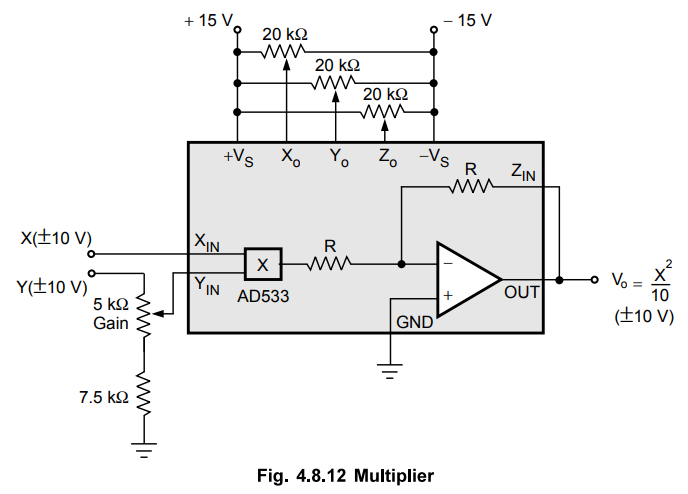
The multiplier operation is possible by closing the loop around the internal op-amp with the Z input connected to the output.

The Xo null pot balances the X input channel to minimize Y feedthrough and the Yo null pot balances the Y input to minimize X feedthrough. The Z_o pot compensates the output op-amp offset voltage. The gain pot sets the full scale output level.

The output is given by,

V_o =XY / 10

2. AD 533 as Squarer

The connection diagram of AD 533 as a squarer alongwith the component values is shown in the Fig. 4.8.13.

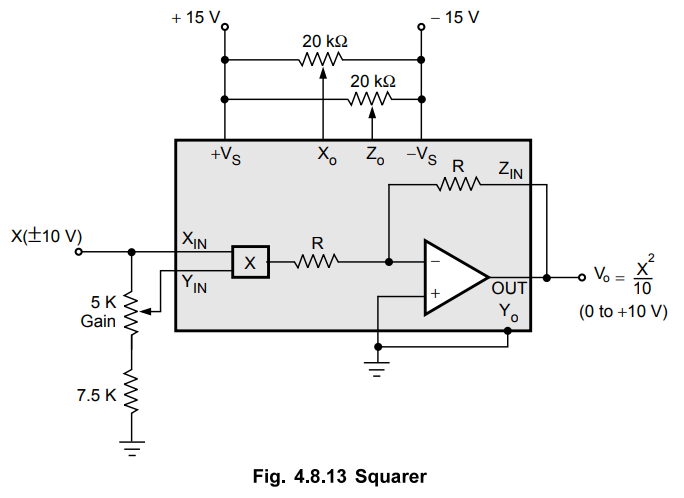
The squarer is a special case of multiplier operation where both the input X and Y are connected together and two quadrant operation results. The output is always positive. When the X and Y inputs are connected together then combined offset which is algebraic sum of the individual offsets, results. This can be nulled using the X_o pot alone. The output is given as,

V_o = XY / 10 = X² / 10

3. AD 533 as Divider

The connection diagram of AD 533 as divider is shown in the Fig. 4.8.14.

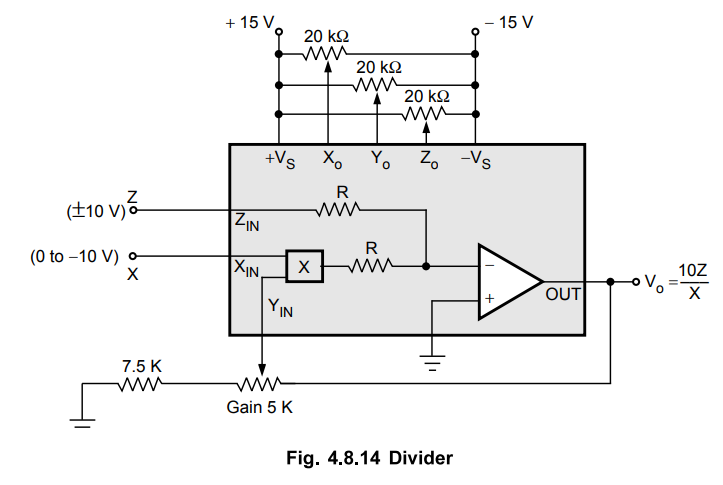
The divide mode utilises the multiplier in a fedback configuration where the Y input now controls the feedback factor. With X = full scale, the gain V_o /Z becomes unity after trimming. Reducing the X input, reduces the feedback around the op-amp by a like amount, thereby increasing the gain. This reciprocal relationship forms the basis of the divide mode.

The output is given by,

V_o = 10Z / X

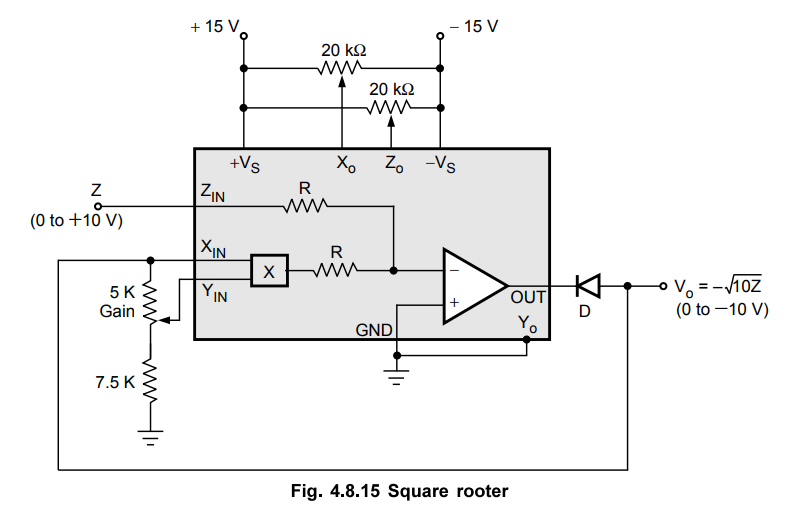
4. AD 533 as Square Rooter :

The connection diagram of AD 533 as a square rooter is shown in the Fig. 4.8.15, alongwith the component values. This mode is also a feedback configuration. Both X and Y inputs are tied to the op-amp output through an external diode to prevent latchup.

Accuracy, noise and the frequency response are proportional to the √Z, which implies a wider usable dynamic range than the divide mode.

The output is given as, 

Vo = -√10Z

b. Study of Multiplier IC : AD 534

The IC AD 534 is a multiplier IC by Analog Devices. It is a monolithic laser trimmed four quadrant multiplier, having a maximum multiplication error of ± 0.25 %. It does not require any external trimming. It has excellent supply rejection, low temperature coefficient and long term stability. It preserves the accuracy even under adverse conditions of use.

It is the first multiplier to offer fully the differential, high impedance operation on all inputs, including the Z input. This has increased its flexibility and simplicity of use.

The scale factor is pretrimmed to the standard value of 10.00. By means of the external resistor, the scale factor can be reduced to the values as low as 3, with corresponding reductions in bias current and noise level. Its operating temperature range is -55°C to+ 125°C.

The AD 534 is the first general purpose multiplier, capable of providing gains upto X100. It does not require the separate instrumentation amplifiers for preconditioning of the inputs. The AD 534 can be very effectively employed as a variable gain differential input amplifier with high Common Mode Rejection Ratio (CMRR). The gain option is available in all the modes. It is very simple to implement many function fitting algorithms as used to generate sine and tangent, with AD 534. The utility of this feature is enhanced by the inherent low noise of the AD 534 which is 90 |iV rms (depending on the gain). Drift and feedthrough are also substantially reduced over earlier designs. The precise calibration and differential Z input makes the AD 534 more flexible compared to  other multipliers. The standard MDSSR (Multiplication, Division, Square and Square rooting) functions can be very easily implemented using AD 534. The output can be in the form of a current if required, facilitating the operations such as integration.

The various features of AD 534 are

1) Pretrimmed to ± 0.25 % maximum four quadrant error.

2) All the inputs X,Y and Z are differential.

3) The adjustable scale factor.

4) Low noise design : 90 µV rms for 10 Hz -10 kHz

5) Low cost monolithic construction

6) Excellent long term stability

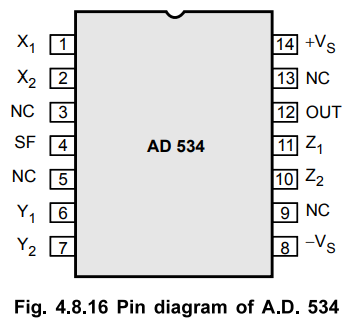
All the grades of AD 534 are available in hermetically sealed TO-100 metal cans and TO-116 ceramic DIP packages. The pin diagram of AD 534 is shown in the Fig. 4.8.16.

The low cost and simplicity of operation of the AD 534 make it suitable for use in the applications such as,

1) Multiplier

2) Divider

3) Squarer and square rooter

4) High quality analog signal processing

5) Differential ratio and percentage computations

6) Algebraic and Trignometric function synthesis

7) Wideband and high crest rms to dc conversion

8) Accurate voltage controlled oscillators and filters

Use of AD 534 in some of the basic applications is discussed here.

1. AD 534 as Divider

The AD 534 as divider is shown in the Fig. 4.8.17.

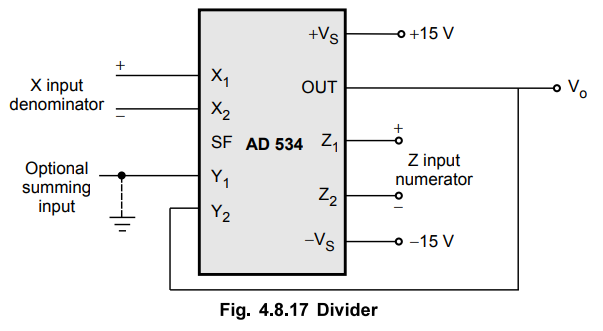
AD 534 provides the differential operation on both numerator and denominator. This allows the ratio of two floating variables to be generated. Further flexibility is possible from access to a high impedance summing input to Y₁. The bandwidth is proportional to the denominator magnitude.

Without additional trimming, the accuracy of AD 534 is sufficient to maintain a 1% error over 10 V to 1 V denominator range.

The overall gain can be introduced by inserting a simple attenuator between the output and Y₂ terminal.

This option and the differential ratio capability of AD 534 is utilised in the percentage computer applications.

The output of the AD 534 as a divider circuit, is

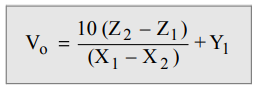
2. AD 534 as Square Rooter

The square rooter circuit connections using AD 534 is shown in the Fig. 4.8.18.

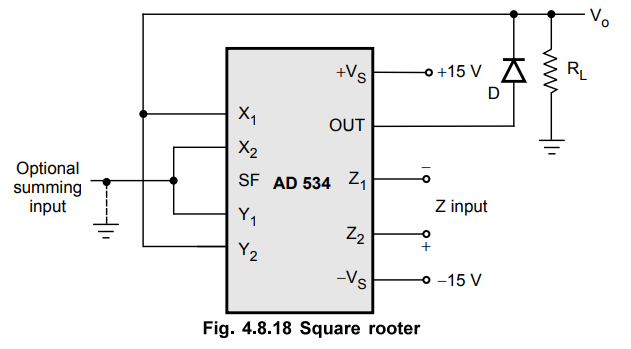
The diode D prevents a latching condition which could occur if the input momentarily changes the polarity. The output is always positive.

The output can be changed to negative by reversing the diode direction and interchanging the X inputs.

Since the signal input is differential, all the combinations of input and output polarities can be realized but operation is restricted to the one quadrant associated with each combination of inputs. 

The output of the circuit is given as,

Vo = √10(Z₂ – Z₁) + X₂

Review Questions

1. Draw the symbol of analog multiplier IC and write expression for output voltage. List its applications and explain any two.

May-07, Marks 8

2. With circuit schematic explain how the multiplier IC AD533 can be used as squarer and divider circuits.

Dec.-09, Marks 8

3. Write a note on analog multipliers.

Dec.-08, 17, Marks 10

4. Explain how to measure the phase difference between two signals.

Dec.-15, Marks 4