Analysis of CE Amplifier with Collector to Base Bias

Analysis of CE Amplifier with Collector to Base Bias

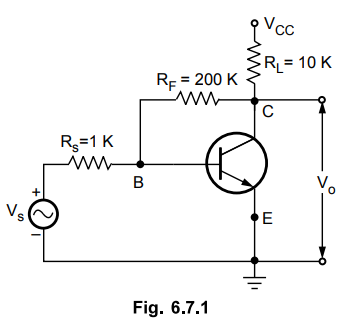
• The Fig. 6.7.1 shows the common emitter amplifier with collector to base bias.

• As shown in the Fig. 6.7.1, the resistance RF in this configuration is connected between input and output.

• For the analysis of this circuit it is necessary to split this resistance for input and output. This can be achived by using Miller’s theorem.

1. Miller’s Theorem

• In general, the Miller theorem is used for converting any circuit having configuration of Fig. 6.7.2 (a) to another configuration shown in Fig. 6.7.2 (b).

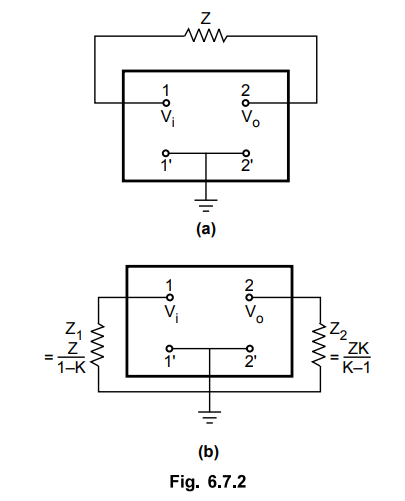
• The Fig. 6.7.2 shows that, if Z is the impedance connected between two nodes, node 1 and node 2, it can be replaced by two separate impedances Z₁ and Z₂; where Z₁ is connected between node 1 and ground and Z2 is connected between node 2 and ground.

• The Vi and Vo are the voltages at the node 1 and node 2 respectively. The values of Z1 andZ2 can be derived from the ratio of Vo and V; (Vo / Vi), denoted as K. Thus it is not necessary to know the values of V; and Vo to calculate the values of Zi and Z2.

• The values of impedances Z₁ and Z₂ are given as Z

Z₁  = Z / 1 – K … (6.7.1)

And Z₂  = Z.K / K – 1 … (6.7.2)

2. Proof of Miller's Theorem

Miller's theorem states that, the effect of resistance Z on the input circuit is a ratio of input voltage V to the current I which flows from the input to the output.

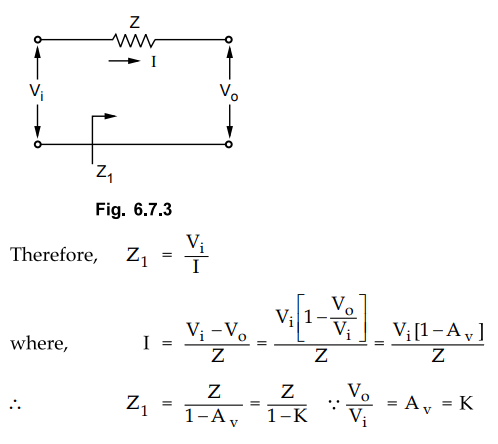
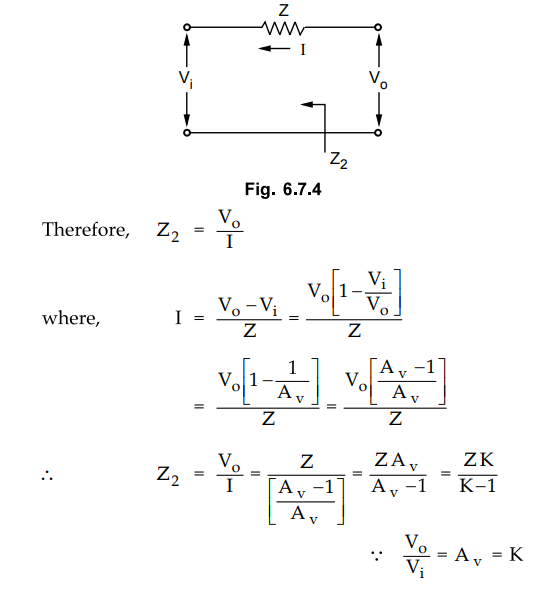
• Miller's theorem states that, the effect of resistance Z on the output circuit is a ratio of output voltage Vo to the current I which flows from the output to the input.

3. Analysis using Miller's Theorem

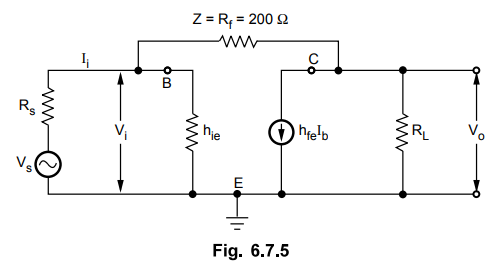
• For the common emitter amplifier with collector to base bias shown in Fig. 6.7.5, calculate R_i, A_i , A_v A_vs and Ro. The transistor parameters are hie = 1.1 K, h_fe = 50, h_oe = h_re = 0 . Assume R_L = 10 K and R_s = 1 K

H-parameter equivalent circuit :

• The Fig. 6.7.5 shows the approximate h-parameter equivalent circuit for the amplifier shown in Fig. 6.7.1.

• Applying Miller's theorem we get simplified circuit as shown in the Fig. 6.7.6. The voltage Av of the circuit can be given as Vo / Vi. AS the amplifier is a common emitter amplifier we can assume that the voltage gain Av >> f i.e. K >> 1. This assumption makes it easier to calculate the value of Z₂. Z₂ is given as,

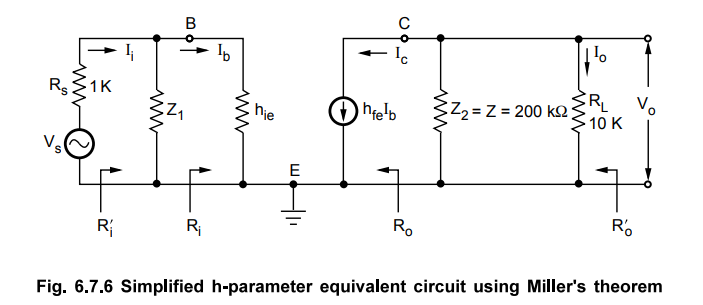
Z₂ = Z • K / K – 1 = Z • K / K    K >> 1

Z₂ = Z = 200 kΩ

However, we do not know the exact value of Av, thus we cannot calculate exact value of Z1 at this stage.

Analysis :

Since h _oe = h _re = 0, we use approximate analysis

a) Current gain ( A_i ) = - h_fe = - 0

b) Input resistance ( R_i ) = h_ie = 1.1 kΩ

c) Voltage gain (A_v) = A_i R_L / R_i

Ex. 6.7.1 The transistor used in the circuit of Fig. 6.7.9 has following parameters, h_fe = 500 Ω,

h_re = 2.4 × 10^{- 4}, h_fe = 60 and h_oe = 1/40 K. Calculate R_v, R_i  , A_I , A_V , A_Ve = A_Ve = V_o / V_s , A_I = I_L / I_s  and R'_o. Assume all capacitors to be very large.

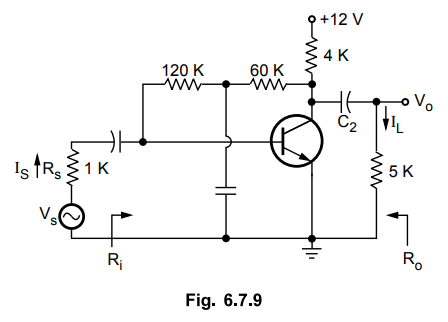
Sol. : For the given circuit h_oe × R'_L where

R'_L=(R_L ||R) = 1 / 40 × 10³ × (60K||4K|| 5K) = 0.0536,

which is less than 0.1. Thus we analyze given circuit with approximate method. Fig. 6.7.10 shows approximate h-parameter equivalent circuit for given circuit. It is drawn by replacing all capacitors and d.c. source with short circuits and replacing transistor with its h-parameter equivalent circuit. 

Review Question

1. Define Miller's theorem.