Electric Circuit Analysis: Unit V: Resonance and coupled circuits
Analysis of coupled circuits
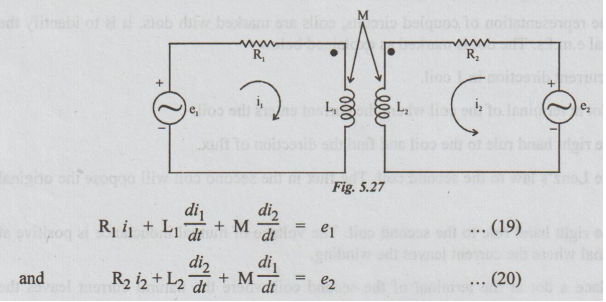
Each circuit contains a voltage source. As both currents i, and i2 enter the coils through the dotted ends, M is taken as positive. By applying KVL, the two loop equations may be written as below
ANALYSIS OF COUPLED CIRCUITS
Consider
the coupled circuits.
Each
circuit contains a voltage source. As both currents i, and i2 enter the coils
through the dotted ends, M is taken as positive. By applying KVL, the two loop
equations may be written as below:
In
the sinusoidal steady state the above equations become,
(R1
+ jωL1) I1 + jωMI2 = E1 …
(21)
joM
I1 + (R2 + jωL2) = E2 … (22)
In
the matrix form, the last two equations may be written as,
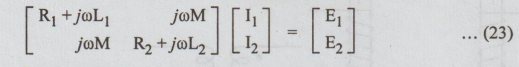
The
equations (21) & (22) may be written as
[R1
+ jω (L1 – M + M) I1 ] E1 … (24)
and
jωMI1 + (R2 – jω (L2 – M + M) ] I2
… (25)
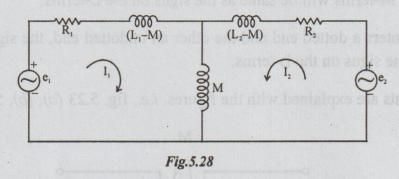
The
coupled circuit of fig. 5.20 may be now re-drawn as in fig. 5.28. It is called
conductively coupled equivalent circuit of the mutually coupled circuit. It is
so called because of the common conducting element M.
Electric Circuit Analysis: Unit V: Resonance and coupled circuits : Tag: : - Analysis of coupled circuits
Electric Circuit Analysis: Unit V: Resonance and coupled circuits
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation