Analysis of Feedback Amplifiers

Analysis of Feedback Amplifiers

AU : May-06, 07, 10, 11, 12, 13, 15, 16, Dec.-05, 08, 10, 14, 15

 

1. Voltage Series Feedback

• Fig. 9.12.1 shows the transistor emitter follows circuit. Here, feedback voltage is the voltage across Ro and sampled signal is Vo across Re.

Analysis

Step 1 : Identify topology

• By shorting output voltage (Vo = 0), feedback signal becomes zero and hence it is voltage sampling. Looking at Fig. 9.12.1 we can see that feedback signal Vf is subtracted from the externally applied signal Vs and hence it is a series mixing. Combining two conclusions we can say that it is a voltage series feedback amplifier.

Step 2 and Step 3 : Find input and output circuit

• To find the input circuit, set Vo = 0, and hence Vs in series with Rs appears between B and E. To find the output circuit, set Ii = Ib = 0, and hence Re appears only in the output loop. With these connections we obtain the circuit as shown in the Fig. 9.12.2

Step 4 : Replace transistor by its h-parameter equivalent circuit

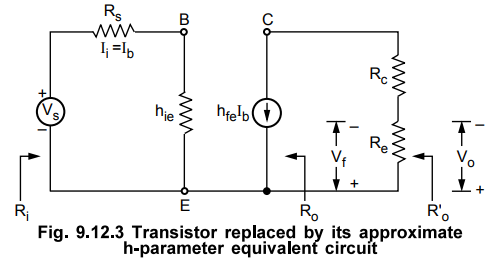
Step 5 : Find open loop voltage gain

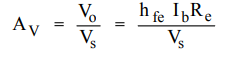
Applying KVL to input loop we get

V_s = I_b (R_s + h_ie)

Substituting value of V_s we get

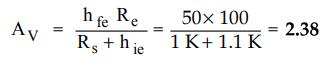
Step 6 : Indicate Vo and Vf and calculate β

• The output resistance is measured by making

Vs = 0. Since Vs = 0, Ib = 0 and hence hfeIb = 0, as shown in the Fig. 9.12.4.

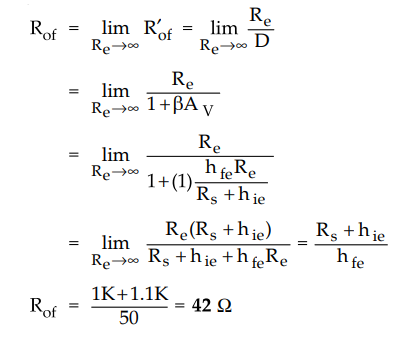
• The indeterminancy R_of = ∞ may resolved by deriving R_of interms of R_of.

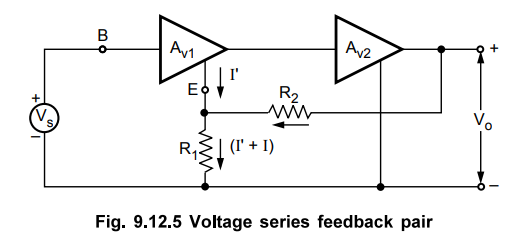
a. Voltage Series Feedback Pair

• Fig. 9.12.5 shows two cascaded stages. The output of second stage is connected through feedback network to the input of first stage in opposition to the input signal Vs.

Analysis :

Step 1 : Identify topology

• By shorting output voltage V_o = 0, feedback signal becomes zero and hence it is voltage sampling. Looking at Fig. 9.12.5 we can see that feedback signal Vf is subtracted from the externally applied signal Vs and hence it is a series mixing. Combining two conclusions we can say that it is a voltage series feedback amplifier.

Step 2 and Step 3 : Find input and output circuit

• To find input circuit, set Vo = 0 in Fig. 9.12.5 and hence R2 appears m parallel with Rj at first emitter. To find the output circuit, set Ii = 0 in Fig. 9.12.5 and hence T = 0 (open circuit) and Rj appears in series with R2 across output. The resulting circuit is shown in Fig. 9.12.6.

For this circuit, feedback factor β can be calculated as

β = V_f / V_o = R₁ / R₁ + R₂

 

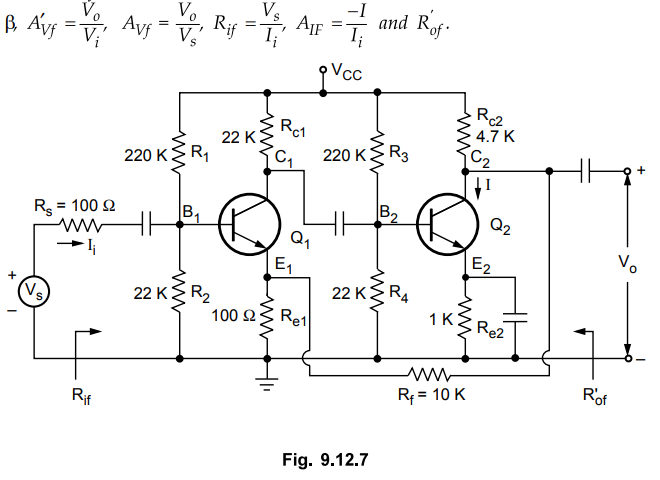
Ex. 9.12.1 Transistors in the feedback amplifier shown in Fig. 9.12.7 are identical and their 'h' parameters are hie =1100 Ω hf= 50, hre = hoe= 0. Neglect capacitances of all capacitors.

i) State topology with justification, ii) Calculate

Sol : Step 1 : Identify topology

The feedback voltage is applied across the resistance Re1 and it is in series with input signal. Hence feedback is voltage series feedback.

Step 2 and Step 3 : Find input and output circuit

To find input circuit, set Vo = 0 (connecting C2 to ground), which gives parallel combination of Re with Rf at Ep To find output circuit, set Ii = 0 (opening the input node E1 at emitter of Q1), which gives series combination of Rf and Re1 across the output. The resultant circuit is shown in Fig. 9.12.8.

Step 4 : Replace transistors with hybrid equivalent circuit.

 

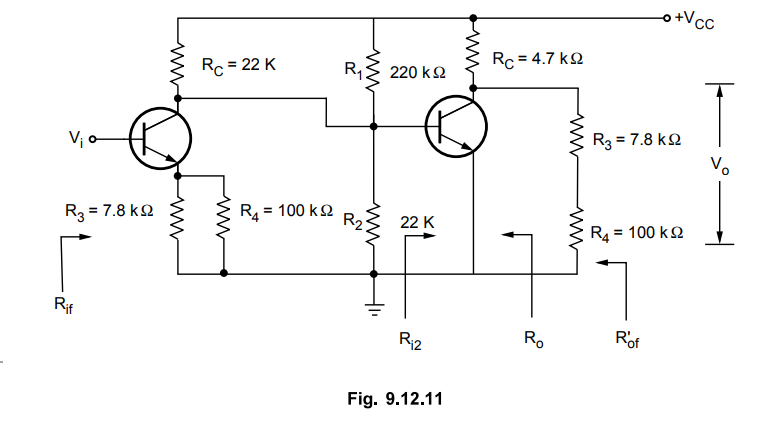
Ex. 9.12.2 Find the voltage gain, feedback factor, input resistance and output resistance of a series-shunt pair type two stage feedback amplifier using transistors with hfe = 99 and hig = 2 k Ω, shown in Fig. 9.12.10.

Sol. : Step 1 : Identify topology

The feedback voltage is applied across the resistance R4 and it is in series with input signal. Hence feedback is voltage series feedback.

Step 2 and Step 3 : Find input and output circuit. To find input circuit, set V = 0, which gives parallel combination of R4 with R3 at Ej. To find output circuit, set Ij = 0, which gives series combination of R3 and R4 across the output. The resultant circuit is shown in the Fig. 9.12.11.

Step 4 : Find open loop voltage gain (A_V)

 

Ex. 9.12.3 For feedback amplifier shown in Fig. 9.12.13, identify the feedback topology with proper justification. The transistors used are identical with the following parameters :

Sol. : Step 1 : Identify topology.

The feedback voltage is applied across Rgl = 1.5 K, which is in series with input signal. Hence feedback is voltage series feedback.

Step 2 and Step 3 : Find input and output circuit To find input circuit, set VQ = 0, which gives parallel combination of Rgl with Rf at Ej as shown in the Fig. 9.12.14. To find output circuit, set L = 0 by opening the input node, Ej at emitter of Qj, which gives the series combination of Rf and Rgl across the output. The resultant circuit is shown in Fig. 9.12.14.

Step 4 : Find the open loop voltage gain (A_V).

Example for Practice

Ex. 9.12.4 Transistors in the feedback amplifier shown in Fig. 9.12.16 are identical and transistor parameters are hle = 1.1 K, h^, = 50, hre =   = 0. Identify the feedback amplifier and calculate Avf, R'of and Rlf.

AU : ECE : Dec.-lO, Marks 16

[Ans.: Voltage series feedback amplifier, A_vf = 45.46, Ro =112 k Ω, Rif = 27.12 kQ, R_of = 129 Ω]

 

2. Current Series Feedback

• Fig. 9.12.17 shows the common emitter circuit with imbypassed Rg. The common emitter circuit with unbypassed Rg is an example of current series feedback. In this configuration resistor Re is common to base to emitter input circuit as well as collector to emitter output circuit and input current Ib as well as output current Ic both flow through it. The voltage drop across R_E

• V_f = (I_b + I_c) Re = Ie Re ≈ R Re = Io R Re’ This voltage droP shows that the output current I is being sampled and it is converted to voltage by feedback network. At input side voltage Vf is subtracted from Vg to produce V.. Therefore, the feedback applied in series.

Analysis

Step 1 : Identify topology

• By opening the output loop, (output current, Io = 0), feedback signal becomes zero and hence it is current sampling. Looking at Fig. 9.12.17 we can see that feedback signal Vf is subtracted from the externally applied signal V hence it is a series mixing. Combining two conclusions we can say that it is a current series feedback amplifier.

Step 2 and Step 3 : Find input and output circuit

• To find input circuit set Io = 0, then R appears at the input side. To find output circuit set I; = 0, then Re appears in the output circuit. The resulting circuit is shown in the Fig. 9.12.18.

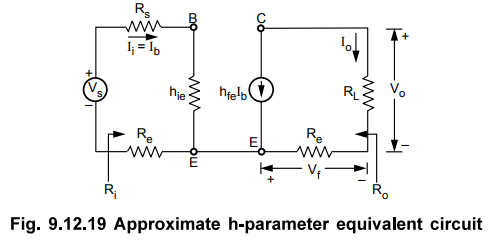
Step 4 : Replace transistor with its approximate h-parameter equivalent circuit

• Fig. 9.12.19 shows the approximate h-parameter equivalent circuit

 Step 5 : Find open loop transfer gain

 

Ex. 9.12.5 For the circuit shown in Fig. 9.12.20. i) Identify topology used in feedback amplifier ii) Show that voltage gain with feedback

Sol. :

Step 1 : Identify topology

By shorting output (V = 0), feedback voltage does not become zero. By opening the output loop feedback becomes zero and hence it is current sampling. The feedback is applied in series with the input signal, hence topology used is current series feedback.

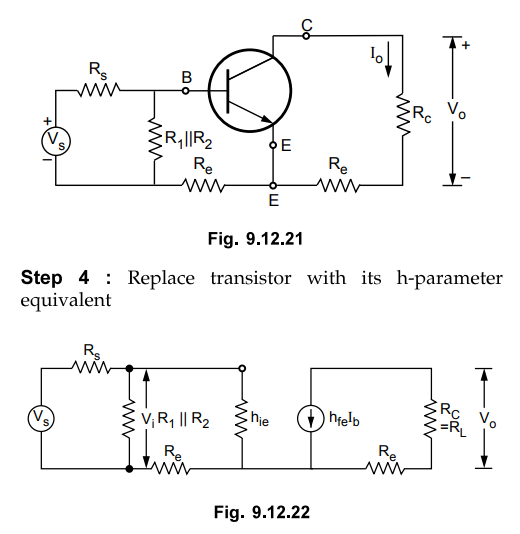
Step 2 and Step 3 : Find input and output circuit To find input circuit, set I = 0. This places Rg in series with input. To find output circuit L = 0. This places Rg in the output side. The resultant circuit is shown in Fig. 9.12.21.

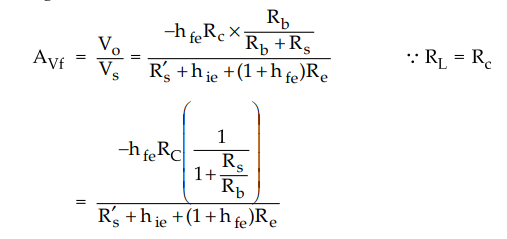
Step 5 : Find open loop transfer gain

Referring expressions of GM, D and P from previous example we have,

Dividing both numerator and denominator by Rs + Rb

we get

 

Ex. 9.12.6 A current series feedback amplifier is shown in the Fig. 9.12.23 below.

It has the following parameters :

Sol. : The Fig. 9.12.24 shows the equivalent circuit for the given current series feedback amplifier.

 

3. Current Shunt Feedback

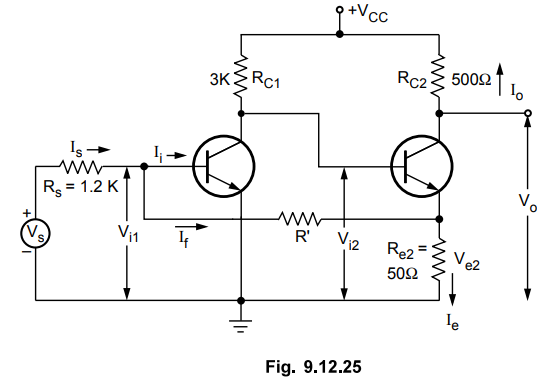
• Fig. 9.12.25 shows two transistors in cascade connection with feedback from second emitter to first base through resistor R'. Here, the feedback network formed by R' and Re2 divides the current Ig. Since I = - 1^ the feedback network gives current feedback. At input side, we see that I; = Is - If, i.e. If is shunt subtracted from Ig to get If Therefore, this configuration is a current shunt feedback.

Step 1 : Identify topology

• By shorting output voltage (V = 0), feedback signal does not become zero and hence it is not voltage sampling. By opening the output loop (Io = 0), feedback signal becomes zero and hence it is a current feedback. The feedback signal appears in shunt with input (Ii = Is -If ) hence the topology is current shunt feedback amplifier.

Step 2 and Step 3 : Find input and output circuit

• The input circuit of the amplifier without feedback is obtained by opening the output loop at the emitter of Q2 (Io = 0). This places R' in series with Rg from base to emitter of Qr The output circuit is found by shorting the input node (the base of Qf), i.e. making V. = 0. This places R' in parallel with Rg. The resultant equivalent circuit is shown in Fig. 9.12.26.

Step 4 : Find open circuit transfer gain

Substituting the numerical values obtained from equations (9.12.11), (9.12.12), (9.12.13) and (9.12.14) in equation (9.12.10) we get,

From calculation for A_I we note that A_I is independent of the load R_L = R_c2.

 

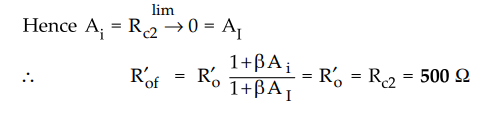
Ex. 9.12.7 In the two-stage feedback amplifier shown, the transistors are identical and have the following parameters

Sol. :

Step 1 : Identify topology.

Making output voltage zero (V = 0); feedback does not become zero and hence it is not voltage sampling. By opening the output loop feedback becomes zero and hence it is a current sampling. As I' = Ig - If, the feedback current appears in shunt with the input signal and hence the topology is current shunt feedback.

Step 2 and Step 3 : Find input and output circuit. To find input circuit, set I = 0. This gives series combination of resistors 10 K and 15 K across the input of the transistor Qr To find the output circuit, set Vj = 0. This gives parallel combination of resistors 10 K and 15 K at the emitter of the transistor Q2. The resultant circuit is as shown in the Fig. 9.12.28.

 

Ex. 9.12.8 The transistors in the feedback amplifier shown are identical and their h-parameters are hig = 1100 Q, bp = 50, hge = hrg = 0. Neglect the reactances of the capacitors. Calculate

Sol. :

Step 1 : Identify topology

Making output voltage zero(VQ = 0); feedback does not become zero and hence it is not voltage sampling. By opening the output loop feedback becomes zero and hence it is current sampling. As feedback current appears in shunt with the input signal, the topology is current shunt feedback.

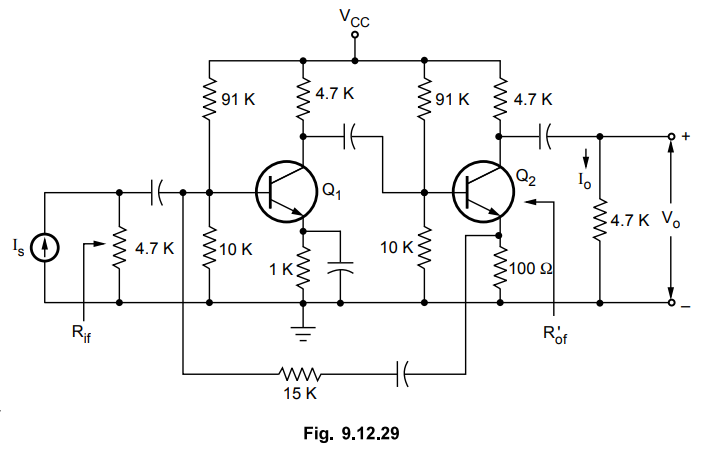
Step 2 and Step 3 : Find input and output circuit. To find input circuit, set I = 0. This gives series combination of resistors 15 K and 100 Ω across the input of the first transistor. To find output circuit, set V_i = 0. This gives parallel combination of resistors 15 K and 100 Ω at emitter of the second transistor. The Fig. 9.12.30 shows the resultant circuit with transistor is replaced by its h-parameter equivalent circuit.

Step 4 : Find open circuit current gain

 

Ex. 9.12.9 For the circuit shown in Fig. 9.12.31. Find

Sol. :

Step 1 : Identify topology

By opening the output current loop, feedback becomes zero, hence it is current sampling and feedback current appears in shunt with the input signal, hence it is a current shunt feedback.

Step 2 and Step 3 : Find input and output circuit. To find input circuit, set I = 0. This gives series combination of resistors 27 K and 3 K across the input of the transistors Qr To find the output circuit, set V. = 0. This gives parallel combination of resistors 27 K and 3 K at the emitter of the transistor Q2- The resultant circuit with transistor replaced by its h-parameter equivalent circuit is as shown in the Fig. 9.12.32.

 

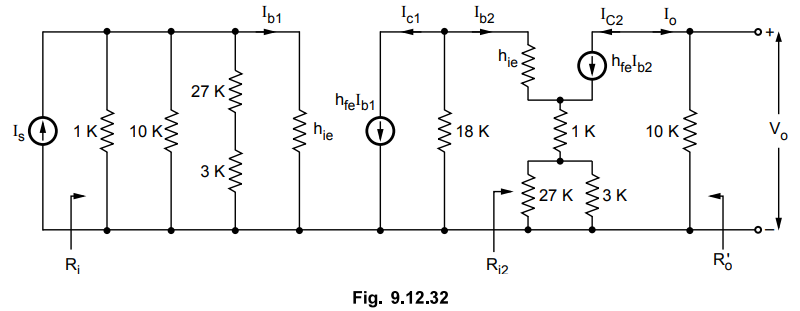
Ex. 9.12.10 For the transistor circuit shown in Fig. 9.12.34 :

i) Identify the topology of feedback

ii) Draw equivalent circuit diagram

iii) Calculate the values of A_I  β and A_If. Given for Q₁ and Q₂ h_fe = 50, h_ie = 1.1 kΩ.

Sol. : Step 1 : Identify topology

The feedback is given from emitter of Q2 to the base of Q2. If I = 0 then feedback current through R'(5 K) register is zero, hence it is current sampling. As feedback signal is mixed in shunt with input, the amplifier is current shunt feedback amplifier.

Step 2 and Step 3 : Find input and output circuit. The input circuit of the amplifier without feedback is obtained by opening the output loop at the emitter of Q2 (IQ = 0). This places R' (5 K) in series with Rg from base to emitter of Qr The output circuit is found by shorting the input node, i.e. making Vi = 0. This places R' (5 K) in parallel with Rg. The resultant equivalent circuit is shown in Fig. 9.12.34 (a).

 

4. Voltage Shunt Feedback

• Fig. 9.12.35 shows a common emitter amplifier with a resistor R' connected from the output to the input.

Step 1 : Identify topology

By shorting output voltage (V =0), feedback reduces to zero and hence it is a voltage sampling. As P = Js - Jf, the mixing is shunt type and topology is voltage shunt feedback amplifier.

Step 2 and Step 3 : Find input and output circuit. To find input circuit, set V = 0, this places R' between base and ground. To find output circuit, set V = 0, this places R' between collector and ground. Since it is a shunt feedback we use Norton's equivalent of the source, i.e. current source.

The resultant circuit is shown in Fig. 9.12.36.

• The feedback signal is the current If in the resistor R' which is in the output circuit as shown in the Fig. 9.12.36.

Step 4 : Replace transistor with its h-parameter equivalent circuit.

Substituting values of equation (9.12.16) and (9.12.17) in equation (9.12.15) we have

Simple way to calculate R'_of

 

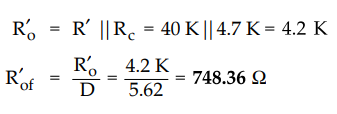
Ex. 9.12.11 For the transistor feedback amplifier shown,

Sol. :

Step 1 : Identify topology

By shorting output voltage (V =0), feedback reduces to zero and hence it is a voltage sampling. As -i = Is - If, the mixing is shunt type and topology is voltage shunt feedback amplifier.

Step 2 and Step 3 : Find input and output circuit. To find input circuit, set V = 0, this places R' between base and ground. To find output circuit, set V = 0, this places R' between collector and ground. Since it is a shunt feedback we use Norton's equivalent of the source, i.e. current source.

• The resultant circuit with transistor replaced by h-parameter equivalent is as shown in the Fig. 9.12.39.

Step 4 : Find the open circuit transresistance

 

Ex. 9.12.12 For the transistor amplifier stage shown in Fig. 9.12.40, hfe = 50, h_ie = 1.1 K, h_re = h_oe = 0. Analyse the circuit for : i) Type of feedback ii) β iii) RM iv) R_MF V) A_Vf   vi) R_iF vii) R_oF.

Sol. : Step 1 : Identify topology

By shorting output voltage (Vo = 0), feedback reduces to zero and hence it is a voltage sampling. As Ii = Is -If, the mixing is shunt type and hence topology is voltage shunt feedback amplifier.

Step 2 : Find the h-parameter equivalent circuit

Step 3 : Calculate β

Examples for Practice

Ex. 9.12.13 For the transistor feedback amplifier shown, h

 

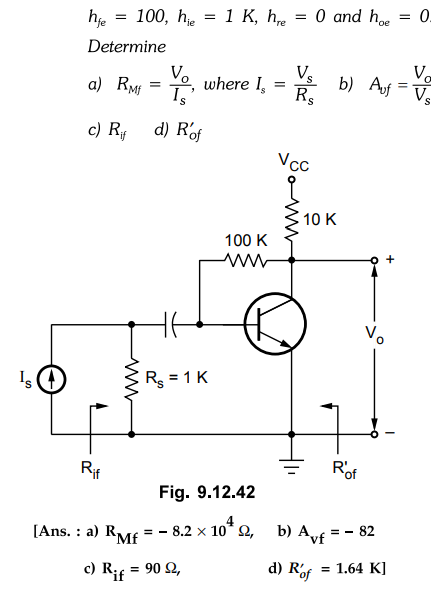
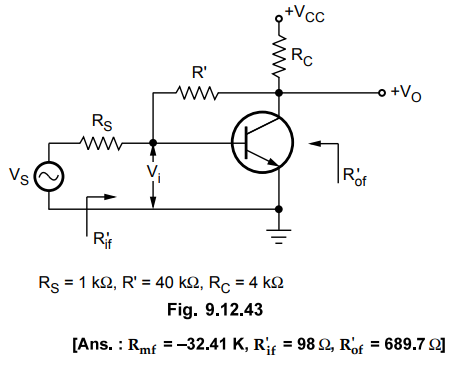
Ex. 9.12.14 For the transistor feedback stage shown in

Fig. 9.12.43 assume h_fe = 100, h_e = 1.1 K,h_oe = h_oe = 0.

1) Identify the topology with justification.

2) Calculate R_mf, R_if, R_of.

Review Questions

1. Draw example circuit for each type of feedback.

AU : ECE : May-06, Marks 6

2. Explain the current series feedback amplifier with a neat diagram.

3. Draw the circuit for voltage series feedback pair and derive expressions for R_if R_of and A_if.

4. Draw the circuit for common emitter configuration with unbypassed Rg and derive the expressions for R_if R_of and A_if.

AU : ECE : Hay-13, Marks 16

5. Draw the circuit for current shunt feedback and derive the expression for R_if R_of , A_vf  and A_if

6. Draw the basic circuit of the voltage shunt feedback amplifier and describe the concepts involved in such an amplifier.

AU : ECE : Dec.-05, Marks 8

7. Determine Ry^^A,, and A^ for the following : i) Voltage shunt feedback amplifier ii) Current series feedback amplifier.

AU : Dec.-14, Marks 16

8. Draw circuit of CE amplifier with current series feedback and obtain the expression for feedback ratio, voltage gain, input and output resistances.

AU : May-15, Marks 16

9. Sketch the circuit diagram of a two-stage capacitor coupled BJT amplifier that uses series voltage negative feedback. Briefly explain how the feed back operates.

AU : Dec.-15, Marks 16