Analytic functions

UNIT-III

ANALYTIC FUNCTIONS

Analytic functions - Necessary and sufficient conditions for analyticity in Cartesian and polar co-ordinates - Properties - Harmonic conjugates - Construction of analytic function - Conformal mapping - Mapping by functions w z + c, cz, 1/z, z2 - Bilinear transformation.

INTRODUCTION

The theory of functions of a complex variable is the most important in solving a large number of Engineering and Science problems. Many complicated integrals of real functions are solved with the help of a complex variable.

(a) Complex variable :

x + iy is a complex variable and it is denoted by z.

i.e., z = x + iy where i = √-1

(b) Function of a complex variable

If z = x + iy and w = u + iv are two complex variables, and if for each value of z in a given region R of the complex plane there corresponds one or more values of w, then w is said to be a function of z and is denoted by w = f(z) = f(x + iy) u (x, y) + iv (x, y) where u (x, y) and v (x, y) are real functions of the real variables x and y.

Note (i) Single-valued function :

If for each value of z in R there is correspondingly only one value of w, then w is called a single valued function of z. 

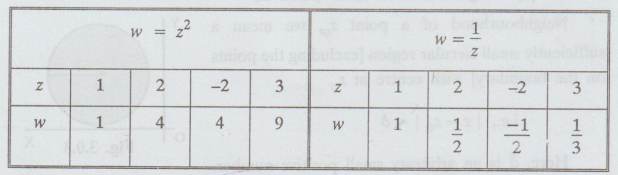
Example: w = z2, w = 1/z

Note (ii) Multiple - valued function

If there is more than one value of w corresponding to a given value of z, then w is called a multiple - valued function.

Example: w = z^1/2

Note (iii) The distance between two points z

and z_o is | z - z_o |

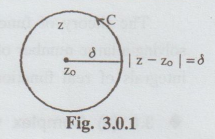
Note (iv) The circle C of radius δ with centre at the point z_o can be represented by

| z - z_o | = δ

Note (v) | z - z_o | δ represents the interior of the circle excluding its circumference.

Note (vi) | z - z_o | ≤ δ represents the interior of the circle including its circumference

Note (vii) | z - z_o | > δ represents the exterior of the circle

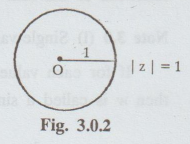
Note (viii) A circle of radius 1 with centre at origin can be represented by | z | = 1

(c) Neighbourhood of a point z_o

Neighbourhood of a point z_o we mean a sufficiently small circular region [ excluding the points on the boundary with centre at z_o

i.e., | z - z_o | < δ

(d) Limit of a Function

Let f (z) be a single valued function defined at all points in some neighbourhood of point z_o.

Then the limit of f (z) as z approaches z_o is w_o

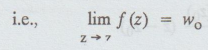
 (e) Continuity

If f (z) is said to be continuous at z = z_o, then

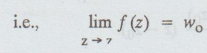
Note (ix) If two functions are continuous at a point their sum, difference and product are also continuous at that point, their quotient is also continuous at any such point [dr ≠ 0]

Example 3.0.1 State the basic difference between the limit of a function of a real variable and that of a complex variable. [A.U M/J 2012]

Solution :

In real variable, x→x_o implies that x approaches xo along the X-axis (or) a line parallel to the X-axis.

In complex variables, z → z_o implies that z approaches zo along any path joining the points z and z₀ that lie in the z-plane.

(f) Differentiability at a point

A function f (z) is said to be differentiable at a point z = z_o, if the limit

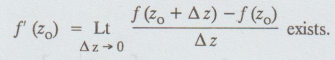
This limit is called the derivative of f (z) at the point z = z_o

Note (x). If f (z) is differentiable at zo, then f(z) is continuous at Z_o. This is the necessary condition for differentiability.

Example 3.0.2 If f (z) is differentiable at zo, then show that it is continuous at that point.

Solution :

As f (z) is differentiable at zo both f (z₀) and f' (z₀) exist finitely.

This is exactly the statement of continuity of f (z) at z₀.

Example 3.0.3. Give an example to show that continuity of a function at a point does not imply the existence of derivative at that point.

Solution :

Consider the function w= | z |² = x² + y²

This function is continuous at every point in the plane, being a continuous function of two real variables. However, this is not differentiable at any point other than origin.

Example 3.0.4. Show that the function f (z) is discontinuous at z = 0, given that 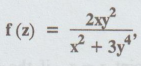when z ≠ 0 and f (0) = 0.

Solution:

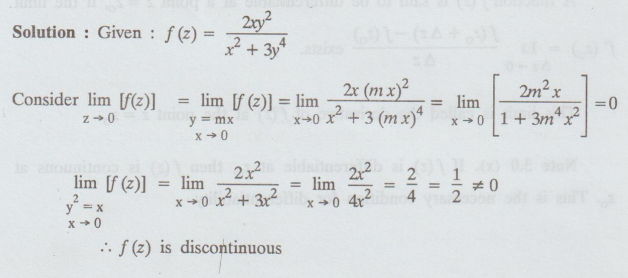
Example 3.0.5. Show that the function f(z) is discontinuous at the origin (z = 0), given that f(z) =  xy (x-2y) / x³ + y³ when z ≠ 0

= 0, when z = 0.

Solution :