Anna University Long Questions and Answers

Unit - III

Chapter 3

Phase Rule

Anna University Long Questions & Answers

 

PART - B

1. State phase rule and explain the terms involved in it. (TNV A.U. May 2009)(A.U. June 2009, June 2014)

If the equilibrium between any number of phases is not influenced by gravity, or electrical, or magnetic forces but is influenced only by pressure, temperature and concentration, then the number of degree of freedom (F) of the system is related to number of components (C) and number of phases (P) by the following phase rule equation.

F = C – P + 2

Explanation (or) meanings of terms

(a) Phase (P)

Phase is defined as, “any homogeneous physically distinct and mechanically separable portion of a system which is separated from other parts of the system by definite boundaries”.

Example

Gaseous phase

All gases are completely miscible and there is no boundary between one gas and the other.

Example

Air, which is a mixture of O₂, H₂, N₂, CO₂ and water vapour, etc., constitutes a single phase.

(b) Component (C)

Component is defined as, “the smallest number of independently variable constituents, by means of which the composition of each phase can be expressed in the form of a chemical equation".

Example

Consider a water system consisting of three phases.

Ice(s) ⇌ Water(1) ⇌ Vapour(g)

The chemical composition of all the three phases is H₂O, but are in different physical form. Hence the number of component is one.

(c) Degree of freedom (F)

Degree of freedom is defined as, “the minimum number of independent variable factors such as temperature, pressure and concentration, which must be fixed in order to define the system completely".

Example

Consider the following equilibrium

Ice(s) ⇌ Water(l) ⇌F apour(g)

These three phases will be in equilibrium only at a particular temperature and pressure. Hence, this system does not have any degree of freedom, so it is non variant or zero variant.

 

2. Draw a neat one component water system and explain in detail. (A.U. Jan 2014, Dec 2016, May 2017)

Water exists in three possible phases namely solid, liquid and vapour. Hence, there can be three forms of equilibria.

Solid ⇌ Liquid

Liquid ⇌ Vapour

Solid ⇌ Vapour

Each of the above equilibrium involves two phases. The phase diagram for the water system is shown in the following figure.

This phase diagram contains curves, areas, and triple point.

(a) Curve OA

The curve OA is called vapourisation curve, it represents the equilibrium between water and vapour. At any point on the curve the following equilibrium will exist.

Water ⇌ Water vapour

The degree of freedom of the system is one, i.e., univariant. This is predicted by the phase rule.

F = C – P + 2; F = 1 – 2 + 2; F = 1

This equilibrium (i.e. line OA) will extend upto the critical temperature (374°C). Beyond the critical temperature the equilibrium will disappear only water vapour will exist.

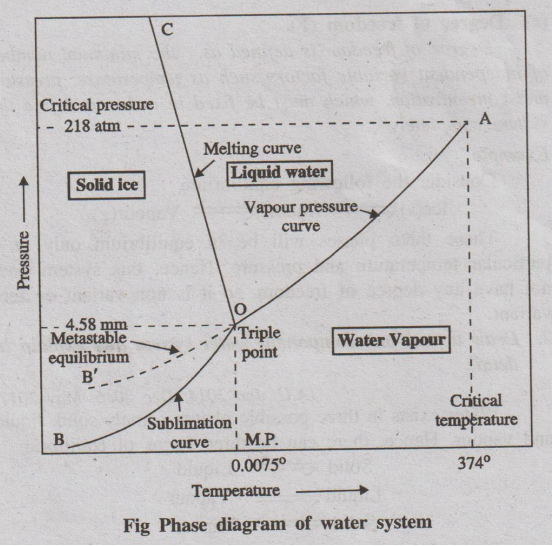
Fig Phase diagram of water system

(b) Curve OB

The curve OB is called sublimation curve of ice, it represents the equilibrium between ice and vapour. At any point on the curve the following equilibrium will exist.

Ice ⇌ Vapour

The degree of freedom of the system is one, i.e. univariant. This is predicted by the phase rule.

F = C – P + 2; F = 1 – 2 + 2; F = 1

This equilibrium (line OB) will extend upto the absolute zero (-273°C), where no vapour can be present and only ice will exist.

(c) Curve OC

The curve OC is called melting point curve of ice, it represents the equilibrium between ice and water. At any point on the curve the following equilibrium will exist.

Ice ⇌ water

The curve OC is slightly inclined towards pressure axis. This, shows that melting point of ice decreases with increase of pressure.

The degree of freedom of the system is one, i.e., univariant.

(d) Point ‘O' (Triple point)

The three curves OA, OB and OC meet at a point 'O’, where three phases namely solid, liquid and vapour are simultaneously at equilibrium.

This point is called triple point, at this point the following equilibrium will exist.

Ice(s) ⇌ Water(1) ⇌ Vapour(g)

The degree of freedom of the system is zero i.e., nonvariant. This is predicted by the phase rule.

F = C - P + 2; F = 1 - 3 + 2; F = 0

Temperature and pressure at the point “O' are 0.0075°C and 4.58 mm respectively.

(e) Curve OB': (Metastable equilibrium)

The curve OB' is called vapour pressure curve of the super-cool water or metastable equilibrium where the following equilibrium will exist.

Super-cool water ⇌ Vapour

(f) Areas

Area AOC, BOC, AOB represents water, ice and vapour respectively. The degree of freedom of the system is two. i.e.. Bivariant.

This is predicted by the phase rule

F = C - P + 2; F = 1 - 1 + 2; F = 2

 

3. Draw a neat phase diagram and explain the lead-silver system? Briefly write about Pattinson's process. (A.U. May 2003, June 2014, Dec 2016)

Since the system is studied at constant pressure, the vapour phase is ignored and the condensed phase rule is used.

F' = C – P + 1

The phase diagram of lead-silver system is shown in the following figure. It contains lines, areas and the eutectic point.

(a) Curve AO

The curve AO is known as freezing point curve of silver. Point A is the melting point of pure Ag (961°C). The curve AO shows the melting point depression of Ag by the successive addition of Pb. Along this curve AO, solid Ag and the melt are in equilibrium. S

olid Ag ⇌ Melt

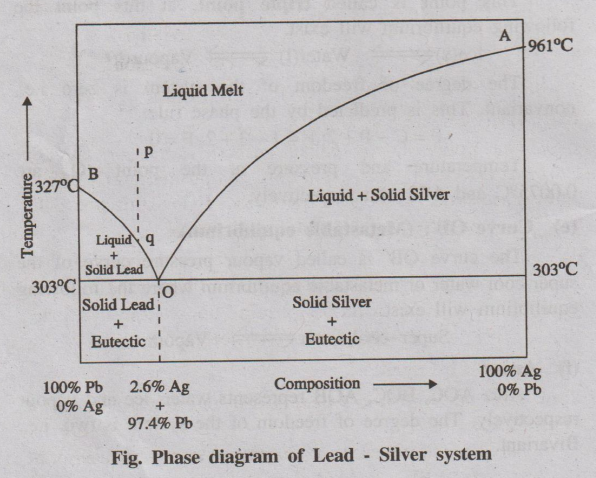
Fig. Phase diagram of Lead - Silver system

According to reduced phase rule equation.

F' = C – P + 1; F' = 2 - 2 + 1; F' = 1

The system is univariant.

(b) Curve BO

The curve BO is known as freezing point curve of lead. Point B is the melting point of pure lead (327°C). The curve BO shows the melting point depression of ‘Pb' by the successive addition of ‘Ag’. Along this curve ‘BO’, solid ‘Pb' and the melt are in equilibrium.

Solid Pb ⇌ Melt

According to reduced phase rule equation.

F' = C - P +1; F' = 2 - 2 + 1; F' = 1

The system is univariant

(c) Point 'O' (Eutectic point)

The curves AO and BO meet at point 'O' at a temperature of 303°C, where three phases (solid Ag, solid Pb and their liquid melt) are in equilibrium.

Solid Pb + Solid Ag ⇌ Melt.

According to reduced phase rule equation.

F' = C - P + 1; F' = 2 - 3+1; F' = 0

The system is non-variant.

The point “O' is called eutectic point or eutectic temperature and its corresponding composition, 97.4%Pb + 2.6%Ag, is called eutectic composition. Below this point the eutectic compound and the metal solidify.

(d) Areas

The area above the line AOB has a single phase (molten Pb + Ag). According to reduced phase rule equation.

F' = C - P + 1; F' = 2 - 1 + 1; F' = 2

The system is bivariant.

Application of Pattinson's process for the desilverisation of Argentiferous lead

The argentiferous lead, consisting of a very small amount of silver (say 0.1%), is heated to a temperature above its melting point, so that the system consisting of only the liquid phase represented by the point ‘p' in the above figure. It is then allowed to cool. The temperature falls down along the line 'pq'. As soon as the point 'q' is reached, Pb is crystallised out and the solution will contain relatively increasing amount of ‘Ag’. On further cooling, more and more ‘Pb' is separated along the line ‘BO’ the melt continues to be richer and richer in silver until the point O is reached, where the percentage of • Ag rises to 2.6%.

Thus, the process of raising the relative proportion of Ag in the alloy is known as Pattinson's process.

 

 4. Mention the limitations of phase rule. (A.U. Dec 2008)

(a) Phase rule can be applied only for the systems in equilibrium.

(b) Only three variables like P, T & C are considered, but not electrical, magnetic and gravitational forces.

(c) All the phases of the system must be present under the same conditions of pressure and temperature.

(d) Solid and liquid phases must not be in finely divided state, otherwise deviations occur.

 

5. What is condensed phase rule? What is the number of degrees of freedom at the eutectic point for a two component system? (AU. May 2003, June 2006)

A solid-liquid equilibrium of an alloy has practically no gaseous phase and the effect of pressure is negligible. Therefore, experiments are conducted under atmospheric pressure. Thus the system in which only the solid and liquid phases are considered and the gas phase is ignored is called a condensed system. Since the pressure is kept constant, the phase rule becomes

F' = C – P + 1.

This equation is called reduced phase rule or condensed phase rule.

Example

Consider a two component solid Pb - solid Ag system, the following equilibrium will exist at eutectic point “0’

Solid Pb + Solid Ag ⇌ melt

Number of Phases = 3

Number of components = 2

:: F' = C – P + 1

= 2 - 3 + 1

F' = 0

Number of degree of freedom = 0 (zero)

 

6. What is thermal analysis. Draw the cooling curves of a pure substance and a mixture and discuss. (AU. June 2006)

Thermal analysis is a method involving a study of the cooling curves of various compositions of a system during solidification. The shapes of the freezing point curves for any system (involving metals) can be determined by thermal analysis. The form of the cooling curve indicates the composition of the solid.

Example - 1 Cooling curve for a pure solid

A pure substance in the fused state is allowed to cool slowly and the temperature is noted at different time interval. Then graph is plotted between temperature and time (Fig.(a)).

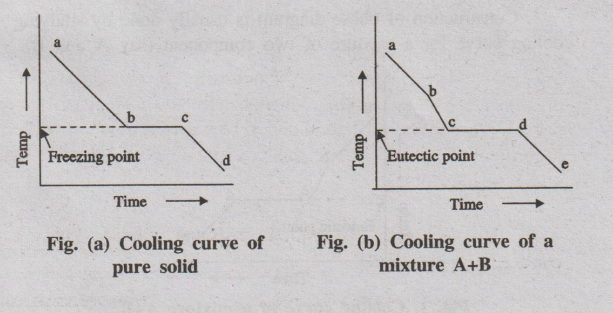
Fig. (a) Cooling curve of

Fig. (b) Cooling curve of a

Initially the rate of cooling is continuous. When it reaches the point ‘b'solid begins to appear, now the temperature remains constant until the liquid melt is completely solidified. Solidification completes at the point 'c'. The horizontal line ‘bc' represents the equilibrium between the solid and liquid melt. After the point 'c', temperature of the solid begins to decrease along the curve 'cd'.

Example - 2 Cooling curve for a mixture

If a mixture of two substances (say A and B) in the fused state is allowed to cool slowly, the cooling curve is obtained in a similar manner (Fig. (b)).

Initially the rate of cooling is continuous. When it reaches the point b'one substance (either A or B) begins to solidify out of the melt, which is indicated by a break and the rate of cooling is different. On further cooling at the break point ‘c'the second compound also begins to solidify. Now the temperature remains constant until the liquid melt is completely solidified, which forms the eutectic mixture (line cd). After the break point d' cooling of solid mass begins. The temperature of horizontal line 'cd' gives the eutectic temperature.

 

7. Explain the construction of phase diagram with neat sketch.

Construction of phase diagram is usually done by studying cooling curve for a mixture of two component (say A and B).

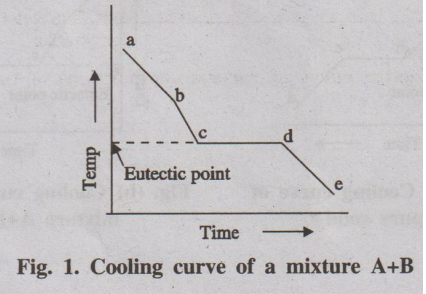
Fig. 1. Cooling curve of a mixture A+B

If a mixture of two substances (say A and B) in the fused state is allowed to cool slowly, the cooling curve is obtained in a similar manner (Fig. 1).

Initially the rate of cooling is continuous. When it reaches the point 'b' one substance (either A or B) begins to solidify out of the melt, which is indicated by a break and the rate of cooling is different. On further cooling at the break point 'c' the second compound also begins to solidify. Now the temperature remains constant until the liquid melt is completely solidified, which forms the eutectic mixture (line cd). After the break point d' cooling of solid mass begins. The temperature of horizontal line 'cd' gives the eutectic temperature.

The experiment is repeated for different compositions of A and B and the various cooling curves are recorded. From the cooling curves of various compositions, the main phase diagram can be drawn by taking composition in X-axis and the temperature in Y-axis. (Fig. 2)

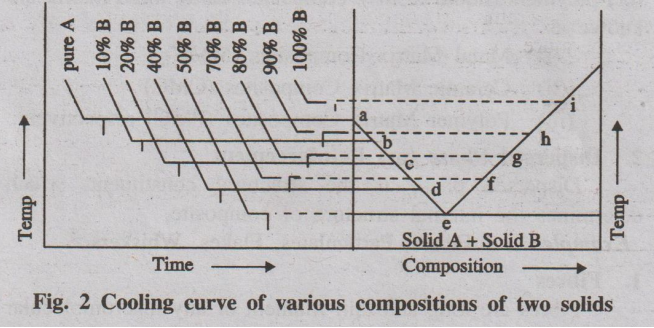
Fig. 2 Cooling curve of various compositions of two solids