Applications of Ampere's Circuital Law

Applications of Ampere's Circuital Law

AU : Dec.-02, 06, 07, 14, 16, 18, May-04, 13, 14, 16, 19

• Let us study the various cases and the application of Ampere's circuital law to obtain  .

1.   due to Infinitely Long Straight Conductor

• Consider an infinitely long straight conductor placed along z-axis, carrying a direct current I as shown in the Fig. 7.9.1. Consider the Amperian closed path, enclosing the conductor as shown in the Fig. 7.9.1. Consider point P on the closed path at which   is to be obtained. The radius of the path is r and hence P is at a perpendicular distance r from the conductor. 

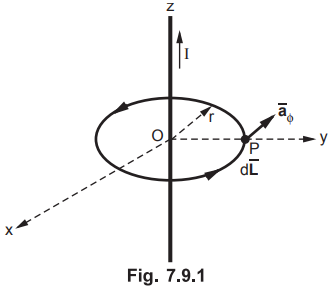
• The magnitude of  depends on r and the direction is always tangential to the closed path i.e. . So  has only component in  direction say Hϕ

• Consider elementary length  at point P and in cylindrical co-ordinates it is  direction.

2.   due to a Co-axial Cable

• Consider a co-axial cable as shown in the Fig. 7.9.2. Its inner conductor is solid with radius a, carrying direct current I. The outer conductor is in the form of concentric cylinder whose inner radius is b and outer radius is c. This cable is placed along z axis. The current I is uniformly distributed in the inner conductor. While - I is uniformly distributed in the outer conductor.

• The space between inner and outer conductor is filled with dielectric say air. The calculation of   is divided corresponding to various regions of the cable.

Region 1 : Within the inner conductor, r < a. Consider a closed path having radius r < a. Hence it encloses only part of the conductor as shown in the Fig. 7.9.3.

• The area of cross-section enclosed is πr² m².

• The total current flowing is I through the area πa². Hence the current enclosed by the closed path is,

• The   is again only in  direction and depends only on r.

Region 2 : Within a < r < b consider a circular path which encloses the inner conductor carrying direct current I. This is the case of infinitely long conductor along z-axis. Hence  in this region is,

Region 3 : Within outer conductor, b < r < c

• Consider the closed path as shown in the Fig. 7.9.4.

The current enclosed by the closed path is only the part of the current - I, in the outer conductor. The total current - I is flowing through the cross section π (c² -b²) while the closed path encloses the cross section π (r² - b²).

• Hence the current enclosed by the closed path of outer conductor is,

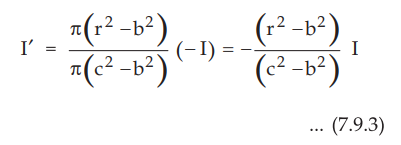
Key Point : Note that the closed path also encloses the inner conductor hence the current I flowing though it.

I'' = I = Current in inner conductor enclosed        ... (7.9.4)

Total current enclosed by the closed path is,

According to Ampere's circuital law,

Region 4 : Outside the cable, r > c.

• Consider the closed path with r > c such that it encloses both the conductors i.e. both currents + I and - I. 

• Thus the total current enclosed is,

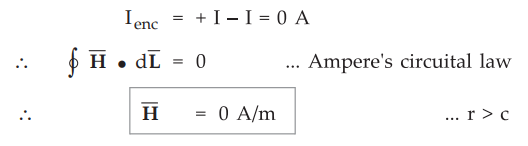
• The magnetic field does not exist outside the cable. The variation of  against r is shown in the Fig. 7.9.5.

1.  due to Infinite Sheet of Current

• Consider an infinite sheet of current in the z = 0 plane. The surface current density is . The current is flowing in positive y direction hence . This is shown in the Fig. 7.9.6.

 • Consider a closed path 1-2-3-4 as shown in the Fig. 7.9.6. The width of the path is b while the height is a. It is perpendicular to the direction of current hence in xz plane.

• The current flowing across the distance b is given by K_yb.

I_enc = K_yb

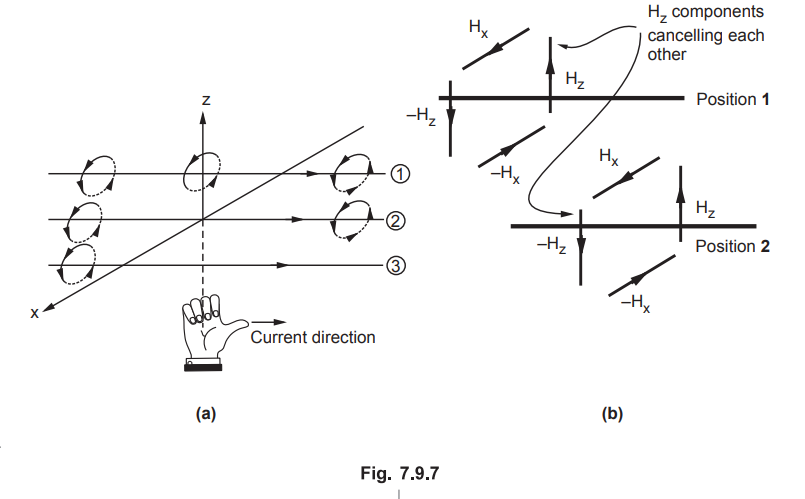
• Consider the magnetic lines of force due to the current in  direction, according to right hand thumb rule. These are shown in the Fig. 7.9.7.

• In Fig. 7.9.7 (b), it is clear that in between two very closely spaced conductors, the components of  in z direction are oppositely directed (- Hz for position 1 and + Hz for position 2 between the two positions). All such components cancel each other and hence  can not have any component in z direction.

Evaluate the integral along the path 1-2-3-4-1.

• The path 2-3 is lying in z < 0 region for which  is And limits from 2 to 3, positive x to negative x hence effective sign of the integral is positive.

Ex. 7.9.1 Obtain the expression for   in all the regions if a cylindrical conductor carries a direct current I and its radius is 'R' m. Plot the variation of   against the distance r from the centre of the conductor.

AU : Dec.-14, 16, Marks 10

Sol. : Let the cylindrical conductor of radius R, carries a uniform direct current of I A. It is placed along z axis and has infinite length.   is to be obtained considering two regions.

Region 1 : Within the conductor, r < R.

Consider the closed path of radius r within the conductor as shown in the Fig. 7.9.8.

As current I flows uniformly, it flows across the cross-sectional area of πR²

While the closed path encloses only part of the current which passes across the cross-sectional area of πr²

Hence current enclosed by the path,

Region 2 : Outside the conductor, r > R.

The conductor is infinite length along z axis carrying direct current I hence using the earlier result,

The graphical variation of   against r measured from centre of the conductor is shown in the Fig. 7.9.9.

Ex. 7.9.2 The plane y = 1 carries current density

Sol. : The sheet is located at y = 1 on which  is in  direction. The sheet is infinite and is shown in the Fig. 7.9.10.

This is to the right of the plane as y = 5 for B.

Ex. 7.9.3 A 'z' directed current distribution is given by, 

Find   at any point r ≥ a using Ampere's circuital law.

AU : May-19, Marks 13

Sol. : As current density is given,

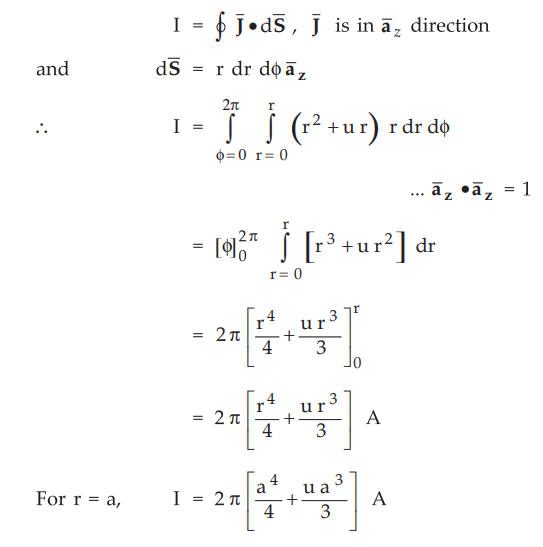
Consider a closed path with r > a which is Amperian path.

Ex. 7.9.4 A long cylindrical wire has a current density flowing in the direction of its length whose density is J= Jor, where r is the distance from the cylinder's axis. Find the magnetic field both inside and outside the cylinder.

Sol. : Let the radius of the cylinder is R. It is placed along z-axis.   to be obtained for two regions, r > R and r < R.

The total current in the wire can be obtained by integrating current density over its cross-section.

The closed path of radius r within the conductors is selected.

Ex. 7.9.5 A steady current of 1000 A is established in a long straight, hollow aluminium conductor of inner radius 1 cm and outer radius 2 cm. Assuming uniform resistivity, calculate   as a function of radius r from the axis of the conductor.

Sol. : Consider the conductor as shown in the Fig. 7.9.12.

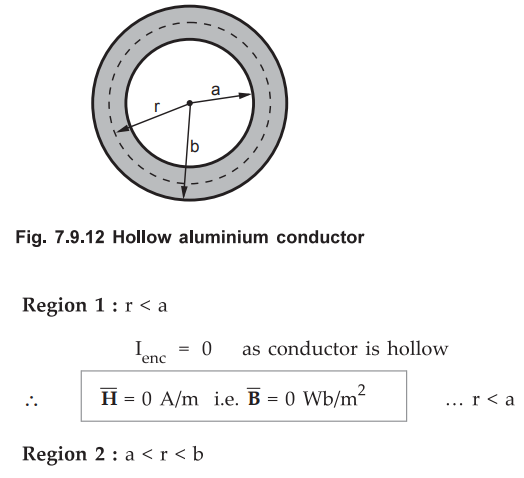
Consider the cross-section upto radius r as shown in the Fig. 7.9.12.

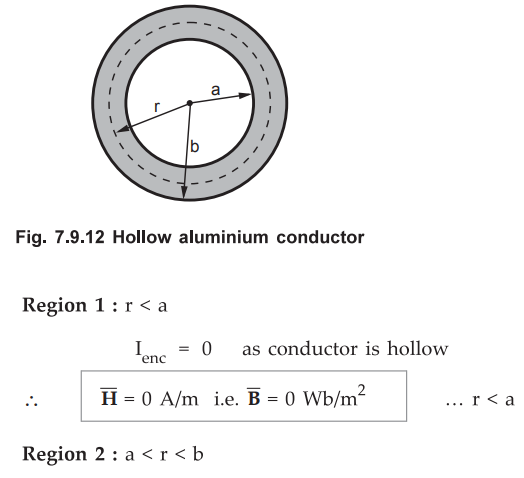
The total current I flows through the area π [b² - a²].

Hence the current enclosed by the closed path is,

The variation of   against r is shown in the Fig. 7.9.13.

Ex. 7.9.6 A current filament of 5.0 A in the  direction is parallel to the y-axis at x = 2 m, z = - 2 m. Find  at the origin.

Sol. : The filament is shown in the Fig. 7.9.14.

Review Questions

1. Find the magnetic field intensity due to infinitely long straight conductor using Ampere's circuital law.

2. Deduce the expression for magnetic field intensity due to a coaxial cable carrying current I.

AU : May-14, Marks 16

3. Using Ampere's circuital law, find magnetic field intensity due to infinite sheet of current.

AU : Dec.-02, 06, 07, May-04, Marks 10, May-13, Marks 6

4. Discuss the applications of Ampere's circuital law.

5. Develop an expression for the magnetic field intensity at any point on the line through the centre at a distance 'h' m from the centre and perpendicular to the plane of a circular loop (in XY plane) of radius 'a'm and carrying a current 1 Ampere in the anti-clockwise