Applications of Gauss's Law

Applications of Gauss's Law

AU ; Dec.-02, 03, 04, 05, 08, 11, 14, 17, May-05, 06, 08, 17,18

• The Gauss's law is infact the alternative statement of Coulomb's law. The Gauss's law can be used to find  or  for symmetrical charge distributions, such as point charge, an infinite line charge, an infinite sheet of charge and a spherical distribution of charge. The Gauss's law is also used to find the charge enclosed or the flux passing through the closed surface. Note that whether the charge distribution is symmetrical or not, Gauss's law holds for any closed surface but can be easily applied to the symmetrical distributions. But the Gauss's law cannot be used to find  r  if the charge distribution is not symmetric.

•While selecting the closed Gaussian surface to apply the Gauss's law, following conditions must be satisfied,

1.   is every where either normal or tangential to the closed surface i.e. . becomes D dS or zero respectively.

2.    is constant over the portion of the closed surface for  is not zero.

• Let us apply these ideas to the various charge distributions.

 

1. Point Charge (Proof of Gauss's Law)

• Let a point charge Q is located at the origin.

• To determine   and to apply Gauss's law, consider a spherical surface around Q, with centre as origin. This spherical surface is Gaussian surface and it satisfies required condition. The  is always directed radially outwards along  which is normal to the spherical surface at any point P on the surface. This is shown in the Fig. 3.7.1.

• Consider a differential surface area dS as shown. The direction normal to the surface dS is , considering spherical co-ordinate system. The radius of the sphere is r = a. 

• The direction of  is along which is normal to dS at any point P.

• In spherical co-ordinate system, the dS normal to radial direction  is,

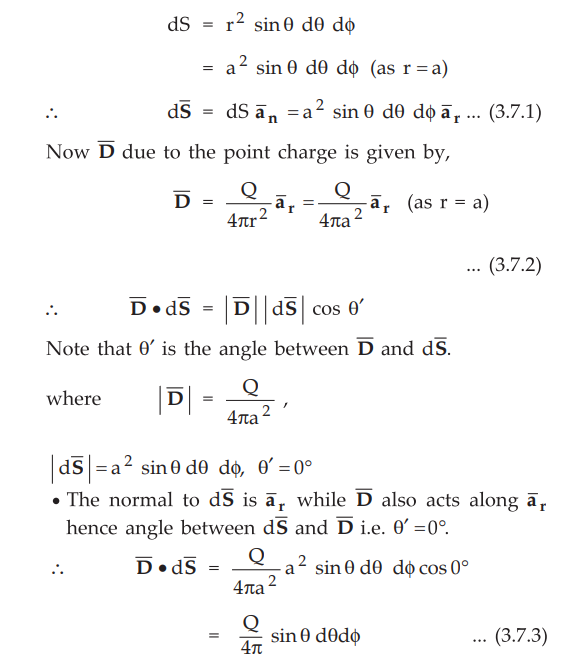
• Alternatively to avoid the confusion between the symbol θ we can write,

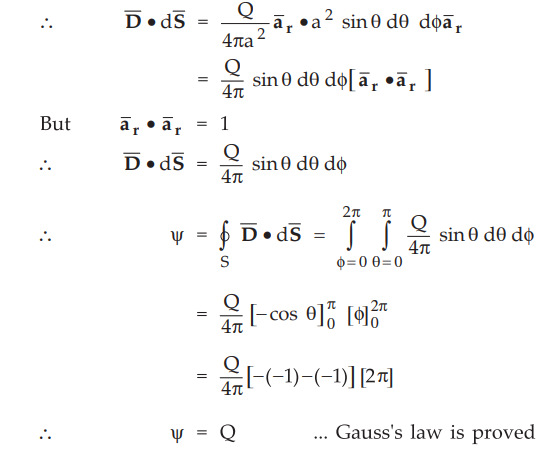
• This proves the Gauss's law that Q coulombs of flux crosses the surface if Q coulombs of charge is enclosed by that surface.

Key Point : As  is obtained from the result of   which is obtained from Coulomb's law, it can be said that the above discussion is the proof of Gauss's law from the Coulomb's law.

a. Use of Gauss's Law to Obtain 

• Alternatively Gauss's law can be used to obtain . Let us see how -

• From Gauss's law,

1. Identify |   | and its direction.

2. Identify and direction normal to dS.

3. Take dot product,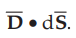 

4. Choose the Gaussian surface.

5. Integrate over the surface chosen as Gaussian surface, keeping |   | unknown as it is.

6. Find charge Q enclosed by Gaussian surface.

7. Equate the charge Q, to the integration obtained with |   | as unknown.

8. Determine |   | and express   with its direction. Then

• For a sphere of radius r, the flux density   is in radial direction

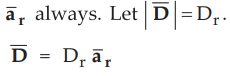
• Let the Gaussian surface is a sphere of radius r enclosing charge Q. 

• While for the Gaussian surface i.e. sphere of radius r, dS normal to is,

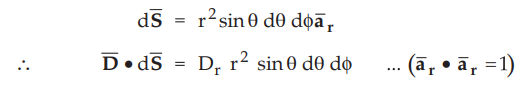
• Now integrate over the surface of sphere of constant radius ’r'.

The expressions are same as those obtained by Coulomb's law, earlier in the Chapter-2.

This is the use of Gauss's law to obtain  for a given charge distribution.

Note : Symmetry helps us to apply Gauss's law for the given situation. To understand symmetry, obtain the information,

1. With which co-ordinates does the  vary ?

2. Which components of  are present ?

• This results into simpler integration to be solved to obtain the required result.

 

2. Infinite Line Charge

• Consider an infinite line charge of density ρL C/m lying along z-axis from - ∞ to + ∞. This is shown in the Fig. 3.7.2.

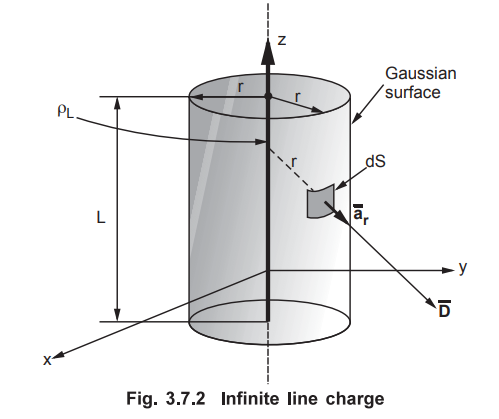
• Consider the Gaussian surface as the right circular cylinder with z-axis as its axis and radius r as shown in the Fig. 3.7.2. The length of the cylinder is L.

• The flux density at any point on the suface is directed radially outwards i.e in the   direction according to cylindrical co-ordinate system.

• Consider differential surface area dS as shown which is at a radial distance r from the line charge. The direction normal to dS is  

• As the line charge is along z-axis, there can not be any component of  in z direction. So  has only radial component.

• The integration is to be evaluated for side surface, top surface and bottom surface.

• Now D_r is constant over the side surface.

• As  has only radial component and no component along  hence integrations over top and bottom surfaces is zero.

• The results are same as obtained from the Coulomb's law.

 

3. Coaxial Cable

• Consider the two coaxial cylindrical conductors forming a coaxial cable. The radius of the inner conductor is 'a' while the radius of the outer conductor is 'b'. The coaxial cable is shown in the Fig. 3.7.3. The length of the cable is L.

• The charge distribution on the outer surface of the inner conductor is having density ρS C'/m². The total outer surface area of the inner conductor is 2 π aL.

• Hence ρs can be expressed interms of p L

ρL = ρ_S  × Surface area / Total length

= ρ_S  × 2πaL / L

ρL = 2πa ρ_S C/m

• Thus the line charge density of inner conductor is ρL C/m.

• Consider the right circular cylinder of length L as the Gaussian surface. Due to the symmetry,   has only radial component. From the discussion of line charge we can write,

Q = D_r 2π rL         ...(3.7.5)

where          a < r < b ... Refer equation (3.7.4)

• The total charge on the inner conductor is to be obtained by evaluating the surface integral of the surface charge distribution.

• This is same as obtained for infinite line charge. Every flux line starting from the positive charge on the inner cylinder must terminate on the negative charge on the inner surface of the outer cylinder. Hence the total charge on the inner surface of the outer cylinder is,

But

Q_{outer cylinder} = 2 π a L ρ_S(inner) ... (3.7.13)

Q_{outer cylinder} = 2 π a L ρ_S(outer) ... (3.7.14)

2π bL ρ_S(outer) = - 2π a L ρ_S(inner)

ρ_S(outer) = - a / b ρ_S(inner)   ... (3.7.15)

• If the Gaussian surface is considered such that r > b, then the total charge enclosed will be zero as equal and opposite charges on the cylinder will cancel each other.

• Similarly inside the inner cylinder, r < a also the total charge enclosed will be zero.

 

4. Infinite Sheet of Charge

• Consider the infinite sheet of charge of uniform charge density ρ_S C/m², lying in the z = 0 plane i.e. xy plane as shown in the Fig. 3.7.4.

• Consider a rectangular box as a Gaussian surface which is cut by the sheet of charge to give dS = dx dy.

• The results are same as obtained by the Coulomb's law for the infinite sheet of charge. 

 

5. Spherical Shell of Charge

• Consider an imaginary spherical shell of radius ’a’.

• The charge is uniformly distributed over its surface with a density ρS C/m². Let us find   at a point P located at a distance r from the centre such that r > a and r ≤ a, using Gauss's law.

• The shell is shown in the Fig. 3.7.5.

Case 1 : Point P outside the shell (r > a)

• Consider a point P at a distance r from the origin such that r > a. The Gaussian surface passing through point P is a concentric sphere of radius r. Due to spherical Gaussian surface, the flux lines are directed radially outwards and are normal to the surface. Hence electric flux density  is also directed radially outwards at point P and has component only in  direction. Consider a differential surface area at P normal to  direction hence dS = r ²sin θ d θ d ϕ in spherical system.

• Thus for r > a, the field E is inversely proportional to the square of the distance from the origin.

If the surface charge density is ρs C/m² then

Case 2 : Point P is on the shell ( r = a)

On the shell, r = a

• The Gaussian surface is same as the shell itself and   can be obtained using r = a in the equation (3.7.20).

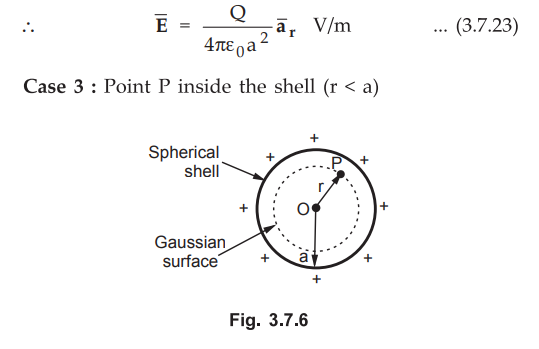
• The Gaussian surface, passing through the point P is again a spherical surface with radius r < a.

• But it can be seen that the entire charge is on the surface and no charge is enclosed by the spherical shell. And when the Gaussian surface is such that no charge is enclosed, irrespective of any charges present outside, the total charge enclosed is zero. 

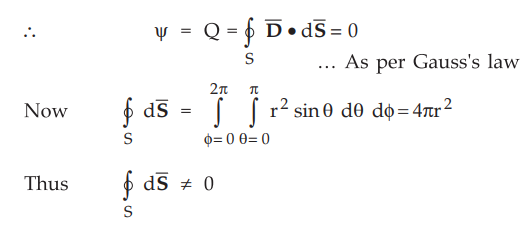
Hence to satisfy that total charge enclosed is zero, inside the spherical shell.

• Thus electric flux density and electric field at any inside a spherical shell is zero.

a. Variation of   against r

• The variation of    against the radial distance r measured from the origin is shown in the Fig. 3.7.7.

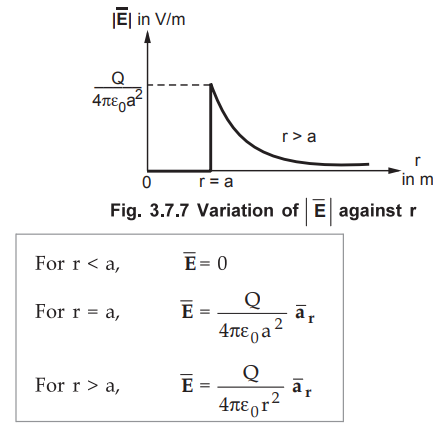
• After r = a, the    is inversely proportional to the square of the radial distance of a point from the origin. The variation of |   | against r is also similar. For the medium other than the free space, £ o must be replace d by Ɛ = Ɛ₀ Ɛ_r

 

6. Uniformly Charged Sphere

• Consider a sphere of radius 'a' with a uniform charge density of ρv C/m³. Let us find  at a point P located at a radial distance r from centre of the sphere such that r ≤ a and r > a, using Gauss's law.

• The sphere is shown in the Fig. 3.7.8.

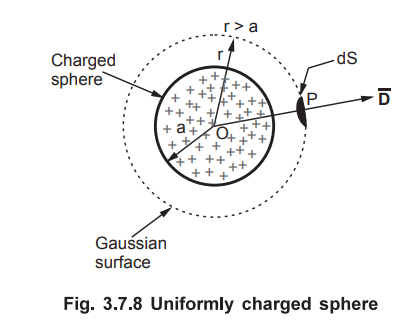
Case 1 : The point P is outside the sphere (r > a).

• The Gaussian surface passing through point P is a spherical surface of radius r.

• The flux lines and  are directed radially outwords along   direction.

• The differential area dS is considered at point P which is normal to direction.

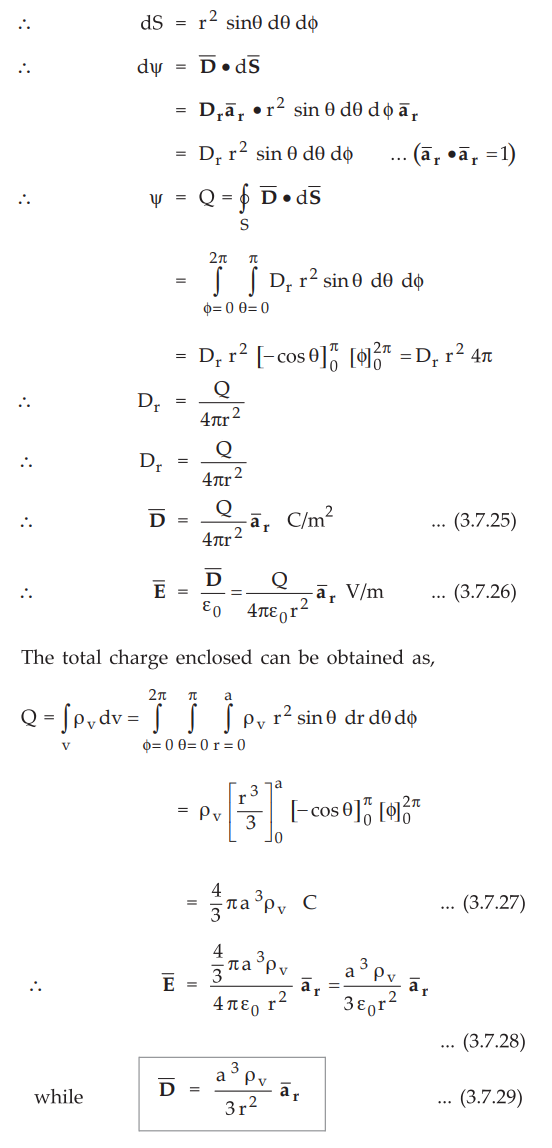
• These are the expressions for   outside the uniformly charged sphere.

Case 2 : The point P on the sphere (r = a).

• The Gaussian surface is same as the surface of the charged sphere. Hence results can be obtained directly substituting r = a in the equation (3.7.28) and (3.7.26).

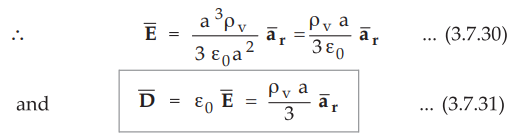
Case 3 : The piont P is inside the sphere (r < a) the Gaussian surface is a spherical surface of radius r where r < a.

• Consider differential surface area dS as shown in the Fig. 3.7.9.

• Now the charge enclosed is by the sphere of radius r only and not by the entire sphere. The charge outside the Gaussian surface will not affect   .

Key Point : The results obtained here can be used as the standard results while solving the problems.

• If the sphere is in a medium of permittivity Ɛ_r then Ɛ₀ must be replaced by Ɛ = Ɛ₀ Ɛ_r

a. Variation of   against r

• From the equations (3.7.26), (3.7.28) and (3.7.33) it can seen that for r > a, the  is inversely proportional to square of the distance while for r < a it is directly proportional to the distance r.

• At r = a, 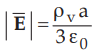 = depends on the radius of the charged sphere.

• For r > a, the graph of |  | against r is parabolic while for r < a it is a straight line as shown in the Fig. 3.7.10.

• The graph of | | against r is exactly similar in nature as |   | against r.

 

Ex. 3.7.1 A charge configuration is given by, ρv = 5re^-2r (c/ m³). Find  using Gauss's law.

Sol. : Assume given ρ v is in cylindrical co-ordinates. Let the Gaussian surface be a right circular cylinder of length L and radius r, with z axis as its axis, as shown in the Fig. 3.7.11. The charge density is a function of r alone hence flux is in radial direction and  also is directed radially outwards.

Consider the differential surface area dS normal to   direction.

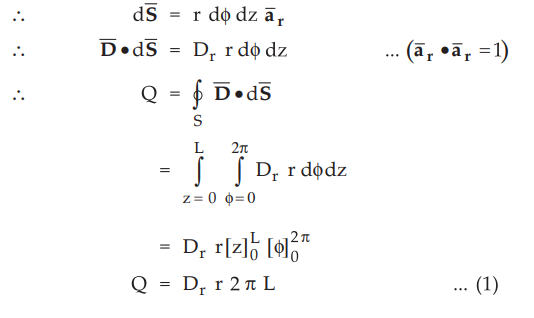
Let us find charge enclosed by right circular cylinder of length L.

 

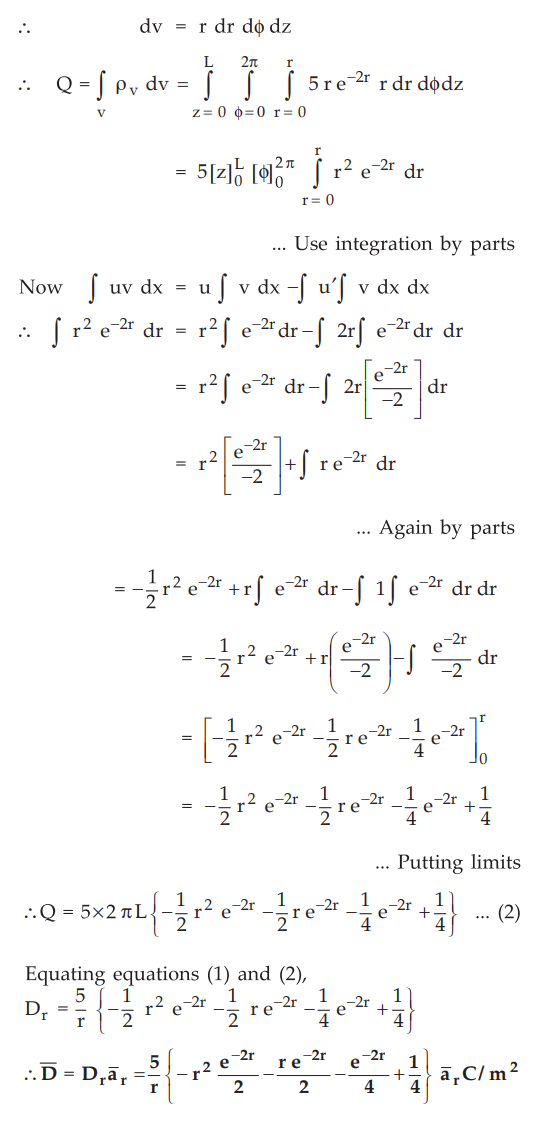
Ex. 3.7.2 Three charged cylindrical sheets are present in three spaces with ρ = 5 c/m² at R = 2 m, ρ = - 2C/m² at R = 4m and ρ = - 3C/m² at R = 5 m. Find flux density at R = 1, 3, 4.5 and 6 m.

Sol. : The charge enclosed by the cylinder is given by,

 

Ex. 3.7.3 The electric flux density is given as   in free space. Calculate :

1) The electric field intensity at r = 0.25 m

2) The total charge within a sphere of r = 0.25 m and

3) The total flux leaving the sphere ofr = 0.35 m.

AU : Dec.-08, Marks 10

Sol.:

 

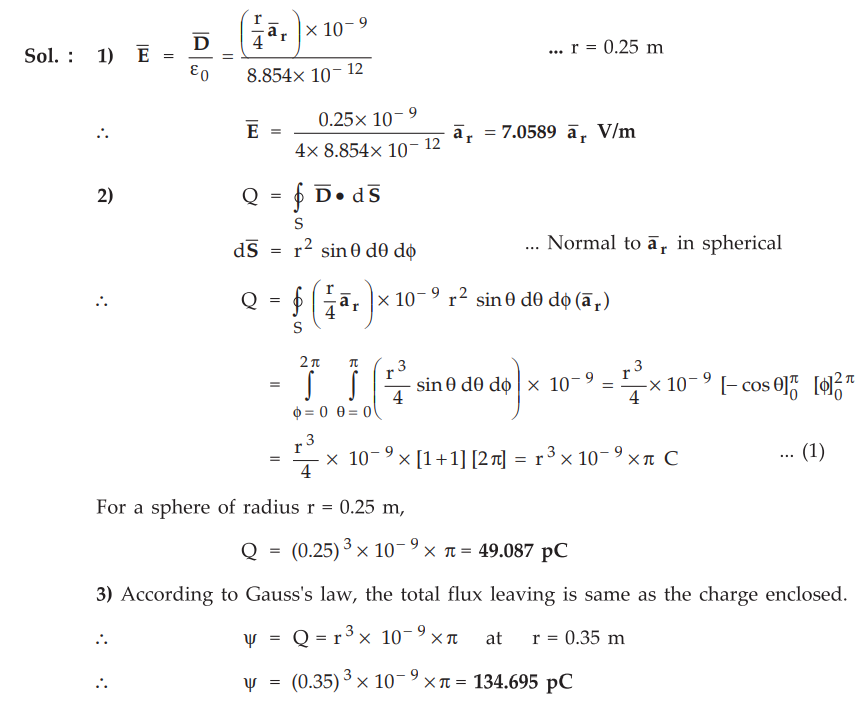
Ex. 3.7.4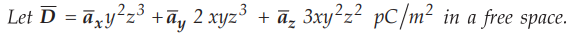 

Find i) Total electric flux passing the surface x = 3, 0 ≤ y ≤ 2, 0 ≤ z ≤ 1 in a direction away from the origin, ii) |   | at a point P (3, 2, 1).

Sol. :

 

Ex. 3.7.5 A 50 cm length coaxial cable having an inner radius 1 mm and an outer radius 4 mm, has its inner space between the conductors filled with air. The total charge on the inner conductor is 30 nC. Find the charge density on each conductor.

Sol. :

 

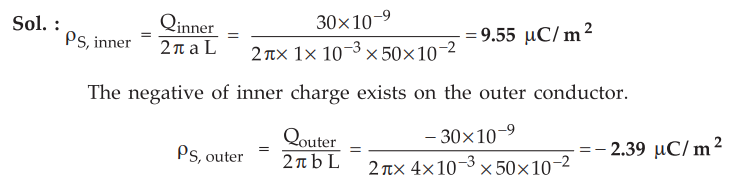
Examples for Practice

Ex. 3.7.6 The flux density  is in the free space :

a) Find  at r = 0.2 m.

b) Find the total electric flux leaving the sphere of r = 0.2 m.

c) Find the total charge within the sphere of r = 0.3 m.

Ex. 3.7.7 Three concentric spherical surfaces have radii r = 3, 5 and 7 cm respectively and have uniform charge densities of 200, - 50 and ρ×yC/m² respectively. Find.

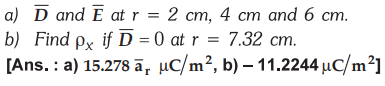
Ex. 3.7.8 If a sphere of radius ‘a’ has a charge density ρv = kr³ then find 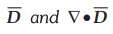 as a function of radius r and sketch the result. Assume k constant.

Ex. 3.7.9 Determine the flux crossing 1 mm by 1 mm area on cylindrical surface sheet of r = 20 m, ϕ = 55^o, z = 5 m, 

Review Questions

1. By means of Gauss's law, determine the electric field intensity at a point P at distant ’h’m from an infinite line of uniform charge ρL C/m

AU : Dec.-11, 14, Marks 8

2. State and prove Gauss’s law. State its applications.

AU : Dec.-03, 04, 05, May-05, 06, Marks 16

3. Evaluate D and E in all regions for a concentric spherical shell containing charge Q on it. Assume the charge distributions are infinite in extent.

AU : May-05, 06, 17,18, Dec.-02, Marks 13

4. State Gauss's law and give any two of its applications.

5. Apply Gauss’s law to an infinite sheet of charge.

AU : Dec.-11, Marks 16