Average Value

AVERAGE VALUE

Since the alternating quantity is a function of time, it becomes difficult to specify the quantity as so many amperes or volts. One of the ways to represent it is by an average value. Hence, we take the average of the instantaneous values of the wave (voltage or current), over one complete cycle.

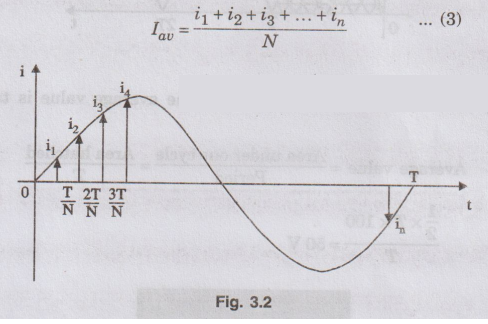
To explain about averaging a waveform, let us consider the time varying current shown in figure 3.2. Figure 3.2 shows only one complete cycle. If the time period is divided into a number of equal intervals, N, then the current at each interval of time is given by i₁, i₂, i₃ ... i_N and the average value is

Note we use small case letters (i, e or v) for instantaneous values and capitals (I, E or V) for constant values. Equation (3) gives better average value for larger values of N. A better way to find the average value is to integrate over a period and find the area under it and divide by T. Hence,

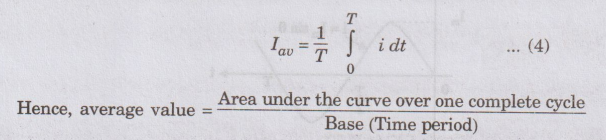
The average value of an alternating current is that value of steady direct current which transfers the same charge as the alternating current flowing for the same time.

For symmetrical waves, if the integration is done over a complete cycle, the average value over one full cycle becomes always zero (the positive half is similar to the negative half and so the two areas cancel each other). Hence for symmetrical waves, the average value is taken over half a cycle only. For unsymmetrical waves, the average value is taken over one complete cycle.

 

EXAMPLE 2: Find the average value of the triangular wave shown in figure.

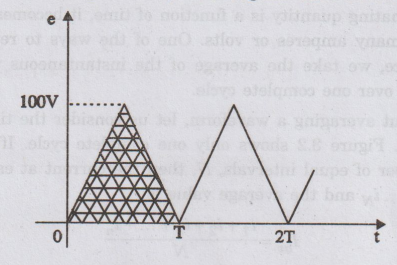
Solution:

This is an unsymmetrical wave and hence the average value is taken over one complete cycle.

Average value = 50 V

 

EXAMPLE 3: Find the average value of the sine wave shown in figure.

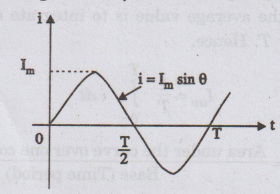
Solution:

This is a symmetrical wave. Hence, the average value is defined over half a cycle. (i.e., from 0 to T/ 2).

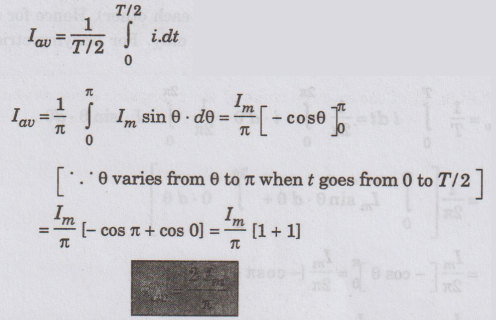
Note: The x-axis written in terms of time can also be written in terms of angles (in radians).

Period = T sec (or) 2π radians

Being a symmetrical wave, the average value is taken over л radians (T / 2 sec)

 

EXAMPLE 4: Find the average value of the (i) full rectified sine wave (figure (a)) (ii) half rectified sine wave. (figure (b)).

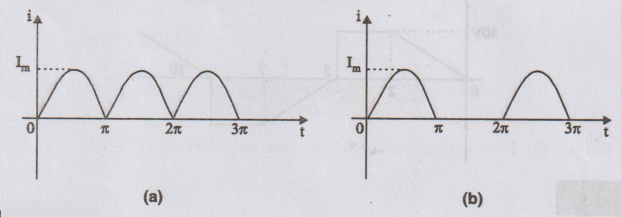
Solution:

 (ii) Period is T / 2 sec (2л radians)

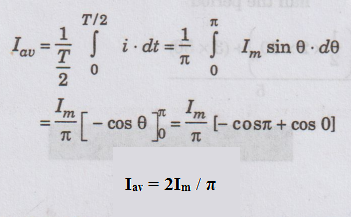
(ii) Period is T sec (2π radians) as the wave is unsymmetrical.

 

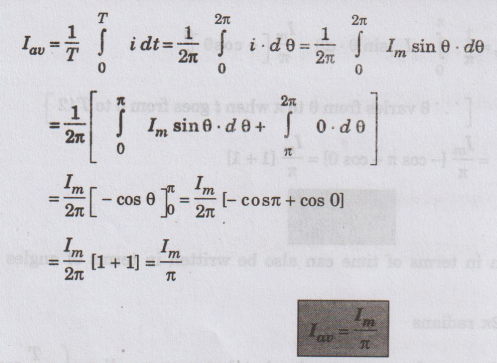
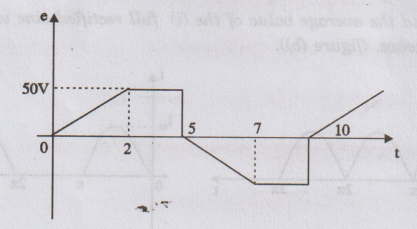
EXAMPLE 5 : Find the average value of the voltage waveform ahown in figure.

Solution:

Since this is a symmetrical wave, average value is defined over half cycle.

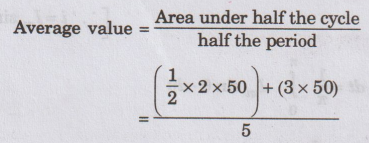
Average value = 40 Volts