Probability and complex function: Unit I: Probability and random variables
Axioms of probability
Theorem, Proof, Solved Example Problems
The probability of an event has been defined, we can collect the assumptions that we have made concerning probabilities into a set of axioms that the probabilities in any random experiment must satisfy.
AXIOMS OF PROBABILITY
The
probability of an event has been defined, we can collect the assumptions that
we have made concerning probabilities into a set of axioms that the
probabilities in any random experiment must satisfy.
The
axioms do not determine probabilities; the probabilities are assigned based on
our knowledge of the system under study. However, the axioms enable us to
easily calculate the probabilities of some events from knowledge of the
probabilities of other events.
Axioms
of probability
Probability
is a number that is assigned to each number of a collection of events from a
random experiment that satisfies the following properties : If S is the sample
space and E is any event in a random experiment,
Axiom
1 : 0 ≤ P (E) ≤ 1
Axiom
2 : P (S) = 1
Axiom
3: For any sequence of mutually exclusive events E1, E2, …
(i.e.,
events for which Ei Ej = ϕ when i ≠ j),
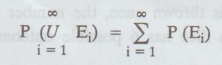
We
refer to P (E) as the probability of the event E nolaidmo er
Note
1:
Axiom 1 states that the probability that the outcome of the experiment is an
outcome in E is some number between 0 and 1.
Note
2:
Axiom 2 states that, with probability 1, the outcome will be a point in the
sample space S.
Note
3
: Axiom 3 states that for any sequence of mutually exclusive events the
probability of atleast one of these events occurring is just the sum of their
respective probabilities.
Theorem
1:
The
probability of an impossible event is zero (or) The null event has probability
0 (i.e.,) p (ϕ) = 0
Proof
:
If
we consider a sequence of events E1, E2, .. where E1
= S, Ei = ϕ
for
i > 1, then the events are mutually exclusive and as
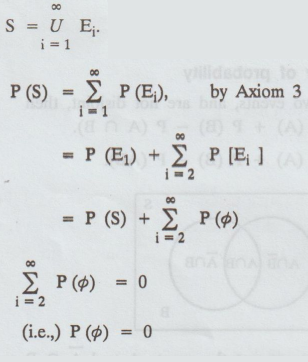
Theorem
2:
If
Ac is the complementary event of A, P(A) = 1 - P(A) ≤ 1.
Proof
:
A and Ac are mutually exclusive events, such that
A
∪ Ac = S
P(A
∪ Ac) = P(S)
=
1 by Axiom (ii)
P
(A) + P(Ac) = 1 by Axiom (iii)
P(Ac)
= 1 - P(A) since P (A) ≥ 0, it followes that P(Ac) ≤ 1.
Theorem
3:
If
B ⊂ A, P (B) ≤ P (A)
Proof
:
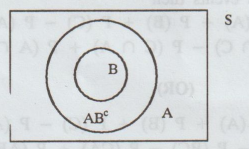
B
and A Bc are mutually exclusive events such that

Theorem
4 :Addition law of probability
If
A and B are any two events, and are not disjoint, then
P
(A ∪ B) = P (A) + P(B) - P
(A ∩ B).
(or)
P (A ∪ B) = P(A) + P(B)
Proof
:

Theorem
5
If
A, B and C are any three events then
P(A
∪ B ∪ C) = P(A) + P(B) +
P(C) - P (A ∩ B) - P (B ∩ C) - P (C ∩ A) + P(A ∩ B ∩ C)
(OR)
P
(A + B + C) = P (A) + P (B) + P(C) - P (AB) - P (BC) - P (CA) + P (ABC)
Proof:
Using the above result we have
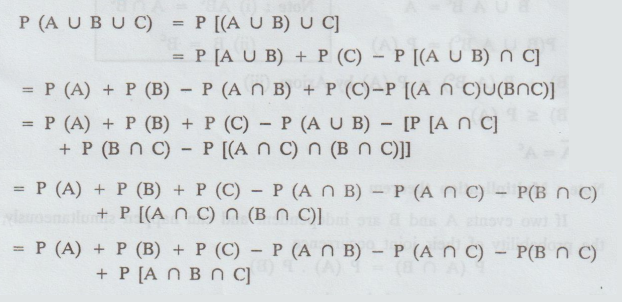
Theorem
6
If
A1, A2, … An are n mutually exclusive events
then the probability of the happening of one of them is
P
(A1 ∪
A2 ∪...
∪ An) = P (A1
+...+ An)
=
P (A1) + P(A2) + ... + P (An)
Proof:
Let N be the total number of mutually exclusive exhaustive and equally likely
cases of which m1 are favourable to A1, m2 are favourable
to A2 and so on.
Probability
of occurrence of A1 = P (A1) = m1 / N
Probability
of occurrence of A2 = P (A2) = m2 / N
…
… … … … … … … … … …
…
… … … … … … … … … …
Probability
of occurrence of An = P (An) = mn / N
The
events being mutually exclusive and equally likely, the number cases favourable
to the event A1 or A2 or … or An is mi +
m2 + … + mn
The
probability of occurrence of one of the events A1, A2,
... An is P
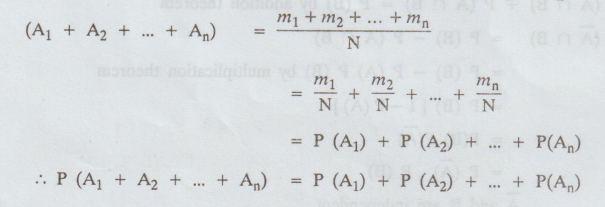
Note:
Multiplication theorem :
If
two events A and B are independent and can happen simultaneously, the
probability of their joint occurrence
P
(A ∩ B) = P(A) . P (B)
The
theorem can be extended to three or more events.
Theorem
7:
If
the events A and B are independent then

Sample
spaces having equally likely outcomes.
If
we assume that all outcomes of an experiment are equally likely to occur, then
the probability of any event E equals the proportion of outcomes in the sample
space that are contained in E.
P
(E) = number of points in E / number of points in S
♦
TYPE 1(a) P(A) = n (A) / n (S)
Example
1.1.1
Find
the probability that exactly one head appears in a single throw of a fair coin.
Solution
:
Formula
P (A) = n (A) / n (S)
Here
A be the event of getting exactly one head in a single throw of a fair coin.
S
- → Sample space = {H, T}
n
(S) = 2
n
(A) = 1
P
(A) = n (A) / n (S) = 1/2
Example
1.1.2
If
two dice are rolled, what is the probability that the sum of the upturned faces
will be equal to 7 ?
Solution
: The number of total outcomes is n (S) = 36
Let
A = {Sum of the upturned faces will equal 7}
=
{(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
n
(A) = 6
It
is assumed that all the 36 possible outcomes are equally likely.
P
(A) = n (A) / n (S) = 6 / 36 = 1 / 6
Example
1.1.3
From
a pack of 52 cards two cards are drawn the first being replaced before the
second is drawn. Find the probability that the first one is a diamond and
second is a king.
Solution:
Let A be an event of drawing a diamond.
P
(A) = n (A) / n (S) = 13/ 52 = 1 / 4
Let
B be an event of drawing a king.
P
(B) = n (B) / n (S) = 4 / 52 = 1/13
A
and B are independent events.
Hence
P (A ∩ B) = P(A).P (B) = (1/4) (1/13) = 1/52
Example
1.1.4
A
bag contains 5 white and 10 red balls. Three balls are taken out at random.
Find the probability that all the three balls drawn red.
Solution:
Total
number of balls = 15
S
= {Three balls are taken out of 15}
n
(S) = 15C3 = 15.14.13 / 1.2.3 = 455
Number
of red balls = 10
A
= {Three balls which are red}
n
(A) = 10 C3 = 10.9.8 / 1.2.3
= 120
P(A)
= n (A) / n (S) = 120 / 455 = 24 / 91
Example
1.1.5
If
3 balls are "randomly drawn" from a bowl containing 6 white and 5
black balls, what is the probability that one of the drawn balls is white and
the other two black ?
Solution
:
The
total number of balls = 11
Among
this 3 balls are randomly selected from the bowl.
Total
number of possible outcomes = n(S) = 11C3 = 11.10.9 / 1.2.3 = 165
The
number of favourable outcomes
(i.e.,
1 is white and the other two are black) = n(A) = 6C1 × 5C2
=
6 × 5.4/1.2 = 6 × 10 = 60
Hence
the required probability P(A) = n(A) / n(S) = 60/165 = 4/11
Example
1.1.6
A
lot of integrated circuit chips consists of 10 good, 4 with minor defects and 2
with major defects. Two chips are randomly chosen from the lot. What is the
probability that atleast one chip is good? [A.U M/J 2017]
Solution
:
P
(atleast one is good) = n (A) / n (S) = (10C1) (6C1) + 10C2
/ 16C2
=
(10) (6) + 45 / 120 = 60 + 45 / 120 = 105 / 120 = 7/8
Example
1.1.7
A
committee of 5 persons is to be selected randomly from a group of 5 men and 10
women. (a) Find the probability that the committee consists of 2 men and 3
women. (b) Find the probability that the committee consists of all women.
Solution:
(a)
The number of total outcomes is given by
n(S)
= 15C5
It
is assumed that "random selection" means that each of the outcomes is
equally likely.
Let
A = {The committee consists of 2 men and 3 women}
Then
n(A) = (5C2) (10C3)
P(A)
= n (A) / n (S) = (5C2) (10C3) / 15C5 = 400 /
1001 = 0.4
(b)
Let B = {the event that the committee consists of all women}
n(B)
= (5C0) (10C5)
P(B)
= n (B) / n (S) = (5C0) (10C5) / 15C5 = 36 /
429 = 0.084
Example
1.1.8
Four
persons are chosen at random from a group containing 3 men, 2 women and 4
children. Show that the chance that exactly two of them will be children is 10 /
21 [A.U N/D 2006]
Solution
:
Total
number of persons = 9
4
persons can be chosen out of 9 persons = 9C4 ways
=
9.8.7.6 / 1.2.3.4 = 126 ways.
The
number of ways of choosing 2 children out of 4 children = 4C2 ways
=
4.3/ 1.2 = 6 ways
The
remaining two persons can be choosen from 5 persons (3 men + 2 women)
= 5C2 ways
=
5.4 / 1.2 = 10 ways.
The
number of favourable case = 4C2 × 5C2 ways
=
6 × 10 ways
=
60 ways.
Required
probability = 60 / 126 = 10 / 21
Example
1.1.9
Four
persons are chosen at random from a group containing 3 men, 2 women and 4
children. Show that the chance that exactly two of them will be children is 10 /
21'
Solution
:
Total
number of persons = 9
4
persons can be chosen out of 9 persons = 9C4 ways
=
9.8.7.6 / 1.2.3.4 = 126 ways.
The
number of ways of choosing 2 children out of 4 children = 4C2 ways
=
4.3 / 1.2 = 6 ways
The
remaining two persons can be choosen from 5 persons (3 men + 2 women) = 5C2
ways
=
5.4 / 1.2 = 10 ways
The
number of favourable case = 4C2 ×
5C2 ways
=
6 × 10 ways
=
60 ways.
Required
probability = 60 / 126 = 10 / 21
Example
1.1.10
Two
dice are thrown together. Find the probability that (a) the total of the
numbers on the top face is 9 and (b) the top faces are same. [A.U. M/J 2006]
Solution
:
(a) Let A be the event which gives the sum of
the top numbers as 9.
Favourable
cases which gives the total as 9 are
(3,
6), (4, 5), (5, 4), (6, 3)
P(A)
= 4 / 36 = 1/9
(b)
Let B be the event which gives the top faces are same.
Favourable
cases are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6)
P(B)
= 6 / 36 = 1 / 6
Example
1.1.11
Out
of (2n + 1) tickets consecutively numbered three are drawn at random. Find the
probability that the numbers on them are in arithmetic progression. [A.U. M/J
2006]
Solution:
Out of (2n + 1) tickets, 3 tickets can be drawn in (2n+1) C3 ways.
total number of exhaustive cases
=
(2n + 1) (2n) (2n - 1) / 3! = n (4n2 - 1) / 3
To
find the favourable number of cases, we give all possibilities in which the
numbers on the drawn tickets are in A.P. with common difference d = 1, 2, 3, …,
n - 1, n (say)
If
d = 1, the possibilities are

If
d = n, then there is only one case as (1, n + 1, 2n + 1)
the
total number of favourable cases is + 5 + 3 + 1 which is an A.P. with common
difference 2.
Hence
favourable cases = n/2 [1 + (2n − 1)] = n2
=
The no. of favourable of cases / The no. of exhaustive cases
Thus
the required probability = n2 /
[n (4n2 - 1)/3] = 3n / 4n2 - 1
Type
1. (b) Mutually Exclusive events (disjoint)
P(A
∪ B) = P(A) + P(B)
(or) P(A + B) = P(A) + P(B)
Example
1.1.12
One
card is drawn from a pack of 52 cards. What is the probability that it is
either a king or a queen.
Solution:
A
= {an event that the card drawn is king}
P(A)
= n (A) / n (S) = 4/52 = 1/13
B
= {an event that the card drawn is queen}
P(B)
= n (B) / n (S) = 4/52 = 1/13
A
∪ B = {an event that the card
to be either a king or a queen}
P
( A ∪ B ) = P(A) + P(B) [ A
and B are mutually exclusive events]
=
1/13 + 1/13 = 2/13
Example
1.1.13
From
a group of 5 first year, 4 second year and 4 third year students, 3 students
are selected at random. Find the probability that they are first year or third
year students.
Solution
Total
number of students in the group = 13
Three
students are selected at random n (S) = 13 C3 = 13.12.11 / 1.2.3 =
286
A
→ The three students are from first year
i.e.,
n (A) = 5C3 = 5.4.3 / 1.2.3 = 10
P(A)
= n(A) / n(S) = 10 / 286
B
→ The three students are from third year
n
(B) = 4 C3 = 4
p
(B) = n(B) / n(S) = 4/286
Here
A and B are disjoint events since both cannot occur together.
P
(A ∪ B) = P(A) + P(B)
=
10 / 286 + 4 / 286 = 14 / 286 = 7 / 143
Example
1.1.14
A
bag contains 30 balls numbered from 1 to 30. One ball is drawn at random. Find
the probability that the number of the ball drawn will be a multiple of (a) 5
or 7 and (b) 3 or 7.
Solution:
Given:
n (S) = 30
Let
A = The probability of the number being multiple of 5.
P
(A) = p(5, 10, 15, 20, 25, 30) = 6 / 30
Let
B = The probability of the number being multiple of 7.
P
(B) = p(7, 14, 21, 28) = 4/30
Let
C = The probability of the number being multiple of 3.
P
(C) = p(3, 6, 9, 12, 15, 18, 21, 24, 27, 30) = 10 / 30
(a)
The events A and B are mutually exclusive the probability of the mix number
being a multiple of 5 or 7 will be
=
6/30 + 4/30 = 10/30
(b)
The events C and B are not mutually exclusive.
Here
p (C ∩ B) = p[21] = 1/30
p
(C ∪ B) = = p (C) + P(B) -p
(C ∩ B)
=
10 / 30 + 4 / 30 – 1 / 30 = 13 / 30
Example
1.1.15
What
is the probability of picking a card that was red or black?
Solution:
Let
A → The event of picking a red card.
B
→ The event of picking a black card.
P(A)
= 26 / 52 ;
p
(B) = 26 / 52
P(A
∪ B) = p (A) + p (B) = 26
/ 52 + 26 / 52
Since
A and B are mutually exclusive and exhaustive events.
Type
(1) (c) Not mutually exclusive, independent events
(i)
P (A ∪ B) = P(A) + P(B) – P (A
∩ B )
(ii)
P(A ∩ B) = P(A). P (B)
Example
1.1.16
A
coin is biased so that a head is twice as likely to occur as a tail. If the
coin is tossed 3 times, what is the probability of getting 2 tails and 1 head.
Solution: The sample space
Solution
:
The
sample space
S
= {HHH, HHT, HTH, THH, HTT, TTH, THT, TTT}
Since
a coin is biased and a head is twice as likely to occur as a tail,
P(H)
= 2/3 , and P(T) = 1 / 3
Let
A be the event of getting 2 tails and 1 head in the 3 tosses of the coin.
Then
A = {TTH, THT, HTT}
The
outcomes of the 3 tosses are independent,
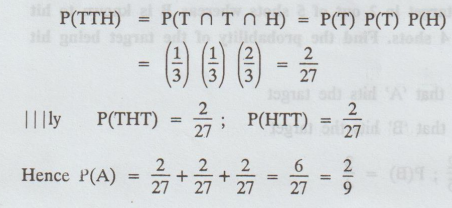
Example
1.1.17
A
can hit a target in 4 out of 5 shots and B can hit the target in 3 out of 4
shots. Find the probability that (i) the target being hit when both try. (ii)
the target being hit by exactly one person.
Solution:
Let
A, B the events
A
hit the target P(A) = 4/5
B
hit the target P(B) = 3/4
(i)
The events A and B are not mutually exclusive because both of them hit the
target.

Example
1.1.18
A
is known to hit the target in 2 out of 5 shots whereas B is known to hit the
target in 3 out of 4 shots. Find the probability of the target being hit when
they both try?
Sol.
: A → be the event that 'A' hits the target
B
→ be the event that 'B' hits the target
Given:
P(A) = 2/5 ; P(B) = ¾
To
find P (A ∪
B)
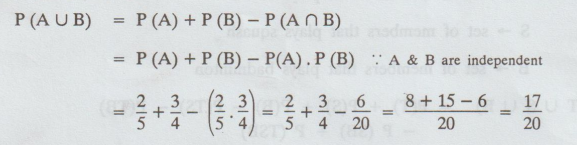
Example
1.1.19
One
card is drawn from a deck of 52 cards. What is the probability of the card
being either red or a king.
Solution:
Let
A = {an event that the card drawn is red}
B
= {an event that the card drawn is king}
A
∪ B = {an event that a card
to be either red or a king}
P
(A) = n (A) / n (S) = 26 / 52 = 1/2
P
(B) = n (B) / n (S) = 4 / 52 = 1/13
There
are two red coloured king cards.
So
P (A ∩ B) = 2/52 = 1/26
P
(A ∪ B) = P(A) + P(B) - P(A ∩
B)
[ A and B are not mutually exclusive]
=
1/2 + 1/13 – 1/26= 7/13
Example
1.1.20
A
total of 36 members of a club play tennis, 28 play squash, and 18 play
badminton. Furthermore, 22 of the members play both tennis and squash 12 play
both tennis and badminton, 9 play both squash and badminton, and 4 play all the
three sports. How many members of this club play atleast one of these sports ?
Solution
:
Let
N → the number of members of the club
C
→ any subset
P(C)
= number of members in C / N
Now
T
→ set of members that plays tennis
S
→ set of members that plays squash
B
→ set of members that plays badminton
P
(T ∪ S ∪ B) = P(T) + P(S) +
P(B) - P(TS) - P(TB) - P (SB) + P (TSB)
=
36 + 28 + 18 - 22 – 12 – 9 + 4 / N = 43 / N
Hence
we can conclude that 43 members play atleast one of the sports.
Example
1.1.21
If
A and B are events with P(A) = 3/8, P(B) = 1/2 and P(A ∩ B ) = 1/4,
find P(Ac ∩ Bc)
[A.U N/D 2006]
Solution:
We know that
P(A
∪ B) = P(A) + P(B) – P (A
∩ B)
=
3/8 + 1/2 – 1/4 = 3 + 4 – 2 / 8 = 5/8
P(Ac ∩ Bc) = 1 – P (A ∪ B)
=
1 – 5 / 8 = 3 / 8
Example
1.1.22
If
A and B are independent events with P(A) = 0.4 and P(B) = 0.5 find P(A ∪ B). [A.U. Dec,
96]
Solution:
Since
A and B are independent
P(A
∩
B) = P(A) P (B)
P(A
∪ B) = P(A) + P (B) – P(A ∩ B)
=
P(A) + P(B) - P(A) P(B)
=
0.4 + 0.5 – (0.4) (0.5)
=
0.9 - 0.2 = 0.7
Example
1.1.23
Let
events A and B be independent with P(A) = 0.5 and P(B) = 0.8. Find the
probability that neither of the events A nor B occurs. [A.U. May 2000]
Solution:
Since
A and B are independent
P(A
∩ B) = P(A) P(B)

Example
1.1.24
Event
A and B are such that P (A+B) = P(AB) = 1/4 AND 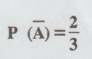 find P (B).
find P (B).
Solution
:

Example
1.1.25
If
P(A) = 0.4, P(B) = 0.7 and P(A ∩ B) = 0.3 find the probability that neither A
nor B occurs.
Solution
:
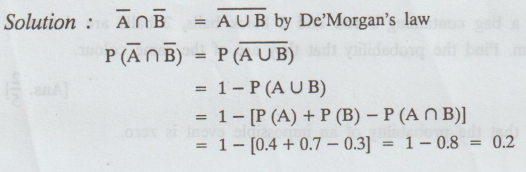
Example
1.1.26
If
you twice a flip a balanced coin, what is the probability of getting atleast
one head ?
Solution:
When
we flip a balanced coin, the sample space will be,
S
= {HH, HT, TH, TT}
P
(atleast one head) = 1-P (no head)
=
1 – 1/4 = 3/4
Example
1.1.27
Prove
that for any event A in 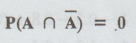
Solution
:
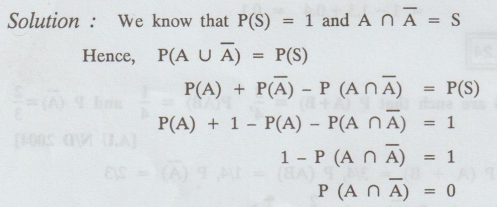
Probability and complex function: Unit I: Probability and random variables : Tag: : Theorem, Proof, Solved Example Problems - Axioms of probability
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
