Bearing and angles

BEARING AND ANGLES

Direction of Survey Line: The direction of a survey line can be established either (i) with relation to each other or (ii) with relation to any Meridian. The first will give the Angle between two lines. The second will give the Bearing of the line.

Bearing is the horizontal angle between the reference meridian and the survey line. It is measured in clock-wise direction.

Bearing of a Line is its direction relative to a given meridian.

Meridian: A Meridian is any direction such as True Meridian and Magnetic Meridian.

True Meridian is the line passing through the geographical North-South pole.

Magnetic Meridian is the direction shown by a magnetic needle (without being affected by magnetic substances), when the needle is suspended freely.

 

1. CLASSIFICATION OF BEARINGS

1. True Bearing: True Bearing of a survey line is the horizontal angle made by the line with the true North or geographical North. It is always measured in clock-wise direction. Range of measurement is from 0° to 360°.

2. Magnetic Bearing: Magnetic Bearing of a survey line is the horizontal angle which it makes with the magnetic North. It is always measured in clock-wise direction. Range of measurement is from 0° to 360°.

 

2. DESIGNATION OF BEARINGS OF SURVEY LINES

1. Whole Circle Bearing (W.C.B.)

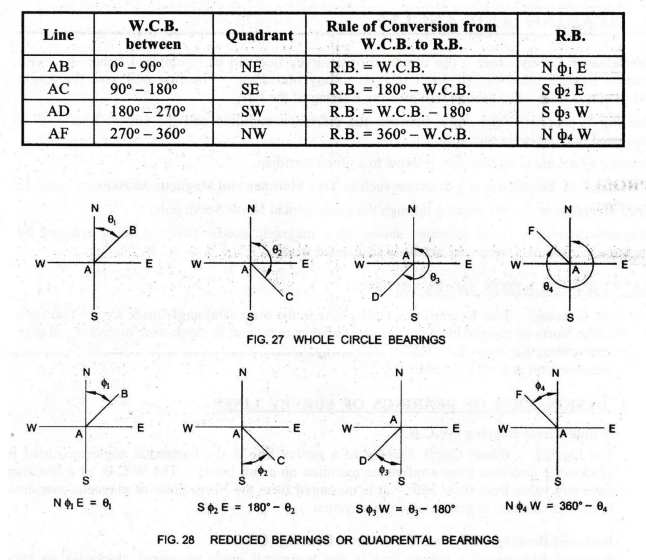
See Fig. 27. Whole Circle Bearing of a survey line is the horizontal angle measured in clock-wise direction from a reference meridian on a full circle. The W.C.B. of a line may have any value from 0° to 360°. It is measured from the North point of magnetic meridian. Prismatic compass is graduated on this system.

2. Reduced Bearing (R.B.) or Quadrantal Bearing (Q.B.)

Reduced Bearing of a survey line is the horizontal angle measured clockwise or anticlockwise from North end or South end of the reference meridian towards East or West whichever is nearer. Hence, to designate R.B. of a line, it is necessary to mention N or S to refer the meridian and E or W towards which the line is nearer. Thus, the plane round a station is divided into four quadrants, namely, NE, SE, SW and NW as shown in Fig. 28.

Note: R.B. of a line has value from 0° to 90° with prefix N or S and suffix E or W to indicate the quadrant in which the line lies. These bearings are noted by surveyor's compass.

 

3. CONVERSION OF WHOLE CIRCLE BEARING INTO REDUCED BEARING

The bearing of a line can be converted from Whole Circle Bearing (W.C.B.) system to Reduced Bearing (R.B.) system as explained in the Table and Figs. 27 and 28 below:

Note: When a survey line lies exactly along North, South, East or West and if

W.C.B. of the line = 0o,    then R.B. is N;

W.C.B. of the line = 90°,   then R.B. is E 90°;

W.C.B. of the line = 180°, then R.B. is S;

W.C.B. of the line = 270o,  then R.B. is W 90°.

 

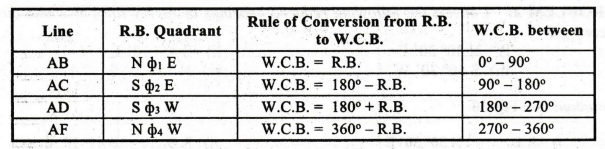
4. CONVERSION OF REDUCED BEARING INTO WHOLE CIRCLE BEARING

The bearing of a line can be easily converted from Reduced Bearing (R.B.) system to Whole Circle Bearing (W.C.B.) system as explained in the Table below:

 

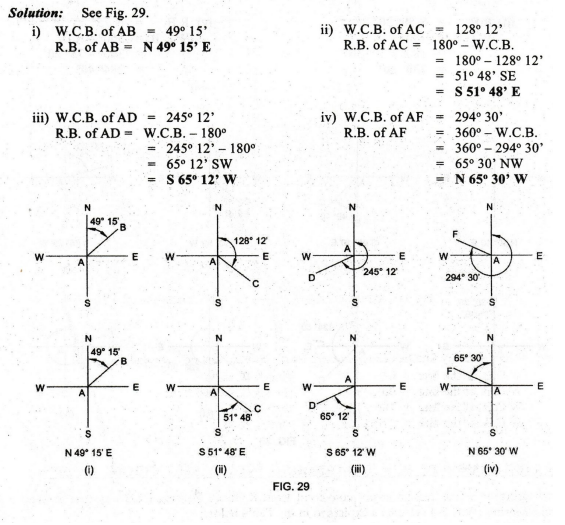
PROBLEM 1: Convert the following whole circle bearings of survey lines to reduced bearings:

i) AB = 49° 15'

ii) AC = 128° 12'

iii) AD = 245° 12'

iv) AF = 294° 30'

Solution: See Fig. 29.

 

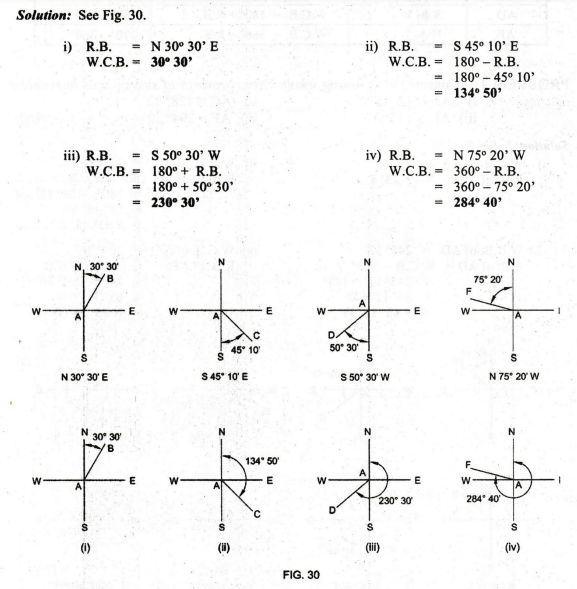
PROBLEM 2: Convert the following reduced bearings of survey lines to whole circle bearings:

i) N 30° 30' E

ii) S 45° 10' E

iii) S 50° 30'W

iv) N 75° 20' W

Solution: See Fig. 30.

 

5. FORE BEARING (F.B.) and BACK BEARING (B.B.)

In compass surveying, there are two bearings for each survey line, one measured from each end of the line. The two bearings are: Fore and Back Bearings. Both differ exactly by 180°.

Fore Bearing (F.B.): The bearing of a survey line taken in the direction of progress of survey or in the forward direction is known as Forward Bearing or Fore Bearing (F.B.).

See Fig. 31. F.B. is the angle measured from station A to station B in the direction in which the survey is conducted. Angle NAB = θ₁ = Fore Bearing.

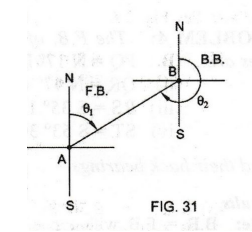
Back Bearing (B.B.): The bearing of a survey line taken in the direction opposite to the progress of survey or in the reverse direction is known as Backward Bearing or Back Bearing (B.B.).

See Fig. 31. Back bearing of survey line AB is the bearing taken from the next station B to its preceding station A from which the fore bearing was taken. Angle NBA = θ₂ = Back Bearing. Therefore, Fore Bearing ~ Back Bearing = 180^o.

Note: 1. In W.C.B. system, Back Bearing = F.B. 180° [+ve, if F.B. is less than 180° and -ve, if F.B. is greater than 180°).

2. In R.B. system, to convert F.B. into B.B. or vice versa, replace N by S, S by N, E by W and W by E without altering the numerical value of its bearing.

 

PROBLEM 3: The following are the observed fore bearings of the traverse lines. Find their back bearings. (UQ)

(i) AB = 24° 30'

(ii) BC = 114° 45'

(iii) CD = 213° 30'

(iv) DE = 356° 15'

Solution: See Fig. 32.

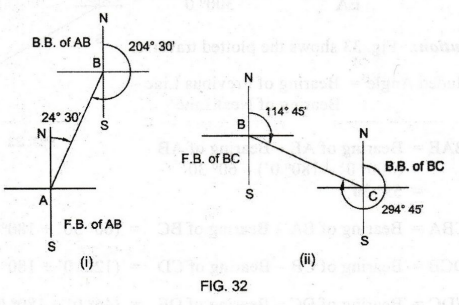
Rule : B.B = F.B. ± 180^o

(i) B.B. of AB

= 24^o 30^’ + 180^o

= 204^o 30^’

(ii) B.B. of BC

= 114^o 45^’ + 180⁰

= 294^o 45^’

(iii) B.B of CD = 213^o 30^’  - 180^o

= 30^o 30^’

(iv) B.B. of DE = 356^o 15^’  - 180^o

= 176^o 15^’

PROBLEM 4: The F.B. of the survey

lines are: (i) PQ = N 17° E.

(ii) QR = N 47° 40' W

(iii) RS = S 35° 15' E

(iv) ST =S 53° 30' W

Find their back bearings. (UQ).

Results

Rule: B.B. = F.B. with opposite letters of directions.

(i) B.B. of PQ = N 17° E = S 17° W

(ii) B.B. of OR = N 47° 40' W = S 47° 40' E

(iii) B.B. of RS = S 350 15'E = N 35° 15'W

(iv) B.B. of ST = S 53° 30' W = N 53° 30'E

PROBLEM 5: The following bearings were observed with a compass. Determine the interior angles.

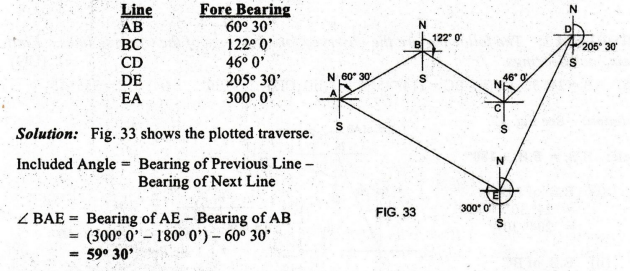
∠ CBA = Bearing of BA - Bearing of BC = (60° 30' + 180° 0') - 122° 0' = 118° 30'

∠DCB = Bearing of CB - Bearing of CD = (122° 0° +180° 0') - 46° 0' = 256° 0°

∠ EDC = Bearing of DC - Bearing of DE = (46° 0' + 180° 0') – 205° 30' = 20° 30°

∠ DEA = Bearing of ED - Bearing of EA = (205° 30' - 180° 0') - 300° 0' + 360° 0' = 85° 30'

Sum of Interior Angles = 540° 0'

Check: Sum of Interior Angles = (2n – 4) × 90^o = 540° 0'

 

PROBLEM 6: (Exercise) Compass readings at A, B, C, and D of a survey are given. Find the interior angles at A, B, C and D. Show that ABCD is a closed polygon. (UQ)

Bearing of AB = 140°, Bearing of BC = 210°, Bearing of CD = 290° and Bearing of DA = 550.

Results: ∠A = 95°, ∠B = 110°, ∠C = 100° and ∠D = 550.

1. Local Attraction

The compass needle is a magnetized one. It does not point to the magnetic North, if external magnetic influences are present. Such disturbance to compass needle due to the presence of magnetic field is termed as Local Attraction. .

The materials which influence magnetic action are the presence of magnetic steel structures, iron lamp posts, transmission towers, rails, etc. Even the commonly used iron materials such as screw driver, knife, etc., and the instruments used during the survey work such as chain, arrow, etc., may influence the correct bearing due to local attraction.

Local attraction is checked by finding the difference between the Fore Bearing and Back Bearing of a survey line. If the difference is not exactly equal to 180°, then it shows the presence of local attraction.