Behaviour of Synchronous Motor on Loading

Behaviour of Synchronous Motor on Loading

When a d.c. motor or an induction motor is loaded, the speed of the motor drops. This is because the load torque demand increases than the torque produced by the motor. Hence motor draws more current to produce more torque to satisfy the load but its speed reduces. In case of synchronous motor speed always remains constant equal to the synchronous speed, irrespective of load condition. It is interesting to study how synchronous motor reacts to changes in the load condition.

In a d.c. motor, armature develops an e.m.f. after motoring action starts which opposes supply voltage, called back e.m.f. E_b.

Hence if R_a is the armature resistance and V is the supply voltage, we have established the relation for the armature current I_a as,

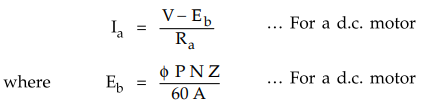
In case of synchronous motor also, once rotor starts rotating at synchronous speed, the stationary stator (armature) conductors cut the flux produced by rotor. The only difference is conductors are stationary and flux is rotating. Due to this there is an induced e.m.f. in the stator which according to Lenz's law opposes the supply voltage. This induced e.m.f. is called back e.m.f. in case of synchronous motor. It is denoted as Ebpb i.e. back e.m.f. per phase. This gets generated as the principle of alternator and hence alternating in nature and its magnitude can be calculated by the equation,

E_bph = 4.44 K_c K_d ϕ f T_ph 

or E_bph   oc ϕ

As speed is always synchronous, the frequency is constant and hence magnitude of such back e.m.f. can be controlled by changing the flux ϕ produced by the rotor.

Key Point So back e.mf. in case of synchronous motor depends on the excitation given to the field winding and not on the speed, as speed is always constant.

As stator construction is similar to the armature of a three phase alternator, the impedance of the stator is called synchronous impedance of synchronous motor consisting of R_a as the stator winding resistance and X_s as the synchronous reactance. All the values are generally expressed on per phase basis.

Z_s = R_a + j X_s Ω per phase

So similar to the d.c. motor, we can write voltage equation for a synchronous motor as,

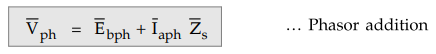
The difference is that this equation is vector equation as each quantity is alternating and has different phase. So addition is to be performed vectorially to obtain the result.

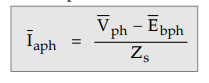
where V_ph is the supply voltage per phase. The magnitude of Ebph is adjusted almost equal to V_pb, on no load by controlling flux produced by rotor i.e. field winding.

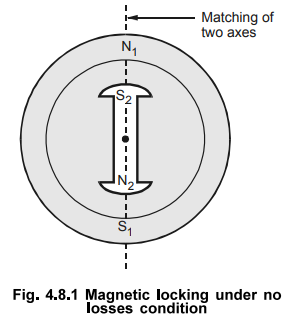
1. Ideal Condition on No Load

The ideal condition on no load can be assumed by neglecting various losses in the motor.

And V_ph = E_bph

Under this condition, the magnetic locking between stator and rotor is in such a way that the magnetic axes of both, coincide with each other as shown in the Fig. 4.8.1. As this is possible only under no losses condition, is said to be ideal in case of synchronous motor.

As magnitude of Ebph and Vpb is same and Ebph opposes Vph, the phasor diagram for this condition can be shown as in the Fig. 4.8.2.

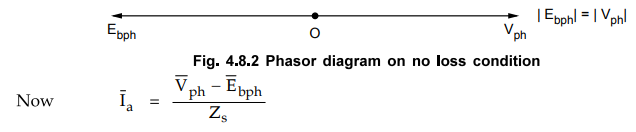
But the vector difference 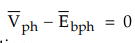  as seen from the phasor diagram. Hence I_a = 0 under no losses condition.

In practice this is impossible. Motor has to supply mechanical losses and iron losses alongwith small copper losses. To produce torque to overcome these losses, motor draws a current from the supply. Let us see how it can be explained in case of synchronous motor.

2. Synchronous Motor on No Load (With Losses)

We have seen that Ebph and Vpb are magnitudewise same, which is adjusted by controlling field current, in turn controlling the flux.

Now due to the various losses practically present on no load, the magnetic locking exists between stator and rotor but in such a way that there exists a small angle difference between the axes of two magnetic fields as shown in the Fig. 4.8.3.

So the rotor axis falls back with respect to stator axis by angle as shown in Fig. 4.8.3. This angle decides the amount of current required to produce the torque to supply various losses.

Hence this angle is called load angle, power angle, coupling angle, torque angle or angle of retardation and denoted as δ as mentioned earlier.

The magnetic locking still exists between the two and rotor rotates at synchronous speed alongwith rotating magnetic field maintaining angle difference between the axes of two field, as shown in the Fig. 4.8.3 (b). The flux lines between the two get stretched due to such retardation of rotor axis with respect to stator.

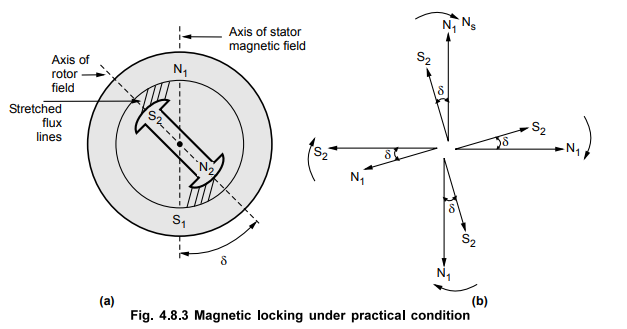
Now though | E_bph | = | V_ph |, E_bph will not be located in exact opposition with V_pb, but will get displaced from its initial position by angle 'δ' as shown in the Fig. 4.8.4.

Hence the vector difference between the two, Ebpb and Vpb is not zero but give rise to a phasor 'OB' as shown.

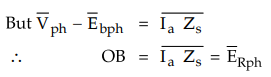
This is called resultant phasor denoted as  which is the product of armature current per phase and armature impedance per phase.

This resultant decides the amount of current I_aph to be drawn to produce the torque which meets the various losses present in the synchronous motor. Under no load condition, δ is very small and hence E_Rpb is also very small.

So current drawn by the motor is also very small on no load which is the case in all the various types of motors.

3. Synchronous Motor on Load

As the load on the synchronous motor increases, there is no change in its speed. But what gets affected is the load angle δ ’ i.e. the angle by which rotor axis retards with respect to stator axis.

Hence as load increases, 8 increases but speed remains synchronous.

As δ increases, though E_bpb and Vpb magnitudes are same, displacement of E_bpb from its ideal position increases. Hence the vector difference 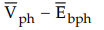increases. As synchronous impedance is constant, the magnitude of I_apb drawn by the motor increases as load increases. This current produces the necessary torque which satisfies the increased load demand. The magnetic locking still exists between the rotor and stator.

The phasor diagrams showing E_Rpb increases as load increases are shown in Fig. 4.8.5 (a) and (b).

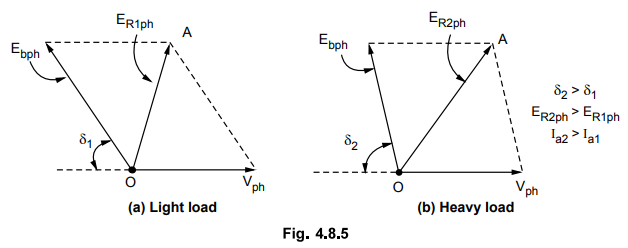
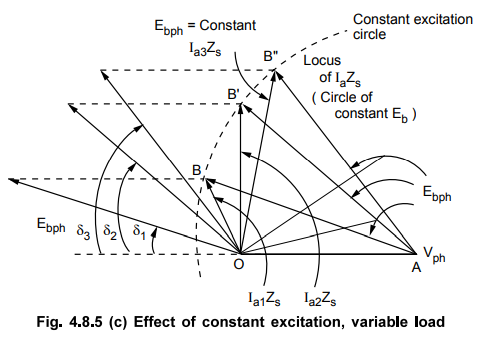
4. Constant Excitation Circle

As E_bph depends on flux, for constant excitation E_bph is constant. For constant excitation, if load is varied then δ keeps on changing, due to which 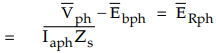 keeps on changing. The locus of extremities of

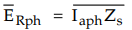 is a circle and as Z_s is constant, represents current locus for the synchronous motor under constant excitation and variable load conditions. As δ increases, Iaph Z_s increases and motor draws more current. As load decreases, δ decreases hence Iaph Z_s decreases and motor draws less current. Such a current locus is shown in the Fig. 4.8.5 (c).

So from the above discussion it is clear that on no load, current drawn by the motor is very small. This is because the stator and the rotor magnetic axes are almost matching each other i.e. load angle δ is very small. As load increases, rotor magnetic axis starts retarding with respect to stator axis i.e. load angle δ increases maintaining the magnetic locking condition. And hence in case of the synchronous motor load affects the angle 'δ' without affecting the speed. As δ increases, the magnitude of E_Rph increases which shows that motor draws more current from the supply. This satisfies the increased load torque demand.

The mechanical power developed by the synchronous motor is given by,

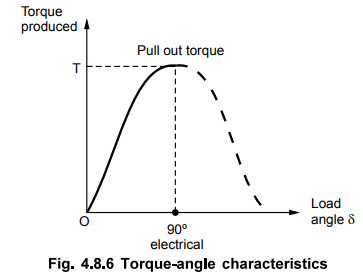
Key Point So torque produced in the synchronous motor depends on the load angle '8' for small values of 8 and to be precise depends on 'sin 8'. The load angle '8' is measured in degrees electrical.

As angle δ increases, the magnetic flux lines producing the force of attraction between the two get more and more stretched. This weakens the force maintaining the magnetic locking, though torque produced by the motor increases. As 8 reaches upto 90° electrical i.e. half a pole pitch, the stretched flux lines get broken and hence magnetic locking between the stator and rotor no longer exists. The motor comes out of synchronism. So torque produced at ’ δ ’ equal to 90° electrical is the maximum torque, a synchronous motor can produce, maintaining magnetic locking i.e. synchronism. Such a torque is called pull out torque. The relationship between torque produced and load angle 8 is shown in the Fig. 4.8.6.

5. Synchronous Motor Connected to Infinite Bus Bar

The synchronous motor connected to an infinite bus bar behaves similarly for the changes in the load at constant excitation. As the load increases, the load angle increases, current increases and power factor changes. The changes in the power factor depends on the excitation used for synchronous motor i.e. whether it is normally excited (Ebph = VpJ, over excited (E_bph > V_ph), or under excited (E_bph < V_ph)

Thus effect of change in load on synchronous motor connected to an infinite bus bar can be summarized as,

1. Irrespective of excitation, as load increases, the load angle δ and armature current I_a increases. 

2. When the motor is normally excited (E_bph = V_ph), then as load increases, the change in current is more significant than the change in power factor. The power factor tends to become more and more lagging as the load increases.

3. When the motor is over excited or under excited, the power factor changes are more significant than the changes in the current as load changes.

4. When the motor is over excited or under excited, the power factor tends to approach to unity as the load increases.

6. Torques in Synchronous Motor

The different torques in synchronous motor are,

1) Starting torque : This is the torque developed by the synchronous motor at start when rated voltage is applied to the stator. It is also called breakaway torque. It is necessary to overcome friction and inertia.

2) Running torque : It is the torque developed by the motor under running conditions. It is decided by the output rating of the motor and speed of the driven machine.

3) Pull in torque : Initially synchronous motor is rotated at a speed slightly less than the synchronous speed. When speed is near to synchronous, excitation is switched on and motor gets pulled into synchronism and starts rotating at the synchronous speed. The amount of torque developed by the motor at the time of pulling into synchronism is called pull in torque.

4) Pull out torque : When the synchronous motor is loaded, the rotor falls back with respect to stator by an angle called load angle δ. As δ increases, magnetic locking between stator and rotor decreases. At 8 = 90°, the torque developed is maximum by the motor and magnetic locking is very weak. Any further increase in the load pulls motor out of synchronism and motor stops. Thus the maximum torque developed by the synchronous motor without pulling out of synchronism is called pull out torque.

Review Questions

1. Explain the effect of variable load with constant excitation on synchronous motor. AU : May-13, Marks 6

2. Draw the torque-angle characteristics of synchronous motor and define pull-in and pull-out torque.

3. Define the various torques associated with the synchronous motor.

4. Describe in detail about the effect of load change on load angle and power factor of a three phase synchronous motor operating on infinite bus bar and constant ey

5. Explain the constant excitation circles for synchronous motor.