Digital Logic Circuits: Unit I: (a) Number Systems
Binary Arithmetic
Operation Table, Example Problems | Addition, Subtraction, Multiplication, Division
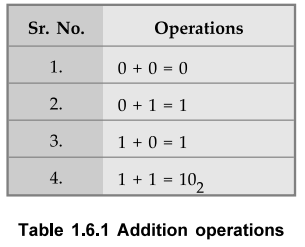
• The addition consists of four possible elementary operations, as shown in Table 1.6.1.
Binary Arithmetic
1. Binary Addition
•
The addition consists of four possible elementary operations, as shown in Table
1.6.1.
•
The first three operations produce a sum whose length is one digit, but when
the last operation is performed stun is two digits.
•
The higher significant bit of this result is called a carry significant bit is
called sum.
•
Such a operation is known as half addition.
•
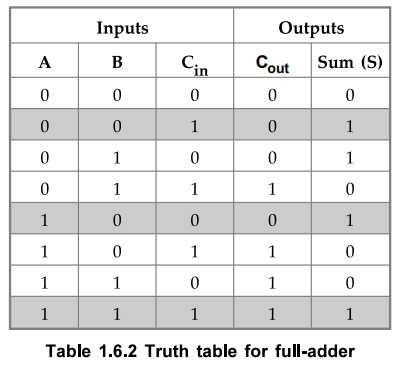
The operation which performs addition of three bits (two significant bits and a
previous carry) is called a full addition.
•
The Table 1.6.2 shows the truth table for full addition.
Addition
Method
1.
Add bits column-wise starting from LSB with carry if any.
2.
Put the sum at the bottom of the same column.
3.
Put the carry, if any, on the top of next column.
Ex.
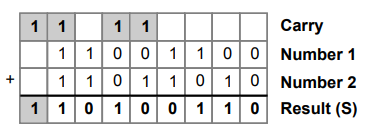
1.6.1 Perform addition of(11001100)2 and (11011010)2
Sol.
: In the above example, we have seen the addition
of two unsigned binary numbers. In case of the signed numbers, we have to
consider the sign of the number and we may require sign extension to avoid
possible overflow.
Ex. 1.6.2 Add (28)10 and (15)10 by converting them into binary.
Sol.
: Using decimal to binary conversion technique
discussed in section 1.3.8 we have,
(28)10
= (011100)2 and (15)10 = (01111)2

2. Binary Subtraction
•
The subtraction consists of four possible elementary operations, as shown in
Table 1.6.3.

•
In all operations, each subtrahend bit is subtracted from the minuend bit. In
case of second operation the minuend bit is smaller than the subtrahend bit,
hence 1 is borrowed.
Subtraction
Method
1.
Subtract bits column-wise starting from LSB with borrow if any.
2.
Put the difference at the bottom of the same column.
3.
Take the borrow, if required from the next column.
Ex.
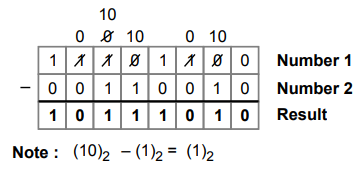
1.6.3 Perform (11101100)2 - (00110010)2.
Sol.
:
•
However, the subtraction technique we have just seen is difficult to implement
in a computer. Thus, computer uses 2's complement representation to implement
negative number.
3. Binary Subtraction using 1's Complement Method
•
In a l's complement subtraction, negative number is represented in the l's
complement form and actual addition is performed to get the desired result.
•
For example, operation A - B is performed using following steps :
1.
Take l's complement of B.
2.
Result ← A + l's complement of B.
3.
If carry is generated then the result is positive and in the true form. Add
carry to the result to get the final result.
4.
If carry is not generated then the result is negative and in the l's complement
form.
Ex.
1.6.4 Perform subtraction using l's complement (11010)2 - (10000)
2
AU
: CSE : Dec.-09, Marks 2
Sol.
:
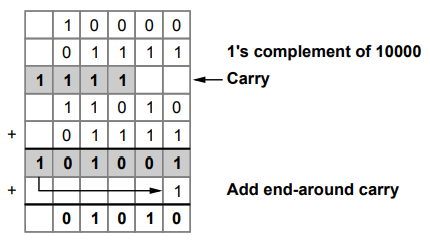
Ex.
1.6.5 Perform (15)10 -(28)w using l’s complement representation.
Sol.
:

4. Binary Subtraction using 2's Complement Method
•
In a 2's complement subtraction, negative number is represented in the 2's
complement form and actual addition is performed to get the desired result.
•
For example, operation A - B is performed using following steps :
1.
Take 2's complement of B.
2.
Result ← A + 2's complement of B.
3.
If carry is generated then the result is positive and in the true form. In this
case, carry is ignored.
4. If carry is not generated then the result is negative and in the 2's complement form.
Ex.
1.6.6 Perform (147 – 89) using 2’s complement binary arithmetic.
Sol.
:
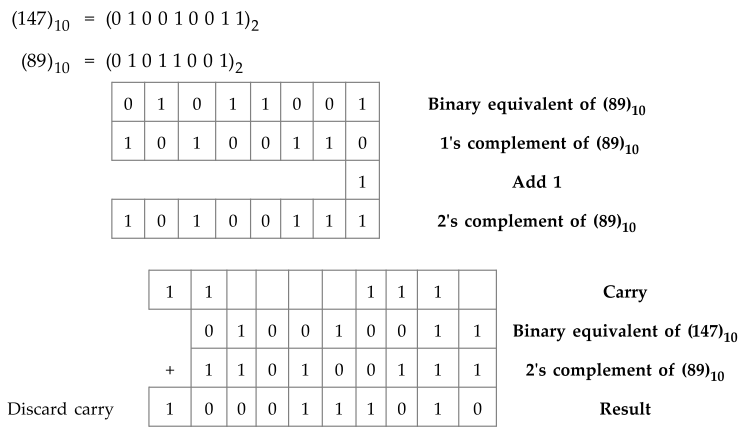
Ex.
1.6.7 Using 2's complement perform (42)10 - (68)10.
Sol.
:
Step
1 :
Convert (42)10 to its binary equivalent.
(42)10
= (101010)2
Step
2 :
Convert 6810 to its binary equivalent.
(68)
10 = (1000100)2
Step
3 :
Find 2's complement of 68.
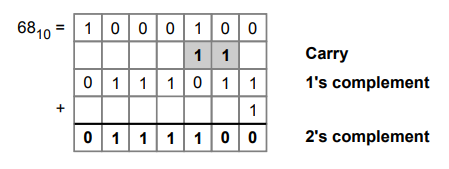
Step
4 :
Add (1 0 1 0 1 0)2 and (0 1 1 1 1 0 0) 2 Since we have
subtracted larger number from smaller number result is negative and hence it is
necessary to take 2's complement of this result.

Step
5 :
Find 2's complement of (1100110)2. Since we have taken 2's complement result is
(-26)10.
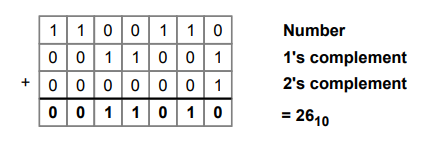
5. Binary Multiplication
The
multiplication process for binary numbers is similar to the decimal numbers.
•
Actually binary multiplication is simple than decimal multiplication since it
involves only 1s and Os.
The
Table 1.6.4 shows rules for binary multiplication.

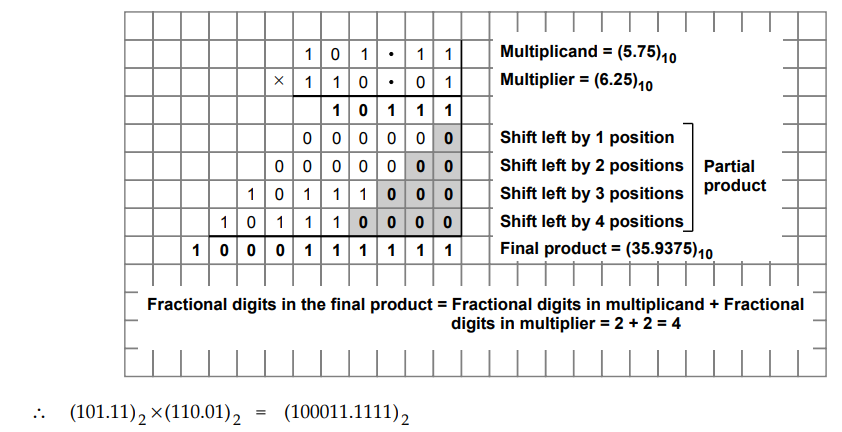
Ex. 1.6.8 Multiply (101.11)2 and (110.01) 2 using binary multiplication method.
Sol
. :
6. Binary Division
•
The division process for binary numbers is similar to the decimal numbers.
•
In binary division, division by 0 has no meaning.
Table
1.6.5 shows the rules for binary division.

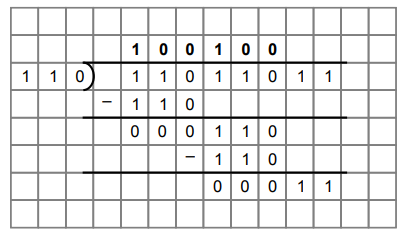
Ex.
1.6.9 Divide U0110U2
by 1102.
Sol.
:
Review Questions
1. Illustrate the rules for binary addition and subtraction
using 2's complement arithmetic. Give examples.
AU : CSE : May-06, Harks 8
2. State the rules for binary multiplication.
3. State the rules for binary division.
Digital Logic Circuits: Unit I: (a) Number Systems : Tag: : Operation Table, Example Problems | Addition, Subtraction, Multiplication, Division - Binary Arithmetic
Related Topics
Related Subjects
Digital Logic Circuits
EE3302 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
