Binary Codes

Binary Codes

AU : Dec.-02,03,09,15, May-03,07,12

• When numbers, alphabets or words are represented by a specific group of symbols, we can say that they are encoded.

• The group of symbols used to encode them are called codes. The digital data is represented, stored and transmitted as groups of binary digits (bits).

• The group of bits, also known as binary code, represent both numbers and letters of the alphabets as well as many special characters and control functions. They are classified as numeric or alphanumeric.

• Numeric codes are used to represent numbers.

• Alphanumeric codes are used to represent characters : alphabetic letters and numerals.

1. Classification of Binary Codes

• The Fig. 1.7.1 shos the classification of codes.

• The codes are broadly classified as

1. Weighted codes

2. Non-weighted codes

3. Reflective codes

4. Sequential codes

5. Alphanumeric codes

6. Error detecting and correcting codes.

Weighted codes

• In weighted codes, each digit position of the number represents a specific weight.

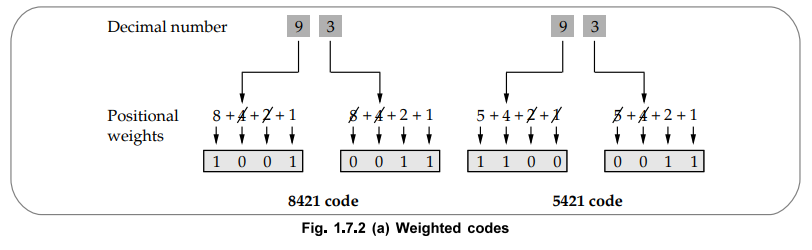
• For example, in decimal code, if number is 567 then weight of 5 is 100, weight of 6 is 10 and weight of 7 is 1.

• In weighted binary code each bit has a weight 8, 4, 2 or 1 and each decimal digit is represented by a group of four bits, as shown in the Fig. 1.7.2 (a).

Non-weighted codes

• Non-weighted codes are not assigned with any weight to each digit position, i.e., each digit position within the number is not assigned fixed value.

• Excess-3 and gray codes are the non-weighted codes.

Reflective codes

• A code is said to be reflective when the code for 9 is the complement for 0, the code for 8 is complement for 1, 7 for 2, 6 for 3 and 5 for 4. This is illustrated in Fig. 1.7.2 (b).

• Like 2421, codes 5211 and excess-3 are also reflective. The 8421 code is not reflective.

• Reflectivity is desirable in a code when the nine's complement must be found, such as in nine's complement subtraction.

Sequential codes

• In sequential codes each succeeding code is one binary number greater than its preceding code.

• This greatly aids mathematical manipulation of data.

• The 8421 and excess-3 are sequential, whereas the 2421 and 5211 codes are not.

Alphanumeric codes

• The codes which consists of both numbers and alphabetic characters are called alphanumeric codes.

• Most of these codes, however, also represent symbols and various instructions necessary for conveying intelligible information.

• The most commonly used alphanumeric codes are : ASCII (American Standard Code for Information Interchange), EBCDIC (Extended Binary Coded Decimal Interchange Code) and Hollerith code.

Error detecting and correcting codes

• When the digital information in the binary form is transmitted from one circuit or system to another circuit or system an error may occur. This means a signal corresponding to 0 may change to 1 or vice versa due to presence of noise.

• To maintain the data integrity between transmitter and receiver, extra bit or more than one bit are added in the data.

• These extra bits allow the detection and sometimes correction of error in the data. 

• The data along with the extra bit/bits forms the code. Codes which allow only error detection are called error detecting codes and codes which allow error detection and correction are called error detecting and correcting codes.

2. BCD (Binary Coded Decimal) Codes

• BCD is an abbreviation for binary coded decimal.

• BCD is a numeric code in which each digit of a decimal number is represented by a separate group of 4-bits. The most common BCD code is 8-4-2-1 BCD.

• It is called 8-4-2-1 BCD because the weights associated with 4 bits are 8-4-2-1 from left to right. This means that, bit-3 has weight 8, bit-2 has weight 4 bit-1 has weight 2 and bit-0 has weight 1.

• The Table 1.7.1 shows the 4-bit 8-4-2-1 BCD code used to represent a single decimal digit.

• In multidigit coding, each decimal digit is individually coded with 8-4-2-1 BCD code, as shown in the Fig. 1.7.3. Total 8-bits are required to encode 5810 in 8-4-2-1 BCD.

Advantage

1. Easy to convert between it and decimal.

Disadvantages

1. Since it requires more binary digits to represent multi-digit number than binary number system. It is less efficient. For example, to represent the same number (58) in binary : 1110102, we require only 6 digits.

2. Arithmetic operations are more complex.

a. BCD Addition

• The addition of two BCD numbers can be best understood by considering the three cases that occur when two BCD digits are added.

Case 1 : Sum equals 9 or less with carry 0

• Let us consider additions of 3 and 6 in BCD.

• The addition is carried out as in normal binary addition and the sums are 10 0 1 and 0 111 which are valid BCD codes. 

Case 2: Sum greater than 9 with carry 0

• Let us consider addition of 6 and 8 in BCD.

The sum 1 1 10 is an invalid BCD number. This has occurred because the sum of the two digits exceeds 9. Whenever this occurs the sum has to be corrected by the addition of six (0110) in the invalid BCD number, as shown.

• After addition of 6 carry is produced into the second decimal position.

Case 3 : Sum equals 9 or less with carry 1

• Let us consider addition of 8 and 9 in BCD.

• In this case, result (0001 0001) is valid BCD number, but it is incorrect. To get the correct BCD result correction factor of 6 has to be added to the least significant digit sum, as shown.

Procedure of BCD Addition

• Going through these three cases of BCD addition we can summarize the BCD addition procedure as follows :

1. Add two BCD numbers using ordinary binary addition.

2. If four-bit sum is equal to or less than 9, no correction is needed. The sum is in proper BCD form.

3. If the four-bit sum is greater than 9 or if a carry is generated from the four-bit sum, the sum is invalid.

4. To correct the invalid sum, add 6 (0110₂) to the four-bit sum. If a carry results from this addition, add it to the next higher-order BCD digit.

Ex. 1.7.1 Perform the code conversion :    (137)₁₀ = (?) NBCD

Sol. : NBCD = 8421 BCD

(137)₁₀ = (0001 0011 0111)_NBCD 

Ex. 1.7.2 Perform each of the following decimal additions in 8-4-2-1 BCD.

Sol. :

b. BCD Subtraction using 9's Complement Method

• Subtraction of BCD numbers can be performed by representing negative numbers in the 9's complement form.

• The 9's complement of a decimal number is found by subtracting each digit in the number from 9.

• The 9's complement of each of the decimal digits is as follows :

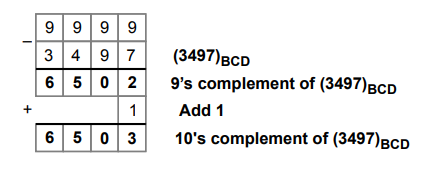
Ex. 1.7.3 Find the 9's complement of(3497)_BCD.

Sol. :

Step 1 : Find the 9's complement of a negative number.

Step 2 : Add two numbers using BCD addition (Minuend + 9's complement of subtrahend).

Step 3 : If carry is not generated result is negative and find the 9's complement of the result, otherwise result is positive and add carry to the result.

Ex. 1.7.4 Perform (46)₁₀ - (22) ₁₀ in BCD using 9's complement.

Sol. :

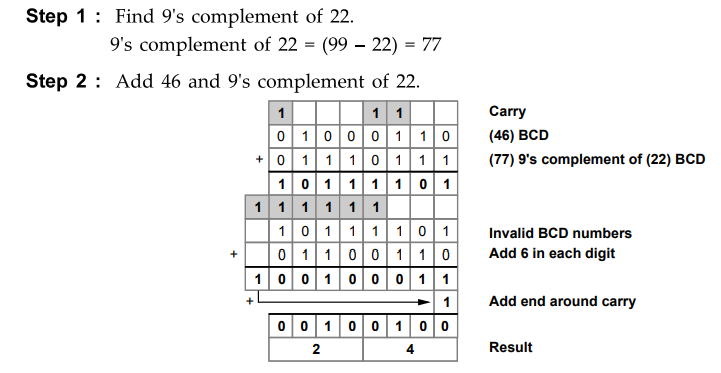
Since there is a carry the result is positive and true.

(46)_BCD – (22) _BCD = (24) _BCD

Ex. 1.7.5 Perform (24)₁₀ -(56)₁₀ in BCD using 9’s complement.

Sol. :

Step 1 : Find 9's complement of 56 9's complement of 56 = 99 - 56 = 43

Step 2 : Add (24)10 and 9's complement of 56 Since carry is 0 the answer is negative.

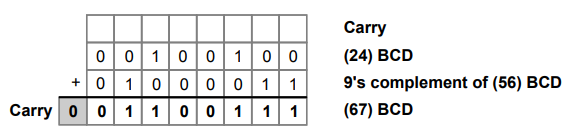
Step 3 : Take 9's complement of answer

9's complement of 67 = 99 - 67 = 32

(24)₁₀ - (56)₁₀ = (- 32)₁₀

c. BCD Subtraction using 10's Complement Method

• Subtraction of BCD numbers can also be performed by representing negative numbers in the 10's complement form.

• The 10's complement of a decimal number is equal to the 9's complement plus 1.

Ex. 1.7.6 Find the 10's complement vf(3497) _BCD.

Sol.

Steps for subtraction of BCD numbers using 10's complement method

Step 1 : Find the 10's complement of a negative number.

Step 2 : Add two numbers using BCD addition (Minuend + 10's complement of subtrahend).

Step 3 : If carry is not generated result is negative and find the 10's complement of the result, otherwise result is positive and discard carry.

Ex. 1.7.7 Perform (46)₁₀ - (22)₁₀ in BCD using 10's complement.

Sol. :

Step 1 : Find 10's complement of 22.

10's complement of 22 = 9's complement of 22 + 1 = (99 - 22) + 1 = 78

Step 2 : Add 46 and 10's complement of 22.

Since there is a carry the result is positive and true.

(46) _BCD - (22) _BCD = (24) _BCD

Ex. 1.7.8 Perform (24)₁₀ - (56)₁₀ in BCD using 10’s complement.

Sol. :

Step 1 : Find 10's complement of 56.

10's complement of 56 = 9's complement of 56 + 1

= (99 - 56) + 1 = 44

Step 2 : Add (24)10 and 10's complement of 56.

Since carry is 0 the answer is negative.

Step 3 : Take 10's complement of answer.

10's complement of 68 = 9's complement of 68 + 1

= (99 - 68) + 1 = 32

(24) ₁₀ - (56) ₁₀  =   - (32) ₁₀

Ex. 1.7.9 Perform 9's and 20's complement subtraction between 18 and - 24.

Sol. : Using 9's complement representation.

Step 1 : Find 9's complement of 24

9's complement of 24 = 99 - 24 = 75

Step 2 : Add 18 and 9's complement of 24

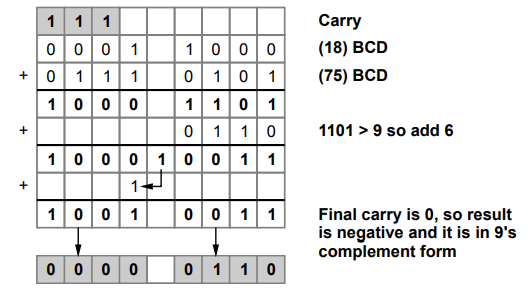
Using 10’s complement representation

Step 1 : Find 10’s complement of 24

10’s complement of 24 = 9’s complement of 24 + 1

= 75 + 1 = 76

Step 2 : Add 18 and 10’s complement of 24

(18) – (24) = -6

3. Other 4 – bit BCD Codes

a. 2-4-2-1 Codes

• The 2-4-2-1 BCD is another self complementing code or reflective code.

• Its 4-bit code groups are weighted. In this case, the weights are 2-4-2-1, meaning that bit 1 and bit 3 have the same weight (2). It is sometimes referred to as 2*- 4-2-1 code, where the asterisk simply distinguishes one position with weight 2 from the other.

• Since two positions have the same weight, there are two possible bit patterns that could be used to represent some decimal digits, but only one of those patterns is actually assigned.

• Table 1.7.3 shows the code assignments for 2-4-2-1 code.

• The Table 1.7.4 shows the reflective or self complementing property of 2421 code.

• It shows that, in 2421 code, code for 9 is complement of code 0, code for 8 is complement of code 1 and so on.

• There are various other weighted 4-bit BCD codes, each developed to have certain properties useful for special applications.

• Table 1.7.5 shows these codes, identified by the weights assigned to their bit positions.

• The  code is somewhat different than the other codes. When 1 occurs in either of the two rightmost positions means that the weight of that position is subtracted, rather than added, to determine the decimal value.

Ex. 1.7.10 Represent (7)10 using all the weighted 4-bit BCD cods listed in the Table 1.7.5.

Sol. :

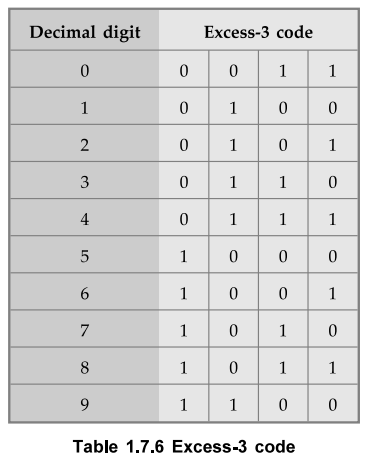
• The excess-3 code can be derived from the natural BCD code by adding 3 to each coded number.

• For example, decimal 12 can be represented in BCD as 0001 0010. Now adding 3 to each digit we get Excess-3 code as 0100 0101 (12 in decimal). It is a non-weighted code.

• Table 1.7.6 shows excess-3 codes to represent single decimal digit. It is sequential code because we get any code word by adding binary 1 to its previous code word as shown in the Table 1.7.6.

• In excess-3 code we get 9's complement of a number by just complementing each bit. Due to this excess-3 code is called self-complementing code or reflective code. 

Ex. 1.7.11 Find the excess-3 code and its 9's complement for following decimal numbers, a) 592 b) 403

Sol. :

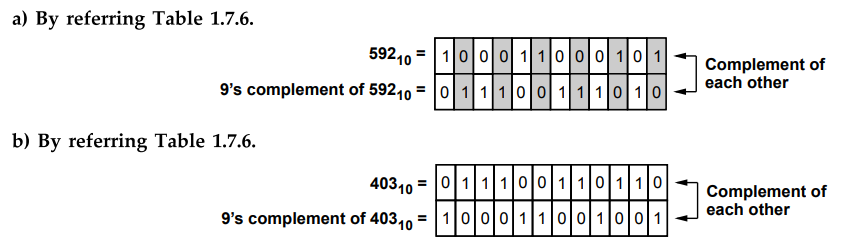
a. Excess-3 Addition

To perform excess-3 addition we have to

• Add two excess-3 numbers using binary addition.

• If carry = 1 → add 3 (0 0 11)₂ to the sum of two digits.

= 0 →subtract 3 (0 0 11)₂ from the sum.

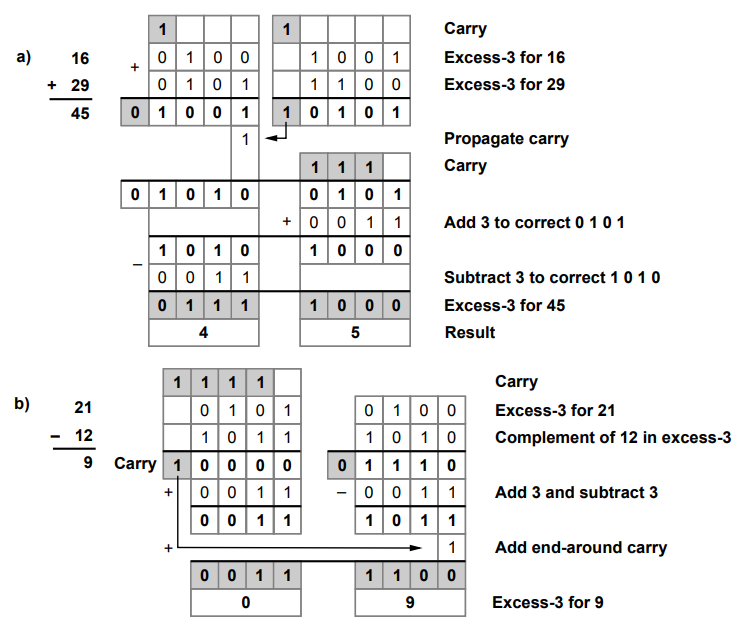
Ex. 1.7.12 Perform the excess-3 addition of a) 8,6 b) 1,2

Sol. :

b. Excess-3 Subtraction

• To perform excess-3 subtraction we have to

* Complement the subtrahend.

* Add complemented subtrahend to minuend.

* If carry = 1 Result is positive. Add 3 (0 0 1 1)₂ and end-around carry.

If carry = 0 Result is negative. Subtract 3 (0 0 11) ₂.

Ex. 1.7.13 Perform the excess-3 subtraction of a) 8 - 5, b) 5 - 8.

Sol. :

Note : In excess-3, 9's complement and complement of any number is same. So this excess-3 subtraction method is also known as excess-3 subtraction using 9's complement.

Ex. 1.7.14 Perform each of the following operations in excess -3 code.

 Sol. :

Examples for Practice 

Ex. 1.7.15 Represent decimal number 327 in Excess-3 code.

[Ans.: 0110 0101 1010]

Ex. 1.7.16 What is Excess-3 code of binary numbers : 0010 B, 0110 B and 0111 B ?

[Ans.: 0101,1001,1010]

Ex. 1.7.17 Represent the decimal number a) 396 and b) 4096 in Excess-3 code.

[Ans.: a) 0110 1100 1001 b) 0111001111001001]

5. Gray Code

• Gray code is a non-weighted code and is a special case of unit-distance code.

• In unit-distance code, bit patterns for two consecutive numbers differ in only one bit position. These codes are also called cyclic codes.

• The Table 1.7.7 shows the bit patterns assigned for gray code from decimal 0 to decimal 15.

• As shown in the Table 1.7.7 for gray code any two adjacent code groups differ only in one bit position.

• Reflective Property : The gray code is also called reflected code. Notice that the two least significant bits for 410 through 710 are the mirror images of those for Oo through 310. Similarly, the three least significant bits for 810 through 1510 are the mirror images of those for 0₁₀ through 7₁₀.

• In general, the n least significant bits for 2n through 2ⁿ + 1 - 1 are the mirror images of those for 0 through 2ⁿ - 1.

a. Application of Gray Code

• Let us consider an application where 3-bit binary code is provided to indicate position of the rotating disk with the help of brushes.

• When brushes are on the black portion, they output a 1. When on the white portion, they output a 0.

• Now consider what happens when the brushes are on the 111 sector and almost ready to enter the 000 sector.

• If one brush is slightly ahead of the other, say the 3rd brush, then the position is indicated by a Oil instead of a 111 or 000. This results, a 180° error in the disk position.

• Since it is physically impossible to have all the brushes precisely aligned, some error will always be present at the edges of the sectors.

• If we use gray code to represent disk position then error due to improper brush alignment can be reduced. This is because the gray code assures that only one bit will change each time the decimal number is incremented.

• So in 3-bit code, error may occur due to one bit position. Other two bits positions of two adjacent sectors are always same and hence there is no possibility of error.

• Therefore in 3-bit code probability of error is reduced upto 66 %. In case of 4-bit code it is reduced upto 75 %. This is an important advantage of gray code.

b. Gray to Binary Conversion

Steps for gray to binary code conversion

1. The Most Significant Bit (MSB) of the binary number is the same as the most significant bit (MSB) of the gray code number. So Write down MSB as it is.

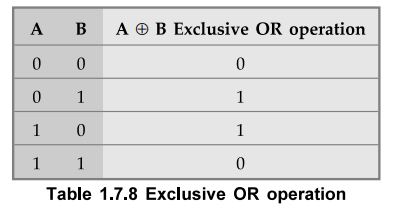
2. To obtain the next binary digit, perform an exclusive-OR-operation between the bit just written down and the next gray code bit. Write down the result.

3. Repeat step 2 until all gray code bits have been exclusive-ORed with binary digits.

Ex. 1.7.18 Convert gray code 101011 into its binary equivalent.

Sol. :

 (1 0 1 0 1 l) _gray = (1 1 0 0 1 0)₂

In general we can perform gray code to binary code conversion as follows 

c. Binary to Gray Code Conversion

Steps for binary to gray code conversion

1. The MSB of the gray code is the same as the MSB of the binary number. So write down MSB as it is.

2. To obtain the next gray digit, perform an exclusive-OR-operation between previous and current binary bit. Write down the result.

3. Repeat step 2 until all binary bits have been exclusive-ORed with their previous ones.

Ex. 1.7.19 Convert 10111011 in binary into its equivalent gray code.

Sol. :

Ex. 1.7.20 Convert binary number 1011100010 to its gray code.

Sol. :

6. Five-bit BCD codes

 • Table 1.7.9 shows some 5-bit BCD codes having special characteristics. These special characteristics of the code are useful for error detection. As shown in the Table 1.7.9, 63210 and two-out-of-five codes have two 1s in every code group. The 63210 code is a weighted code (except for decimal digit 0) and it is used for storing data on magnetic tape. On the other hand two-out-of-five code is unweighted code and is used in the telephone and communications industries. Shift counter code, also known as Johnson code, and 51111 code has specific sequences of 1s which are useful for error detection.

7. Alphanumeric Codes

• The codes which consists of both numbers and alphabetic characters are called alphanumeric codes.

• The most commonly used alphanumeric codes are : ASCII (American Standard Code for Information Interchange) and EBCDIC (Extended Binary Coded Decimal Interchange Code).

• These codes consists of symbols to represent -

* 26 alphabets with capital and small letters.

* Numbers from 0 to 9.

* Punctuation marks and other symbols.

a. ASCII

• ASCII code is a seven-bit code in which the decimal digits are represented by the BCD code preceded by 011.

• Since it is a 7-bit code, it represent 2⁷ = 128 symbols.

• Capital A to Z alphabets are represented by 41 to 5A (7-bit) codes, respectively. For example, ASCII code for A = 41, B = 42, C = 43 and so on.

• Small a to z alphabets are represented by 61 to 6A (7-bit) codes, respectively. For example, a = 61, b = 62, c = 63 and so on.

Ex. 1.7.21 Write the ASCII code for 'ELECTRONICS'.

Sol. : 45, 4C, 45, 43, 54, 52, 4F, 4E, 49, 43, 53

i.e., 1000101 1001100 1000101 1000011 1010100 1010010

1001111 1001110 1001001 1000011 1010011 

Ex. 1.7.22 Encode the word ‘BINARY’ in ASCII form.

Sol.

Examples for Practice  

Ex. 1.7.23   Find gray codes for the following binary numbers :

i) 11001100          ii) 01011110        

[Ans.: i) 10101010 ii) 01110001]

Ex. 1.7.24   What will be the gray code of binary number 1100 B, 0111 B and 1101 B ?    

[Ans.: 1010, 0100,1011]

Ex. 1.7.25   Explain ASCII code and convert NMU JALGAON into its equivalent ASCII code.