Binary Search Tree

Binary Search Tree

AU: Dec.-18,19, Marks 13

Binary search tree is a binary tree in which the nodes are arranged in specific order. That means the values at left subtree are less than the root node value. Similarly the values at the right subtree are greater than the root node. Fig. 5.6.1 represents the binary search tree.

The binary search tree is based on binary search algorithm.

 

1. Operations on Binary Search Tree

1. Insertion of a node in a binary tree

Algorithm:

1. Read the value for the node which is to be created and store it in a node called New.

2. Initially if (root!=NULL) then root-New.

3. Again read the next value of node created in New.

4. If (New->value < root->value) then attach New node as a left child of root otherwise attach New node as a right child of root.

5. Repeat steps 3 aand 4 for constructing required binary search tree completely.

void insert(node *root,node *New)

{

if(New->data <root->data)

{

if(root->left== NULL) ← Attaching left node to the current node.

root->left=New;

else

insert(root->left,New);

}

if(New->data>root->data)

{

if(root->right == NULL)

root->right=New; ← If the root node has already some left child, then move onto left subtree.

else

insert(root->right,New);

srit aupaib au fo

}

}

While inserting any node in binary search tree, first of all we have to look for its appropriate position in the binary search tree. We start comparing this new node with each node of the tree. If the value of the node which is to be inserted is greater than the otolob totes a value of current node we move onto the right subbranch otherwise we move onto the left subbranch. As soon as the appropriate position is found we attach this new node as left or right child appropriately.

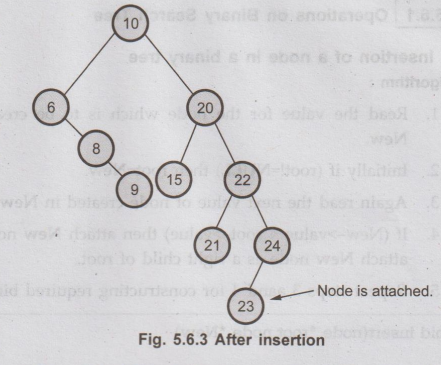
In the Fig. 5.6.2 if we want to insert 23. Then we will start comparing 23 with value of root node i.e. 6. As 23 is greater than 10, will will move on right subtree. Now we will compare 23 with 20 and move right, compare 23 with 22 and move right. Now compare 23 with 24 but it is less than 24. We will move on left branch of 24. But as there is NULL node as left child of 24, we can attach 23 as left child of 24.

2. Deletion of an element from the binary tree

For deletion of any node from binary search tree there are three cases which are possible.

i. Deletion of leaf node.

ii. Deletion of a node having one child.

iii. Deletion of a node having two children.

Let us discuss the above cases one by one.

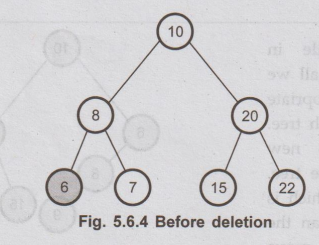
i. Deletion of leaf node

This is the simplest deletion, in which we set the left or right pointer of parent node as NULL.

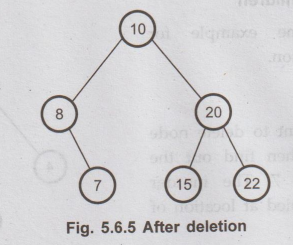
From the above tree, we want to delete the node having value 6 then we will set left pointer of its parent node as NULL. That is left pointer of node having value 8 is set to NULL.

ii. Deletion of a node having one child

To explain this kind of deletion, consider a tree as shown in the Fig. 5.6.6.

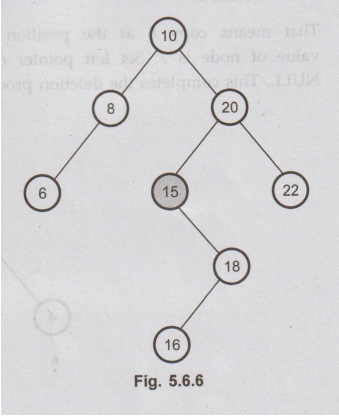
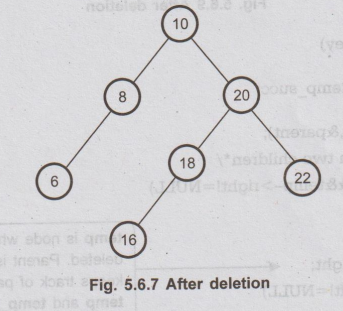
If we want to delete the node 15, then we will simply copy node 18 at place of 15 and then set the node free. The inorder successor is always copied at the position of a node being deleted.

iii. The node having two children

Again, let us take some example for discussing this kind of deletion.

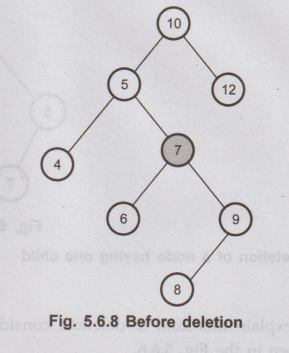
Let us consider that we want to delete node having value 7. We will then find out the inorder successor of node 7. The inorder successor will be simply copied at location of node 7. Thats it!

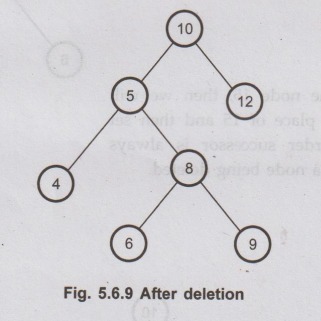
That means copy 8 at the position where value of node is 7. Set left pointer of 9 as NULL. This completes the deletion procedure.

void del(node *root,int key)

{

node *temp, *parent,*temp_succ

temp=search(root,key,&parent);

/*deleting a node with two children*/

if(temp->left!= NULL&&temp->right!= NULL)

{

parent=temp;

temp_succ=temp->right; ← temp is node which is to be deleted. Parent is a node which keeps track of parent of node temp and temp_succ is for keeping track of success of temp.

while(temp_succ->left!= NULL)

{

parent=temp_succ;

temp_succ=temp_succ->left;  ← Moving to leftmost subtree

}

temp->data=temp_succ->data; ← Copying the successor node's data to temp node. Thus content of temp node gets deleted.

if(temp_succ == parent->left)

parent->left = NULL;

else

parent->right = NULL;

printf(" Now Deleted it!");

return;

}

/* deleting a node having only one child*/

/*The node to be deleted has left child*/

if(temp->left!= NULL &&temp->right == NULL)

{

if(parent->left==temp)

parent->left=temp->left; ← Finding parent of temp

else

parent->right-temp->left;

temp=NULL;

free(temp);

printf(" Now Deleted it!");

return;

}

/*The node to be deleted has right child*/

 if(temp->left==NULL &&temp->right!= NULL)

{

if(parent->left == temp)

parent->left-temp->right;

else

parent->right-temp->right;

temp=NULL;

free(temp);

printf(" Now Deleted it!");

return;

}

/*deleting a node which is having no child*/

if(temp->left==NULL &&temp->right == NULL)

{

3. Searching a node from binary search tree

In searching, the node which we want to search is called a key node. The key node will be compared with each node starting from root node if value of key node is greater than current node then we search for it on right subbranch otherwise on left subbranch. If we reach to leaf node and still we do not get the value of key node then we declare "node is not present in the tree".

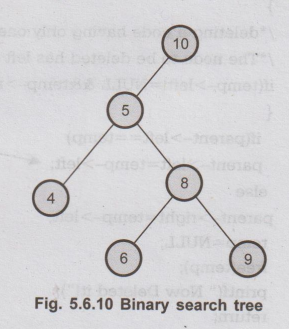
In the above tree, if we want to search for value 9. Then we will compare 9 with root node 10. As 9 is less than 10 we will search on left subbranch. Now compare 9 with 5, but 9 is greater than 5. So we will move on right subbranch. Now compare 9 with 8 but as 9 is greater than 8 we will move on right subbranch. Now we read the node value as 9. Thus the desired node can be searched. Let us see the 'C' implementation of it.

The routine is as given below -

Non-recursive search routine

node *search(node *root,int key,node **parent)

{

node *temp;

temp=root;

while(temp!= NULL)

{

if(temp->data==key)

{

printf("\n The %d Element is Present",temp->data);

return temp;

*parent=temp; ← via to mexport/a/, Mang

if(temp->data>key) ← if current node is greater than key

temp-temp->left; ← Search for the left subtree.

else

temp-temp->right;

}

return NULL;

}

We can display a tree in inorder fashion. Hence the complete implementation is given below along with appropriate output.

/*****************************************

Program for Implementation of Binary Search Tree and

perform insertion deletion, searching, display of tree.

*****************************************/

#include <stdio.h>

#include <conio.h>

#include <stdlib.h>

 

typedef struct bst

{

int data;

struct bst *left, *right;

}node;

 

void insert(node *,node *);

void inorder(node *);

node *search(node *,int,node **);

void del(node *,int);

 

void main()

{

int choice;

char ans='N';

int key;

node *New,*root, *tmp, *parent;

node *get_node();

root = NULL;

clrscr();

printf("\n\t Program For Binary Search Tree ");

do

{

printf("\n1.Create\n2.Search\n3.Delete\n4.Display");

printf("\n\n Enter your choice :");

scanf("%d", &choice);

switch(choice)

{

case 1:do

{

New get_node();

printf("\n Enter The Element ");

scanf("%d", &New->data);

if(root == NULL) /* Tree is not Created */

root=New;

else

insert(root,New);

printf("\n Do u Want To enter More Elements?(y/n)");

ans=getch();;

}while(ans= ='y');

break;

case 2:printf("\n Enter The Element Which You Want To Search");

scanf("%d", &key);

tmp=search(root,key,&parent);

printf("\n Parent of node %d is %d",

tmp->data,parent->data);

break;

case 3:printf("\n Enter The Element U wish to Delete");

scanf("%d", &key);

del(root,key);

break;

case 4:if(root == NULL)

printf("Tree Is Not Created");

else

{

printf("\n The Tree is: ");

inorder(root);

}

break;

}

}while(choice!=5);

}

node *get_node()

{

node *temp;

temp (node *)malloc(sizeof(node));

temp->left=NULL;

temp->right=NULL;

return temp;

}

/*This function is for creating a binary search tree */

void insert(node *root,node *New)

{

if(New->data <root->data)

{

if(root->left== NULL)

root->left=New;

else

insert(root->left,New);

}

if(New->data>root->data)

{

if(root->right == NULL)

root->right=New;

else

insert(root->right,New);

}

}

/*

This function is for searching the node from binary Search Tree

*/

node *search(node *root,int key,node **parent)

{

node *temp;

temp=root;

while(temp!= NULL)

{

if(temp->data= =key)

{

printf("\n The %d Element is Present",temp->data);

return temp;

}

*parent=temp;

if(temp->data>key)

temp-temp->left;

else

temp-temp->right;

}

return NULL;

}

/*

This function is for deleting a node from binary search tree. There exists three possible cases for deletion of a node

*/

void del(node *root,int key)

{

node *temp, *parent,*temp_succ;

temp=search(root,key,&parent);

/*deleting a node with two children*/

if(temp->left!= NULL&&temp->right!= NULL)

{

parent=temp;

temp_succ-temp->right;

while(temp_succ->left!= NULL)

{

parent=temp_succ;

temp_succ=temp_succ->left; ← Finding successor node of temp node

}

temp->data=temp_succ->data;. ← Copy the data of successor node to temp node

if(temp_succ = = parent->left)

parent->left = NULL;

else

parent->right = NULL;

printf(" Now Deleted it!");

return;

}

/*deleting a node having only one child*/

/*The node to be deleted has left child*/

if(temp->left!= NULL &&temp->right= = NULL)

{

if(parent->left == temp)

parent->left=temp->left;

else

parent->right-temp->left;

temp=NULL;

free(temp);

printf(" Now Deleted it!");

return;

}

/*The node to be deleted has right child*/

if(temp->left== NULL &&temp->right!= NULL)

{

if(parent->left == temp)

parent->left-temp->right; ← Parent's left child is deleted.

else

parent->right-temp->right;

temp=NULL;

free(temp);

printf(" Now Deleted it!");

return;

}

/*deleting a node which is having no child*/

if(temp->left==NULL &&temp->right == NULL)

:{

if(parent->left= =temp)

parent->left= NULL;

else

parent->right=NULL; ← Simply make parent's left pointer NULL, so that left child of parent is deleted.

printf(" Now Deleted it!");

return;

}

}

/*

This function displays the tree in inorder fashion

 */

void inorder(node *temp)

{

if(temp!= NULL)

{

inorder(temp->left);

printf("%d",temp->data);

inorder(temp->right);

}

}

Output

Program For Binary Search Tree

1. Create

2. Search

3. Delete

4. Display

Enter your choice :1

Enter The Element 10

Do u Want To enter More Elements?(y/n)

Enter The Element 8

Do u Want To enter More Elements?(y/n)

Enter The Element 9

Do u Want To enter More Elements?(y/n)

Enter The Element 7

Do u Want To enter More Elements?(y/n)

Enter The Element 15

Do u Want To enter More Elements?(y/n)

Enter The Element 13

Do u Want To enter More Elements?(y/n)

Enter The Element 14

Do u Want To enter More Elements? (y/n)

Enter The Element 12

Do u Want To enter More Elements? (y/n)

Enter The Element 16

Do u Want To enter More Elements? (y/n)

1. Create

2. Search

3. Delete

4. Display

 

Enter your choice :4

 

The Tree is: 7  8  9  10  12  13  14  15  16

1. Create

2. Search

3. Delete

4. Display

 

Enter your choice :2

 

Enter The Element Which You Want To Search16

 

The 16 Element is Present

Parent of node 16 is 15

1. Create

2. Search

3. Delete

4. Display

 

Ex. 5.6.1 Define binary search tree. Draw the binary search tree for the following input. 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

Sol. Binary Search Tree (Refer section 5.6)

 

Ex. 5.6.2 Define a binary search tree and construct a binary search tree. With elements {22, 28, 20, 25, 22, 15, 18, 10, 14). Give recursive search algorithm to search an element in that tree.

Sol. Binary Search Tree (Refer section 5.6)

Example

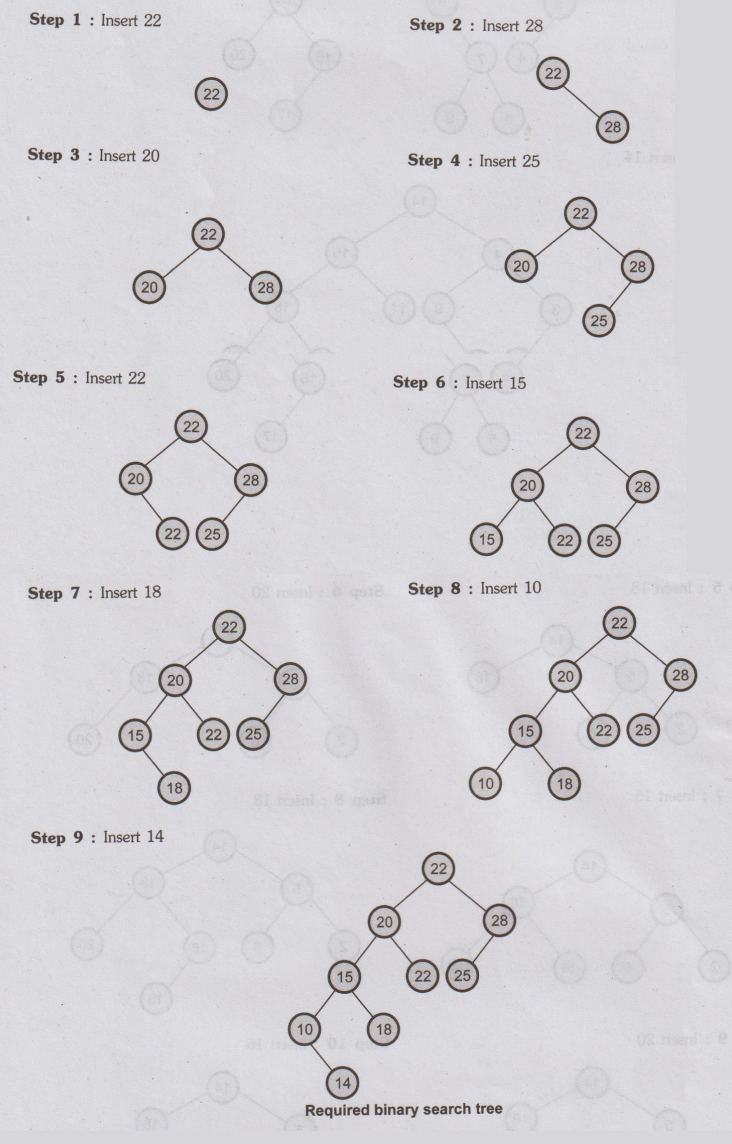
Recursive Algorithm for search - Refer example 5.6.4.

 

Ex. 5.6.3: What is binary search tree? Draw the binary search tree for the following input. 14, 5, 6, 2, 18, 20, 16, 18, -1, 21.

Sol. Binary Search Tree : Refer section 5.6.

Example

Ex. 5.6.4: What is binary search tree? Write a recursive search routine for binary search tree.

Sol. Binary Search Tree: Refer section 5.6.

Recursive Search Routine

node *search(node temp, int key)

{

if (temp == NULL || key == temp.data)

return temp;

else

if (key<temp.data)

return search(temp->left, key);

else

return search(temp->right,key);

}

 

Ex. 5.6.5 Write the following routines to implement the basic binary search tree operations

AU: Dec.-18, Marks 13

 (i) Perform search operation in binary search tree signs

(ii) Find_min and Find_max

Sol.: (i) Search operation - Refer section 5.6.1.

(ii) Find_min and Find_max

Consider following binary search tree

For finding the minimum value from the binary search tree, we need to traverse to the left most node. Hence the left most node in above Fig. 5.6.11 is with value 7 which is the minimum value. Note that for the leftmost node the left pointer is NULL.

The routine for finding the minimum value from the binary search tree is,

Find_min(node *root)

{

struct node* current=root;

while(current->left != NULL)

current=current->left;

printf("%d", current->data);

}

For finding the maximum value from the binary search tree, we need to traverse to the right most node. Hence the right most node in above Fig. 5.6.11 is with value 13 which is the maximum value. Note that for the rightmost node the right pointer is NULL. The routine for finding the maximum value from the binary search tree is Find_max(node *root)

{

struct node* current=root;

while(current->right != NULL)

current-current->right;

printf("%d", current->data);

}

Review Questions

1. Write a iterative search routine for a binary search tree.

2. Describe the binary search tree with an example. Write a iterative function to search for the key value in binary search tree. esmito giarollo sit stiW 2.8.2

3. How to insert and delete an element into binary search tree and write down the code for the insertion routine with an example. dose grandi moitos

AU: Dec.-19, Marks 13