Binomial distribution: Examples Solved Problems

Example 1.7.1

The mean of a Binomial distribution is 20 and S.D is 4. Determine the parameters of the distribution.P [A.U. M/J 2006, A/M 2018 R-13]

Solution: Given: Mean = np = 20... (1)

S.D = √npq = 4

npq = 16..(2)

To find : n,p

(2)/)(1) ⇒npq/np = q = 16/20 = 4/5

p  = 1 - q = 1 - 4/5 = 1/5

(1) ⇒ n(1/5) = 20 ⇒ n =100

The parameters of the binomial distribution are n,p

Here, n = 100, p = 1/5

Example 1.7.2

Comment on the following:

The mean of a binomial distribution is 3 and variance is 4.

Solution: Mean = 3 and variance = 4

 np = 3 and  npq 4, i.e., 3q = 4; q =  4 / 3 > 1

Which is impossible since q being a probability of an event, 0 < q < 1, But q > 1.

 The given data cannot determine a binomial distribution.

Example 1.7.3

In a binomial distribution consisting of 5 independent trials, probability of 1 and 2 successes are 0.4096 and 0.2048 respectively. Find the parameter P of the distribution.

Solution: Given: n = 5 , P(1) = 0.4096 , P(2) = 0.2048

P(x) = nCxpx qn - x

To find: p

P (1) = 5 C1pq4 = 5pq4 = 0.4096

P (2) = 5C2p2q3 = 10p2 q3 = 0.2048

P(2) / P(1) ⇒ 10p2q3 / 5pq4 = 0.2048/0.4096

⇒ 2p/q = 1/2 ⇒ p/q = 1/4

⇒ 4p = q ⇒ 4p = 1 - p

⇒ 5p = 1 ⇒ p = 1/5

Example 1.7.4

The mean and variance of a binomial variate are 8 and 6. Find P (X≥2) [A.U Tvli A/M 2009]

Solution: Given: Mean = np = 8 ....(1)

Variance = npq = 6 ....(2)

(2) / (1) ⇒ npq/np ⇒ q = 6/8 = 3/4

P = 1 – q = 1 – 3/4 = 1/4

(1) = n(1/4) = 8 ⇒ n = 32

P(x) = nCPxqn - x

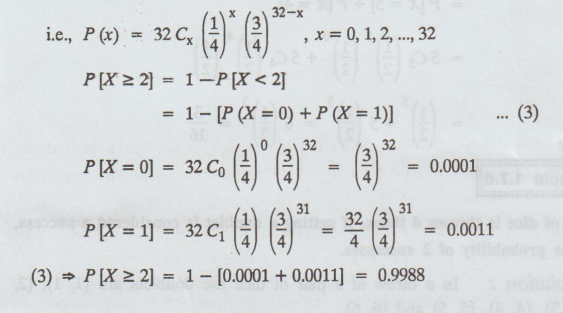
 (3) ⇒ P(X ≥ 2] = 1 [0.0001 + 0.0011] = 0.9988

Example 1.7.5

Find the probability that in tossing a fair coin 5 times, there will appear (a) 3 heads (b) 3 tails and 2 heads (c) atleast 1 head and (d) not more than 1 tail.

Solution: Given: p = ½ , q =  ½ , n =5

Let X denote number of heads

(1)(a) P [3 heads] = P[X = 3]

= 5 C3(1/2)3(1/2)2 = (10) (1/2)2 = 5/16

 (b) P [3 tails and 2 heads]

= P[X = 2] = 5C2(1/2)2(1/2)3 = 5/16

 (c) P [atleast 1 head] = P[X≥ 1]

= 1-P[X < 1]

= 1-P(X = 0]

= 1-5 C0(1/2)0(1/2)5 = 31/32

 (d) P [not more than 1 tail]

= P [0 tail] + P [1 tail]

= P [5 head] + P [4 head]

= P(X = 5] + P(X = 4]

= 5 C5(1/2)5(1/2)0 + 5C4 (1/2)4(1/2)

= (1/2)5 + 5(1/2)5 = 6 (1/2)5  = 3/16

Example 1.7.6

A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of 2 successes.

Solution: In a throw of a pair of dice the doublets are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6).

p = probability of getting a doublet = 6/36 = 1/6

and q = 1 - p = 1 – 6/5 = 5

P (X = x) = 4Cx (1/6)x(5/6)4 - x

Probability of 2 successes = p(X = 2 ) = 4C2(1/2)2(5/6)2 = 6 × 1/36 × 25/36 = 25/216

Example 1.7.7

A machine manufacturing screws is known to produce 5% defective. In a random sample of 15 screws, what is the probability that there are (i) exactly 3 defectives; (ii) not more than 3 defectives.

[AU N/D 2008] [A.U CBT N/D 2011] [A.U N/D 2018 R-17 PS]

Solution: p = probability that a screw is defective = 5/100

q = 1- p = 1- 5/100 = 95/100 and n = 15

Let X denote the number of defectives.

(i) P(exactly 3 defectives) P (X = 3) 5

= 15C3 (5/100)3 ( 95/100)12  = 0.0307

 (ii) P(not more than 3 defectives) = P (X ≤ 3)

=  P(X = 0) +  P(X = 1) + P(X = 2) + P(X = 3)

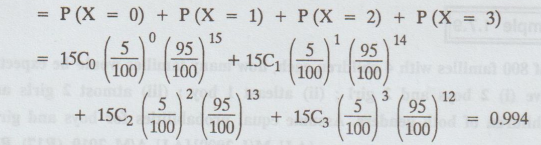
Example 1.7.8

If 10% of the screws produced by an automatic machine are defective, find the probability that of 20 screws selected at random, there are (i) exactly two defectives (ii) atmost three defectives (iii) atleast two defectives and (iv) between one and three defectives (inclusive)  [AU Dec. 2007]

Solution :

p = Probability that a screw is defective = 10/100 = 0.1

q = 1 - p = 1 - 0.1 = 1 – 10/100 = 9/10 and n = 20

. P (X = x) = 20Cx(1/10)x(9/10)20-x , x = 0, 1, 2, ... 20

Let X denote the number of defectives.

 (iv) Probability that the number of defectives is between one and three (inclusive)

= P(1 ≤  X  ≤3) P(X = 1) + P(X = 2) + P(X = 3)

=917/1020 (4470)

Example 1.7.9

Out of 800 families with 4 children each, how many families would be expected to have (i) 2 boys and 2 girl; (ii) atleast 1 boy; (iii) atmost 2 girls and (iv) children of both genders. Assume equal probabilities for boys and girls. [A.U M/J 2009] [A.U A/M 2019 (R17) RP]

Solution: Considering each child is a trial, n = 4. Assuming that birth of a boy is a success, p = 1/2 and q = 1/2

Let 'X' denote the number of successes (boys).

 (i) P (2 boys and 2 girls) P (X = 2) = 4C2(1/2)2 (1/2)4 - 2

=4C2(1/2)2 (1/2)2 = 6 1/24 = 3/8

Number of families having 2 boys and 2 girls = 800 × 3/8 = 300

 (ii) P (atleast 1 boy) = P(X  ≥ 1) 1)

= 1 - P(X < 1) = 1 - P (X = 0)

=1 4C0(1/2)4 = 1- (1/2)4 = 15/16

Number of families having atleast 1 boy = 800 × 15/16 = 750

(iii) P(atmost 2 girls) = P[atleast 2 boys]

= P[X≥2] = 1-P [X < 2]

= 1- [P (X = 0) + P(X = 1)]

= 1- [4C0(1/2)0 (1/2)4 + 4C1(1/2)1 (1/2)3]

= 1 – [ (1/2)4 + 4(1/2)4] = 1 – 5/16 = 11/16

 Number of families having atmost 2 girls = 800 × 11/16 = 550

 (iv) P(children of both genders) = 1 - P(children of the same gender)

= 1 [P(all are boys) + P(all are girls)]

= 1- [P (X = 4) + P(X = 0)]

= 1- [4C4(1/2)4 (1/2)0 + 4C0(1/2)0 (1/2)4]

= 1 – 2(1/2)4 = 1 – 1/8 = 7/8

 The number of families having children of both gender = 800 × 7/8 = 700

Example 1.7.10

In a large consignment of electric bulb 10% are defective. A random sample of 20 is taken for inspection. Find the probability that (i) All are good bulbs (ii) Atmost there are 3 defective bulbs (iii) Exactly there are 3 defective bulbs. [A.U CBT M/J 2010] [A.U A/M 2013]

Solution: p→ Probability that an electric bulb is defective = 1/10

q = 1 - p = 1 – 1/10 = 9/10 and n = 20

Let X denote the number of defectives.

(i) P(All are good) = P(none of them are defective)

= P(X = 0) = 20C0(1/10)0 (9/10)20

=  (9/10)20 = 0.1216

 (ii) P(Atmost three are defective) P(X ≤ 3)

= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)

= 20C0(1/10)0 (9/10)20 + 20C1(1/10)1 (9/10)19 + 20C2(1/10)2 (9/10)18 +20C3(1/10)3 (9/10)17

= 0.8666

 (iii) P(Exactly 3 are defective) = P(X = 3)

= 20C3(1/10)3 (9/10)17

= 0.19

Example 1.7.11

Suppose that P(X=0) = 1− P(X = 1). If E(X) = 3 Var (X), find P(X=0).

Solution :

Given P[X = 0] = 1-P [X = 1]

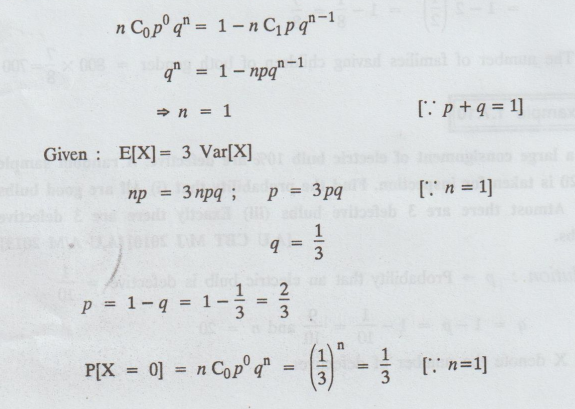
Example 1.7.12

If X is a binomial random variable with expected value 6 and variance 2.4, find P(X = 5)

Solution : We know that, E [X] = np

Var [X] = npq

Given: np = 6....(1)

npq = 2.4 ....(2)

(2/(1) = npq/np = 2.4/6 = 0.4 i.e, = 0.4

p = 1 - q = 1 – 0.4 = 0.6

(1) ⇒ np = 6 ; n(0.6) = 6; n = 10

Formula P(x) = ncxpx q(n − x)

P(X = 5) =  p (5) =10C5(0.6)5 (0.4)5

Example 1.7.13

The probability of a bomb hitting a target 1/5 is Two bombs are enough to destroy a bridge. If six bombs are aimed at the bridge, find the probability that the bridge is destroyed? [AU, Dec, '98] [A.U M/J 2014]

Solution:

Let 'p' denoted the probability of a bomb hitting the target.

Given: p = 1/5; q = 1 – p =  1 – 1/5 = 4/5 and n = 6

Let X denotes the number of bombs to destroy a bridge.

the R.V X follows a binomial distribution with parameters

n = 6 & p= 1/5 and is denoted by X ~ B (n, p)

i.e., X ~ B (6,1/5)

 To find P (X = 2)

The probability distribution is given by,

P(X = x) = nCxpx qn - x, x = 0, 1, ... n

 P(X=2) = 6C2(1/5)2(4/5)4 = 6.5/1.2 × 1/5.5 . 4.4.4.4/5.5.5.5

= 768/3125 = 0.2458

Example 1.7.14

If X follows B (3, 1/3) and Y follows B (5, 1/3) find P(X + Y≥ 1). [AU Dec. 2005]

Solution :

Given n1= 3, n2 = 5,  p = 1/3 , q = 2/3

 X + Y follows B [ 3 + 5, 1/3 ] = b [ 8,1/3]

P(X + Y =  x) = 8Cx (1/3)x (2/3)8 - x

P[X + Y ≥ 1] = 1− P [X + Y < 1]

= 1-P [X + Y = 0]

=1 – [2/3]8 = 0.961

Example 1.7.15

If the m.g.f of a random variable X is of the form (0.4et + 0.6)8, what is the m.g.f of 3X + 2. Evaluate E [X].

Solution:

We know that, MX (t) = (q + pet)n ....(1)

Given: (0.4 et +0.6)8 we can write

(0.6+0.4 et)8 compare with (1) we get

q = 0.6, p = 0.4, n = 8

E[X]= np = 8 (0.4) = 32

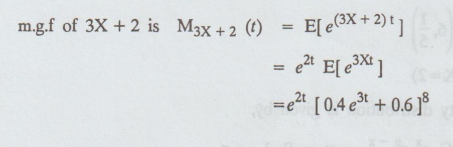
Example 1.7.16

During war, one ship out of nine was sunk on an average in making a certain voyage. What was the probability that exactly 3 out of a convoy of 6 ships would arrive safely.

Solution: Probability (ship sinks) = p = 1/9

 q = 1 - p = 1 - 1/9 = 8/9 ; n = 6

 P(X) = 6Cx px q6-x, x = 0, 1, 2, ..., 6

P(3 out of 6 ships arrive safely)

= P(X = 6 - 3 = 3 ships would sink)

= 6C3 p3 q6-3

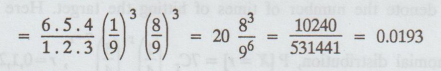
= 10240/531441 = 0.0193

Example 1.7.17

6 dice are thrown 729 times. How many times do you expect atleast three dice to show 5 or 6 ? [A.U. N/D 2003, M/J 2004] [A.U N/D 2013] [A.U A/M 2018 R-08]

Solution :

The probability of getting 5 or 6 when a die is thrown = 2/6 = 1/3

p= 1/3 ; q=1 – p = 1- 1/3 = 2/3  and n = 6

P (X = x) = 6Cx (1/3)x(2/3)6-x , x = 0,1,...6

The probability of getting atleast 3 dice to show 5 or 6 is,

= P(X ≥ ) = P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)

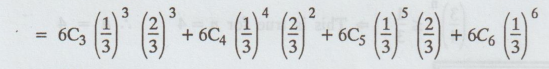
= 233/729

In 729 times, when 6 dice are thrown,

 = 729 × 233/729 = 233times

In 233 times atleast 3 dice to show 5 or 6.

Example 1.7.18

The probability of a man hitting a target is 1/4. (i) If he fires 7 times, what is the probability of his hitting the target atleast twice? (ii) How many times must he fire so that the probability of hitting the target atleast once is greater than 2/3 ? [A.U M/J 2012, A.U A/M 2017 R13]

Solution:

Probability of hitting the target p = 1/4

 q = 1 – p = 3/4

Let X denote the number of times of hitting the target. Here n = 7

By Binomial distribution, P (X = r] = 7Cr (1/4)r (3/4)7-r , r = 0,1,2,...7

(i) P[hitting the target atleast twice]

= P[X≥2] = 1-P[X<2] = 1-[P (0) + P (1)]

Example 1.7.19

A coin having probability p of coming up heads is successively flipped until the rth head appears. Argue that X, the number of flips required will be n, n≥r with probability.

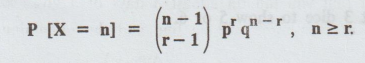[A.U A/M 2010]

Solution: A coin having probability P of coming up heads is successively flipped until th head appears. Argue that X, the number of flips required will be n, n ≥r with probability

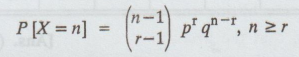
This is negative Binomial distribution.

To prove the statement we first discuss Binomial distribution.

Suppose that n independent trial, each of which result in a success with probability 1-p, are to be performed.

If X represents the number of successes that occur in the n trials, then X is said to be a Binomial random variable with (n, p) is given by

P (X = x) = n Cxpx(1 - p)n - x, x = 0, 1, 2, ... n

In order for X, the first n 1 flips must have r - 1 heads, and then the flip must land heads.

By independent the desired probability is thus

P[X = n] = (n - 1)Cr - 1 pn - 1 (1 - p) n – r p

= (n - 1)Cr - 1 pn (1 - p) n – r