Biot-Savart Law

Biot-Savart Law

AU : Dec.-03,07,09,10,13, May-04,07,09,10,11

• Consider a conductor carrying a direct current I and a steady magnetic field produced around it. The Biot-Savart law allows us to obtain the differential magnetic field intensity produced at a point P, due to a differential current element IdL. The current carrying conductor is shown in the Fig. 7.3.1.

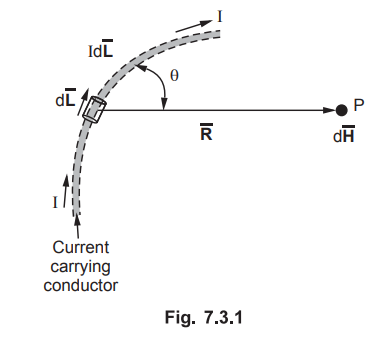
Consider a differential length dL hence the differential current element is IdL. This is very small part of the current carying conductor. The point P is at a distance R from the differential current element. The θ is the angle between the differential current element and the line joining point P to the differential current element.

• The Biot-Savart law states that,

• The magnetic field intensity  produced at a point P due to a differential current element IdL is,

1. Proportional to the product of the current I and differential length dL.

2. The sine of the angle between the element and the line joining point P to the element.

3. And inversely proportional to the square of the distance R between point P and the element.

• Mathematically, the Biot-Savart law can be stated as,

Let us express this equation in vector form.

Let     dL = Magnitude of vector length and

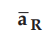 = Unit vector in the direction from differential current element to point P

Then from rule of cross product,

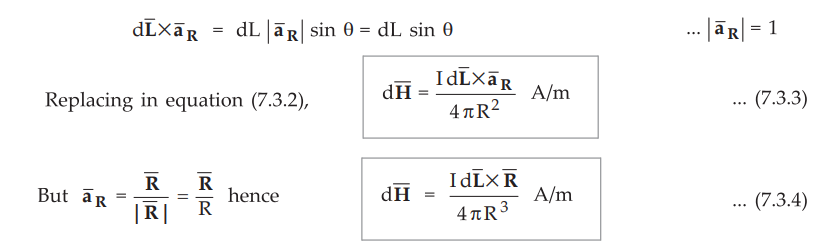
• The equations (7.3.3) and (7.3.4) is the mathematical form of Biot-Savart law.

• According to the direction of cross product, the direction of  is normal to the plane containing two vectors and in that normal direction which is along the progress of right handed screw, turned from  through the smaller angle 0 towards the line joining element to the point P. Thus the direction of  is normal to the plane of paper. For the case considered, according to right handed screw rule, the direction of is going into the plane of the paper.

• The entire conductor is made up of all such differential elements. Hence to obtain total magnetic field intensity , the above equation (7.3.4) takes the integral form as,

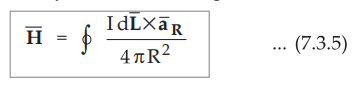
• The closed line integral is required to ensure that all the current elements are considered. This is because current can flow only in the closed path, provided by the closed circuit. If the current element is considered at point 1 and point P at point 2, as shown in the Fig. 7.3.2 then,

This is called integral form of Biot-Savart law.

1. Biot-Savart Law Interms of Distributed Sources

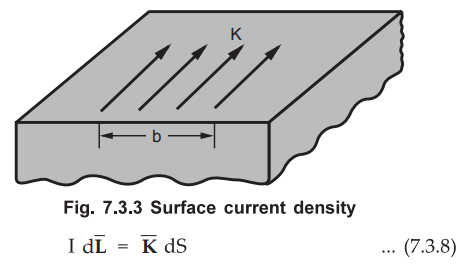
• Consider a surface carrying a uniform current over its surface as shown in the Fig. 7.3.3. Then the surface current density is denoted as  and measured in amperes per metre (A/m). Thus for uniform current density, the current I in any width b is given by I = Kb, where width b is perpendicular to the direction of current flow.

•  Thus if dS is the differential surface area considered of a surface having current density  then,

• If the current density in a volume of a given conductor is  measured in A / m² then for a differential volume dv we can write,

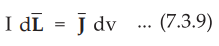
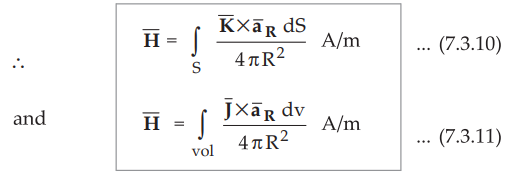
• Hence the Biot-Savart law can be expressed for surface current considering  dS while for volume current considering  dv.

• The Biot-Savart law is also called Ampere's law for the current element.

Ex. 7.3.1 Find the magnetic flux density at the centre 'P' of a square of sides equal to 5m and carrying 10 amperes of current.

AU : Dec.-03, 07, Marks 16, Hay-09, Marks 8

Sol. : The square is placed in the xy plane as shown in the Fig. 7.3.4.

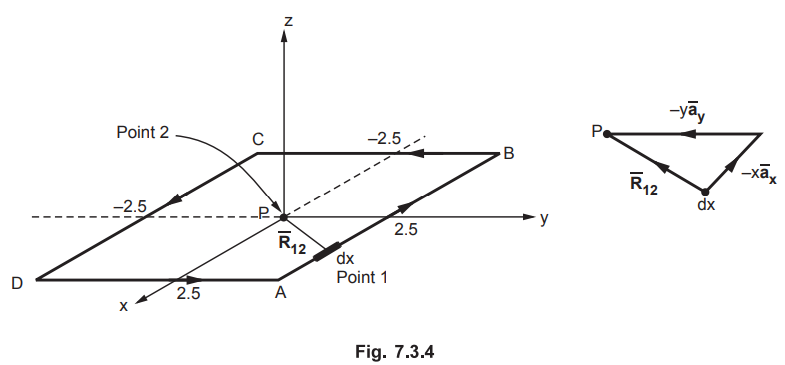
Consider differential element dx along AB of the square.

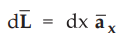
The  joining differential element to point P is,

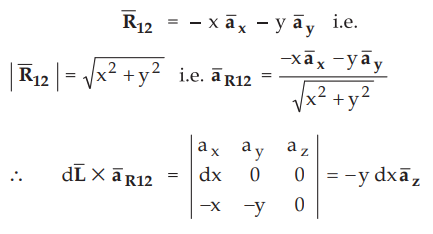
According to Biot-Savart law,

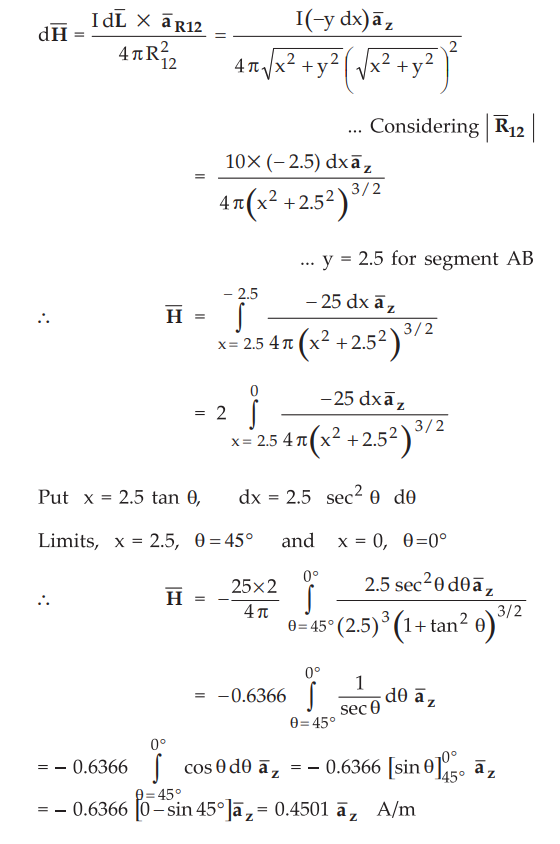
This  is due to the segment AB of the square. All sides will produce same  at point P.

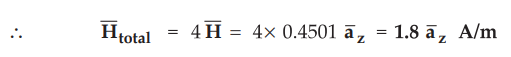
Ex. 7.3.2 Find the magnetic field intensity at the origin due to a current element,

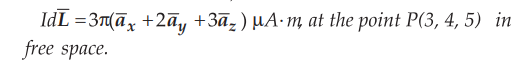
AU : May-07, Marks 10

Sol. :

Examples for Practice

Ex. 7.3.3 Find the incremental field strength at P2 due to the current element of 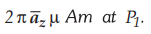 The co-ordinates of P₁ and P₂ are (4,0, 0) and (0, 3, 0) respectively.

Ex. 7.3.4 A wire of length L is formed into a) Circle b) Equilateral triangle and c) Square. For the same current I, find the magnetic field  at the centre of each.

7.3.5 Given points are A (1, 2, 4), B (- 2, - 1, 3) and C (3, 1, - 2). Let the differential current element with I = 6 A and 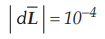 m is located at point A. The direction of  is from A to B. Find   at C.

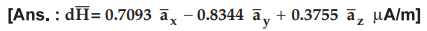
Review Question

1. State and explain Biot-Savart law.

AU : Dec.-03, 09. 10, 13, May-04, 10. 11, Marks 4