Blondel Diagram[Constant Power Circle]

Blondel Diagram[Constant Power Circle]

The Blondel diagram of a synchronous motor is an extension of a simple phasor diagram of a synchronous motor.

For a synchronous motor, the power input to the motor per phase is given by,

p_in = V_Ph I_aph cos ϕ          ...Per phase

The gross mechanical power developed per phase will be equal to the difference between p_in per phase and the per phase copper losses of the winding.

Now consider the phasor diagram as shown in the Fig. 4.16.1.

The equation (4.16.1) represents polar equation to a circle. To obtain this circle in a phasor diagram, draw a line OY at an angle θ with respect to OA.

∠YOA = θ

∠YOB = ϕ

The circle represented by equation (4.16.1) has a centre at some point O' on the line OY. The circle drawn with centre as O' and radius as OTJ represents circle of constant power. This is called Blondel diagram, shown in the Fig. 4.16.2.

Thus if excitation is varied while the power is kept constant, then working point B will move along the circle of constant power.

Let     O’B = Radius of circle = r

OO’= Distant d

Applying cosine rule to triangle OBO',

r² = (OB) ² + (OO') ² - 2 (OB) (OO') cos (OB Λ OO')    ... (4.16.2)

Now OB represents resultant E_R which is I_aZ_s. Thus OB is proportional to current and when referred to OY represents the current in both magnitude and phase.

OB = I_a = I say

Substituting various values in equation (4.16.2) we get,

r²= I² + d² - 2dI cos ϕ

I² - 2d 2dI cos ϕ + (d² r² ) = 0   ...(4.16.3)

Comparing equations (4.16.1) and (4.16.3) we get,

OO’ = d V/2R_a           ...(4.16.4)

Thus the point O' is independent of power P_m and is a constant for a given motor operating at a fixed applied voltage V.

Comparing last term of equations (4.16.1) and (4.16.3),

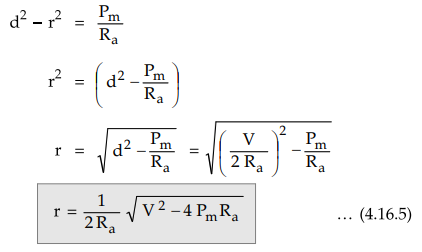
The equation shows that as power P_m must be real, then 4 P_mR_a ≥ V². The maximum possible power per phase is,

4(p_m)max R_a = V₂

(p_m)max = V₂ / 4 R_a        …. (4.16.6)

And the radius of the circle for maximum power is zero. Thus at the time of maximum power, the circle becomes a point O'.

While when the power p_m - O, then

r = V / 2 R_a   = OO’

This shows that the circle of zero power passes through the points O and A.

The radius for any power Pm is given by,

This is generalized expression for the radius for any power P_m       

Review Questions

 1. Explain constant power circle for synchronous motor.

2. Explain how the current locus of a synchronous motor developing constant power is a circle.