Calculating Capacitance using Laplace's Equation

Calculating Capacitance using Laplace's Equation

AU : Dec.-09, 10, May-03, 11, 12

• As mentioned earlier, the Laplace's equation can be used to find the capacitance under various conditions. Let us discuss few examples of calculating capacitance using Laplace's equation.

Key Point : Note that as outer shell is at higher potential,   is directed from outer to inner shell and hence in  direction.

 

Ex. 6.5.1 Solve the Laplace's equation for the potential field in the homogeneous region between the two concentric conducting spheres with radii a and b, such that b>a if potential V = 0 at r = b and V = Vo at r = a. And find the capacitance between the two concentric spheres.

AU : May-11, Marks 8

Sol. : The concentric conductors are shown in the Fig. 6.5.1.

At r = b, V = 0 hence the outer sphere is shown at zero potential.

The field intensity  will be only in radial direction hence V is changing only in radial direction as the radial distance r, and not the function of θ and ϕ According to Laplace's equation,

This is the potential field in the region between the two spheres.

 

As per the boundary conditions between conductor and dielectric, the  is always normal to the surface hence 

Ex. 6.5.2 Use Laplace’s equation to find the capacitance per unit length of a co-axial cable of inner radius 'a' m and outer radius 'b' m. Assume V = V0 at r = a and V = 0 at r = b.

AU : Dec.-09, Marks 16

Sol. : The co-axial cable is shown in the Fig. 6.5.2.

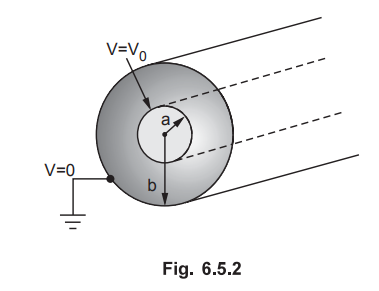
Consider cylindrical co-ordinate system. The field intensity  is in radial direction from inner to outer cylinder hence V is a function of r only and not the function of ϕ and z.

Using Laplace's equation,

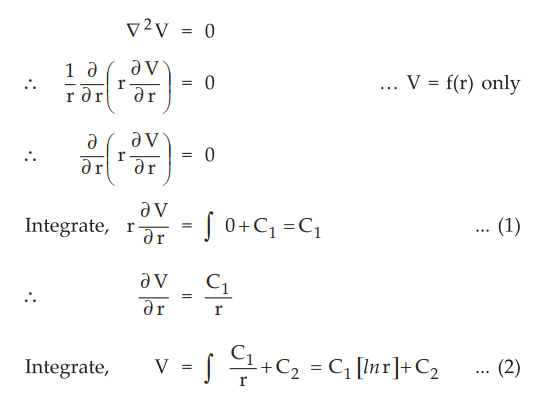
Using boundary conditions, V = 0 at r = b and V = V0 at r = a,

 

Ex. 6.5.3 Solve one dimensional Laplace equation to obtain the field inside a parallel plate capacitor and also find the expression for the surface charge density at two plates. Hence find the capacitance between the parallel plates.

AU : May-03, Marks 16

Sol. : Consider the two parallel plates as shown in the Fig. 6.5.3 with lower plate at V = 0 V and upper plate at V = Vi V. They are separated by distance d. Consider the cylindrical co-ordinates.

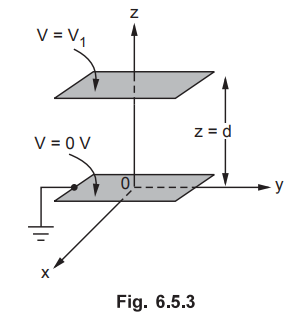
Key Point : Potential V is a function of z alone and is independent of r and ϕ .

The acts in the normal direction as per the boundary conditions. Thus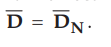 

This is the magnitude of the surface charge densities on the plates. It is positive on the upper plate and negative on the lower plate.

Let surface area of the plate is A.

 

Ex. 6.5.4 Conducting spherical shells with radii a = 8 cm and b = 20 cm are maintained at a potential difference of 100 V such that V(r = b) = 0 and

V = (r = a) = 100 V. Determine V and   in the region between the shells. If Ɛr = 2 in the region determine the total charge induced on the shells and the capacitance of the capacitor.

Sol. : Refer example 6.5.1 for the procedure. Use V0 = 100 V, b = 0.2 m, a = 0.08 m and Ɛr = 2.

Verify the answers as,

 

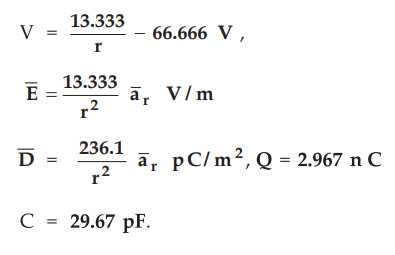
Ex. 6.5.5 Two parallel conducting plates are separated by distance 'd' apart and filled with dielectric medium having 'Ɛr' as relative permittivity. Using Laplace's equation derive an expression for capacitance per unit length of parallel plate capacitor, if it is connected to a DC source supplying 'V' volts.

Sol. : Refer example 6.5.3 and use —1 = V.

ρS = VE / d C/m²

Now let surface area of the plate is A m².

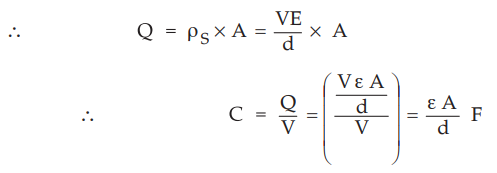
This is the required expression for the capacitance of a parallel plate capacitor.

 

Example for Practice

Ex. 6.5.6 A capacitor of two large horizontal parallel plates has an internal separation 'd' between plates. A dielectric slab of relative permittivity £r and thickness a is placed on the lower plate of capacitor. Neglect edge effects. If the potential difference between the plates is show that the electric - field intensity E1 in the 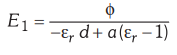 and capacitance C of the arrangement will be :

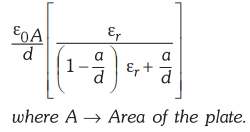
Review Questions

1. Find the expression for the cylindrical capacitance using Laplace’s equation.

2. Obtain the capacitance of parallel plate capacitor using Laplace's equation.

3. Obtain the capacitance of spherical plate capacitor using Laplace’s equation.

4. Obtain the capacitance of co-axial cable capacitor using Laplace's equation.