Transmission and Distribution: Unit III: (a) Mechanical Design of Transmission Lines
Calculation of Diameter for Stranded Conductor
Mechanical Design of Transmission Lines
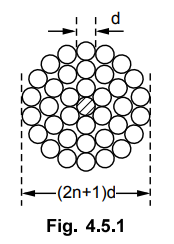
The stranded conductor usually has a central wire which is surrounded by the layers of wires. These layers consists of 6, 12, 18, ...... wires successively. Thus the total strands are 7, 13, 19 ...... .
Calculation of Diameter
for Stranded Conductor
The stranded conductor usually has a
central wire which is surrounded by the layers of wires. These layers consists
of 6, 12, 18, ...... wires successively. Thus the total strands are 7, 13, 19
...... .
Such a stranded conductor with 37
strands is shown in the Fig. 4.5.1.
Let d = Diameter of each strand
Then the total diameter of a stranded
conductor (cable) is given by,
dc = (2 n + 1) d
where n = Number of layers in which the
strands are arranged around central strand.
The stranded conductor is specified as
number of strands and diameter of strand.
For example 7/0.295 mm which indicates 7
strands with 0.295 mm diameter of each strand.
If at all the number of layers are not
specified then the number of layers can be calculated as number of strands and
layers are related to each other by the equation,
x = 3n2 + 3n + 1
where
x - Number of strands
and n
= Number of layers
The standard number of strands in each
successive layer from inner to outer is 6, 12, 18, 24 ...............
Example 4.5.1
A transmission line uses a hard drawn copper of area of cross-section of 200
mm with a conductor 61/2.24 mm. The span of the line is 160 m with supports at
the level. The maximum stress for a conductor is 41 kg/mm with a factor of
safety of 5.
Calculate : a) Sag in still air
b) Sag with a wind pressure of 1.35 kg/m
and ice coating of 1.25 cm.
c) Vertical sag with conditions as in
(b) above
Assume copper density as 8.9 gm/cm3
.
Solution : L - 160 m, Sf - 5,
Maximum stress - 41 kg/mm2
To find maximum stress in conductor, use
area of copper as 200 mm2 .
Maximum stress in kg = 41 × 200 = 8200
kg
Sf = Maximum stress / Tension
T i.e. T = 8200 / 5 = 1640 kg
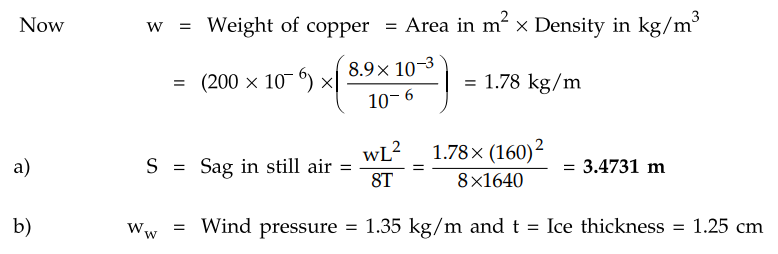
Now we want conductor diameter which is
dc It consists of 61 strands, each of diameter 2.24 mm.

Review Questions
1. An overhead line is supported between two towers 250 m apart
having a difference in their levels equal to 4 m. Calculate the sag at the lower
support if the wind pressure is 39 kg/m of projected area. Factor of safety is
2.
The conductor data is :
Nominal copper area 110 mm2 , stranded conductor 37/2.79
mm
Weight 844 kg/km, ultimate strength 7950 kg
[Ans.: 0.6817 m]
2. A 132 kV transmission line uses ACSR conductor whose data are :
nominal copper area 110 mm2 ; size 30 + 7/2.79 mm; weight 844 kg/km2;
ultimate strength 7950 kg. The line is subjected to a horizontal wind pressure
of 40 kg/m of projected area and 1.25 cm radial ice coating. If the maximum
permissible sag is 6 m, calculate the permissible span between the a two
supports, allowing for a factor of safety of 2. Weight of ice is 915 kg/m3
.
[Ans.: 133.5511 m]
Transmission and Distribution: Unit III: (a) Mechanical Design of Transmission Lines : Tag: : Mechanical Design of Transmission Lines - Calculation of Diameter for Stranded Conductor
Related Topics
Related Subjects
Transmission and Distribution
EE3401 TD 4th Semester EEE Dept | 2021 Regulation | 4th Semester EEE Dept 2021 Regulation
