Calculation of Sag and Tension

Calculation of Sag and Tension

AU : May-04,11,13, Dec.-10,ll,12,13,15,16

Let us see the method of calculation of sag and tension in an overhead transmission line. In practice there are two cases in which sag calculation differs. Such two practical cases are,

1. The supports supporting the conductor are located at equal level.

2. The supports supporting the conductor are located at unequal levels.

 

1. supports at Equal Level

Consider a conductor supported by the supports A and B which are located at same level. This is shown in the Fig. 4.3.1.

The point O is the lowest point on the trajectory. Mathematically it can be proved that point O is at the midspan.

Let

L = Length of span in metres

W = Weight per unit length of the conductor in kg/m

T = Tension in the conductor in kg

Consider a point P on the conductor and let point O is origin. Hence the co-ordinates of point P are (x, y).

The length of span L is large compared to sag S hence the shape of conductor takes the form of parabola.

Let     l = Half span length = L/2

As the curve is very small due to small sag, it can be assumed that the length OP of the conductor is same as the × co-ordinate of point P.

l (OP) = x

Now there are two external forces acting on the portion OP of the conductor,

1. The tension T.

2. The weight wx which acts at a distance of x/2 from the point O or P, as OP = x.

The tension T acts in horizontal direction at point O. 

Taking moments of these two forces about point P and equating them we get,

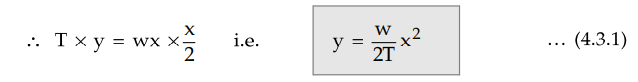
The equation shows that the trajectory is parabolic in nature. At the support A and B, the vertical distance y from the origin O indicates the sag S.

. At A or B, x = l = L/2 and y = S

Substituting in equation (4.3.1),

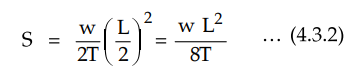
where

L = Total span length and T = Tension in conductor

The sag at any point P of the conductor is

 

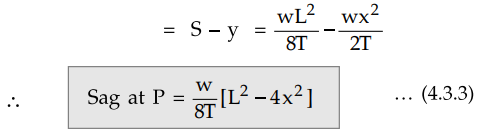
Example 4.3.1 An overhead line has a span of 250 m. The tension in the line is 1500 kg while the conductor weighs 750 kg per 1000 metres. Calculate the maximum sag in the conductor.

Solution: The span L = 250 m and T = 1500 kg

 

2. Supports at Unequal Levels

In many situations, practically it is not possible to have the supports at the same level. It is necessary to use the supports at the different levels in the areas including small hills, river etc.

The Fig. 4.3.2 shows an overhead line supported at the supports A and B which are at the unequal levels.

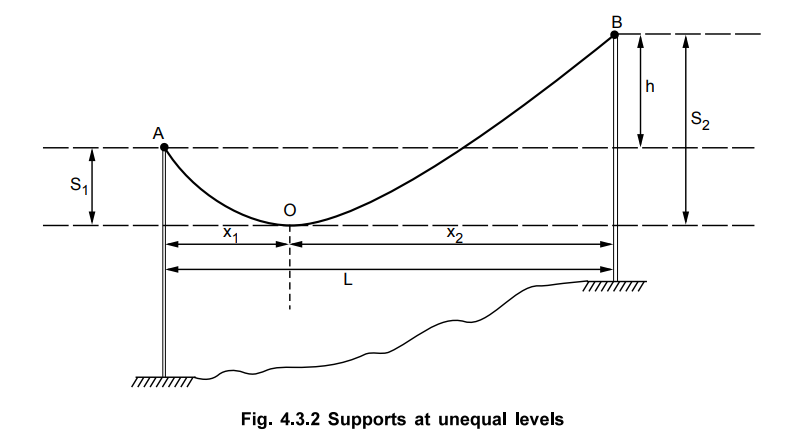
Let     L = Total span length

h = Difference in the levels 

T = Tension in the conductor

x₁ = Distance of point O from the support A

x₂ = Distance of point O from the support B

w = Weight per unit length of the conductor

Applying the results derived in the earlier section, we can write

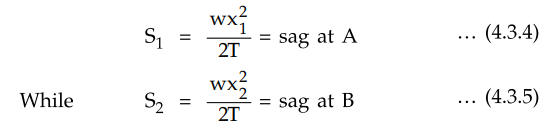
The sum of x₁ and x₂ gives the total span length L.

x₁ + x₂ = L  ... (4.3.6)

If x₁ and x₂ are known, then sags Sx and S2 can be obtained using equations (4.3.4) and (4.3.5).

Subtract equation (4.3.4) from equation (4.3.5),

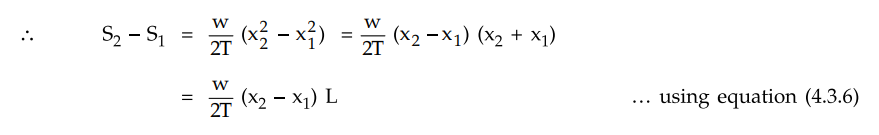
But it can be seen that the distance h which is difference in the levels is also the difference between the two sags S₁ and S₂.

S₂ - S₁ = h

Substituting in the equation of S₂ - S₁

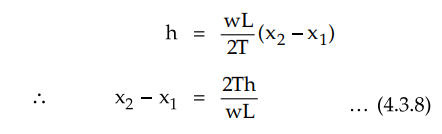
Solving the equations (4.3.6) and (4.3.8) simultaneously we get, 2Th

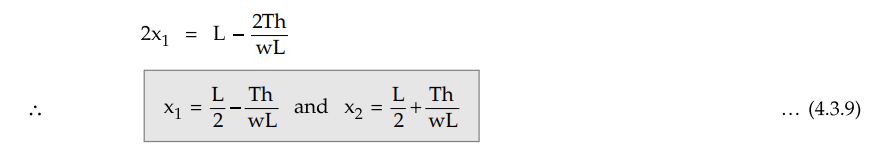
Once the values of x_t and x₂ are known, the sags S₁ and S₂ can be determined.

 

Example 4.3.2 The two towers of height 95 m and 70 m respectively support the line conductor, at a river crossing. The horizontal distance between the towers is 400 m. If the tension in the conductor is 1100 kg and its weight is 0.8 kg/m, calculate

a) Sag at lower support.

b)  Sag at upper support.

c) Clearance of lowest point on trajectory from water level.

Assume bases of towers to be at the water level.

Solution : The towers and the sags are shown in the Fig. 4.3.3.

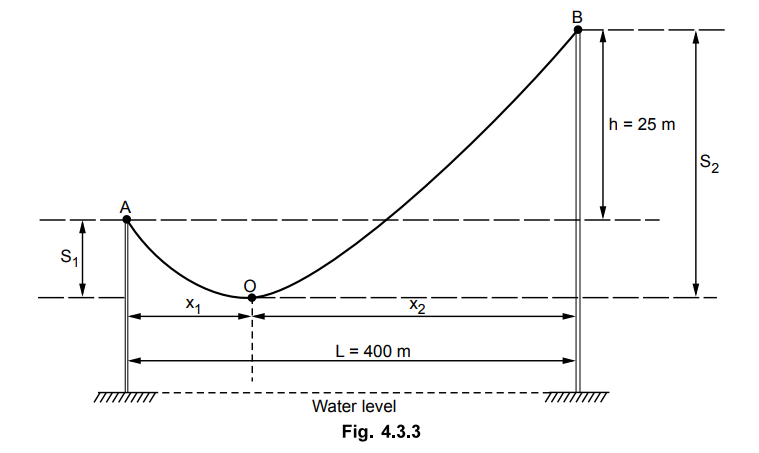
The height of tower A is 70 m while that of B is 95 m hence

h = 95 - 70 = 25 m

L = 400 m, T = 1100 kg and w = 0.8 kg/m

c) The point B is at 95 m from the water level while point O which is lowest point on trajectory is 29.731 m down from point B. Hence clearance of point O from the water level is

= 95 - 29.731 = 65.2689 m

 

3. Factor of Safety

While calculating sag and tension in a conductor a factor of safety is always considered.

Every conductor has certain ultimate strength which it can sustain. If tension increases beyond this value, mechanical failure of conductor occurs. This ultimate strength is called breaking stress. While the normal tension T is called the working stress. The ratio of breaking stress to the working stress is defined as the factor of safety. Both breaking stress and working stress must be expressed in same units. The factor of safety is denoted as Sf and mathematically expressed as,

The stress is generally expressed in kg/m² or kg/cm² hence it must be multiplied by the conductor area to express it in kg.

 

Example 4.3.3 The towers of height 30 m and 90 m respectively support a transmission line conductor at water crossing. The horizontal distance between the towers is 560 m. The ultimate strength of the conductor is 6400 kg. Find the minimum clearance of the conductor and water and clearance mid-way between the supports. Weight of the conductor is 1.5 kg/m. Bases of towers can be considered to be at water level. Factor of safety may be taken as 4.

AU : May-04, Marks 8

Solution :

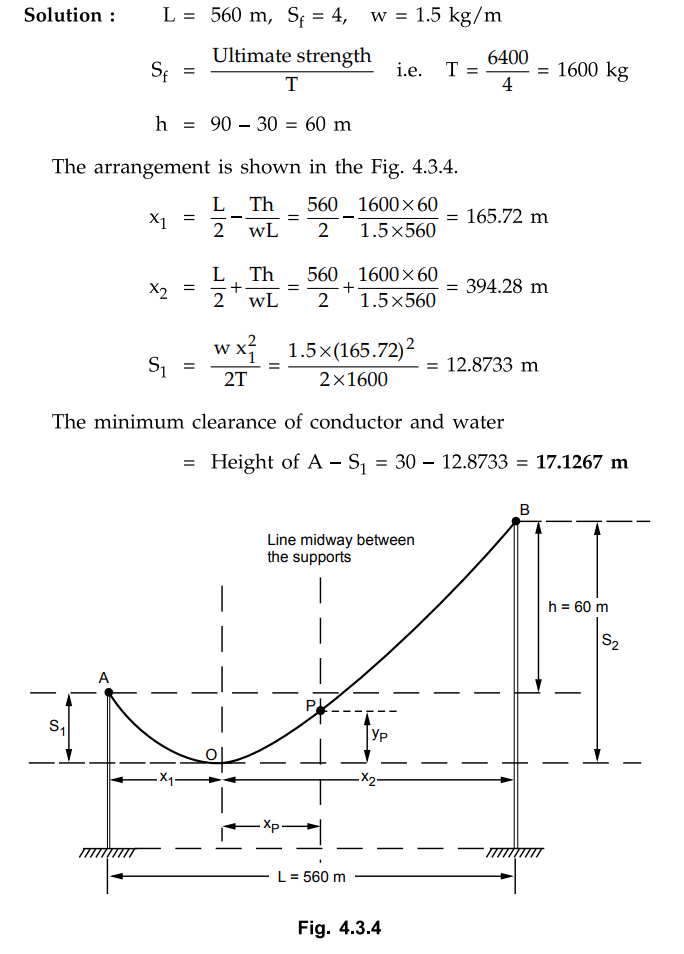
The distance of point P from the ground is the clearance midway between the supports.

The origin is point O and co-ordinates of point P are (x_p, y_p)

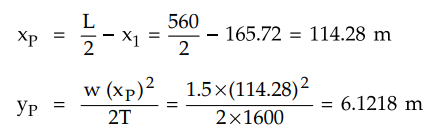
The point P is y_p distance above the origin O and the origin O is 17.1267 m above water.

Hence total clearance midway between the supports is

= Clearance of O + y_P = 17.1267 + 6.1218 = 23.2485 m

 

Example 4.3.4 An overhead line has a span of 336  m. The  line is supported at a water crossing from two towers whose heights are 33.6  m and 29 m above water level. The weight of conductor is 8.33 N/m and   tension in the conductor is not to exceed 3.34 × 10⁴N. Find i) Clearance between the lowest point on the conductor   and water ii) Horizontal distance of this point from the lower support.

Solution : L = 336 m, T = 3.34 ×  10⁴N, w = 8.33 N/m

The arrangement is shown in the Fig. 4.3.5.

h = Difference in level = 33.6 - 29 = 4.6 m

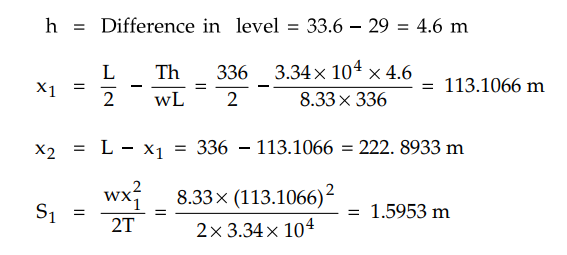
i) Clearance between the lowest point on the conductor and water is

= Height of A – S1 = 29 – 1.5953 = 27.4047m

ii) Horizontal distance of the point O from tower A = x₁ = 113.1066 m

 

Example 4.3.5 An overhead line conductor is supported by the two towers which are at 70 m height above the water level. The towers are separated from each other by horizontal distance of 300 m. The tension in the conductor is 1500 kg. Find the clearance at a point midway between the towers if size of the conductor is 0.92 cm² and density of the conductor material is 8.87 gm/cm³ .

Solution : The span L = 300 m, T = 1500 kg

Weight per metre = Area of cross-section in m² × Density in kg/m³

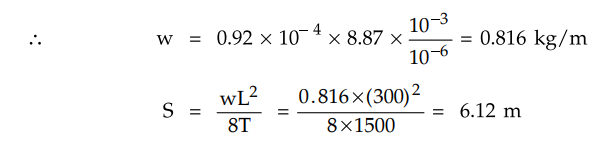
The clearance from the ground is shown in the Fig. 4.3.6.

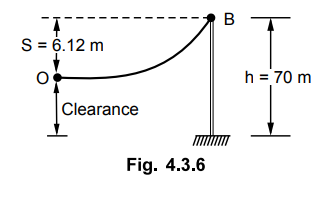
Clearance = Height h - Sag S

= 70 - 6.12

= 63.88 m 

 

Example 4.3.6 A transmission line over a hill having gradient of 1 in 10 is supported bp 40 m towers with a distance of 250 m between them. Find the clearance of the lowest point of conductor from the ground. The conductor weighs 1.5 kg/m and the working tension is 1200 kg.

Solution : The towers are on hillside having gradient 1 in 10 as shown in the Fig. 4.3.7.

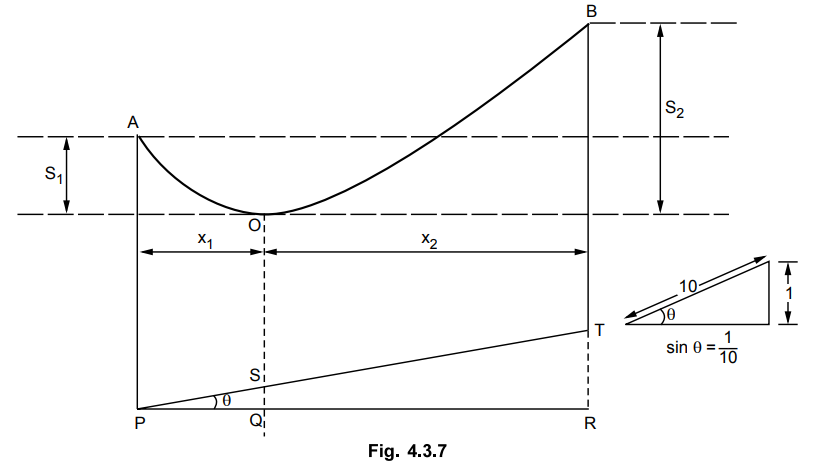
The difference in level of the supports is distance TR.

The horizontal distance between the supports is

This is the distance of lowest point of conductor from the ground.

 

Example 4.3.7 An overhead transmission line at a river crossing is supported from the two towers at heights of 25 m and 75 m above water level. The horizontal distance between the towers is 250 m. If the required clearance between the conductor and water midway between the towers is 45 m and if both the towers are on the same side of the point of maximum sag of the parabolic configuration. Find the stringing tension in the conductor. The conductor weight is 0.7 kg/m.

Solution : The arrangement is shown in the Fig. 4.3.8. It is given that both the supports are on the same side of point O which is maximum sag point.

h = 75 - 25 = 50 m

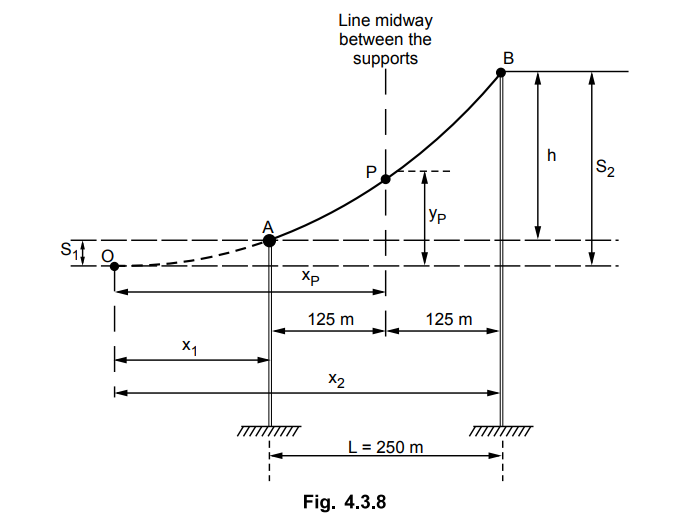
The clearance of point P which is midway between the towers from water is 45 m. Let yP be the vertical distance of P from the origin O and distance of O from the water is difference between height of tower B and sag S₂ at support B.

Clearance of P = y_P + Clearance of point O

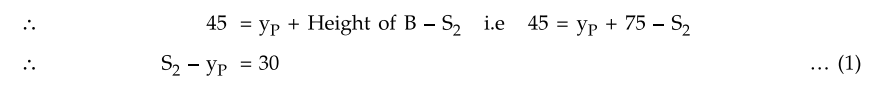
Now x₁ is negative as on the same side as that of x₂.

x₂  - x₁  = L     i.e. x₂  - x₁  = 250          ... (2)

Now as per the expressions of x₂  and x₁  derived for supports at different levels,

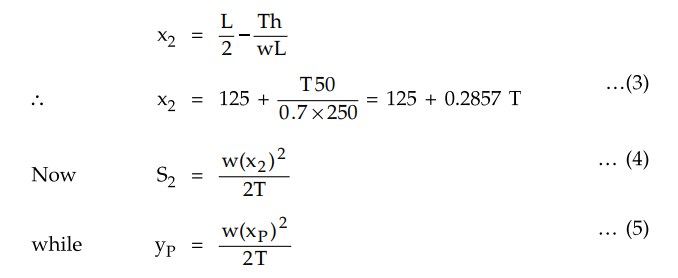
The equation (5) is obtained from parabolic nature of conductor. Substituting (4) and (5) in (1).

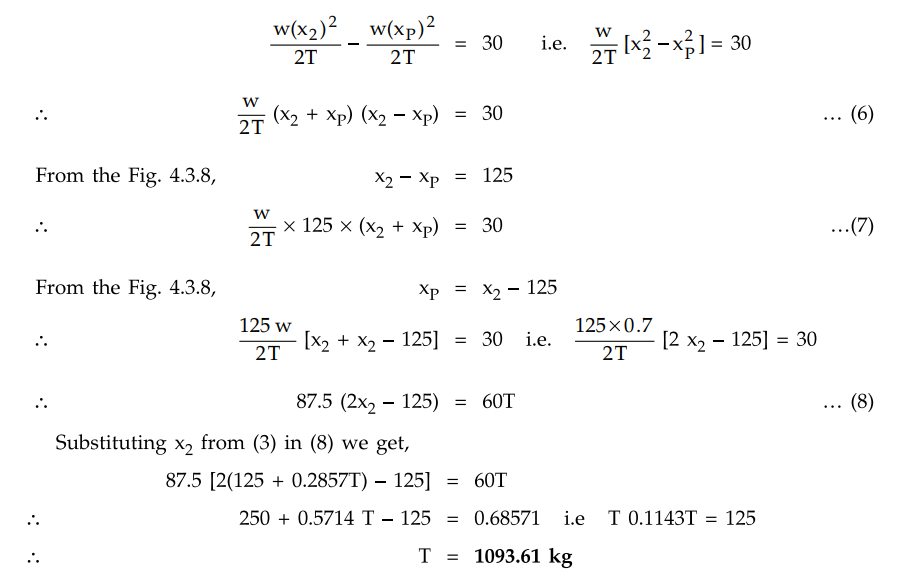
This is the stringing tension in the conductor.

 

Example 4.3.8 An OHL at a river crossing is supported from two towers of heights 30 m and 90 m above water level with the span of 300 m. The weight of the conductor is 1 kg/m and working tension is 2000 kg. Determine the clearance between the conductor and the water level midway between the towers.

Solution : Heights of towers 30 m and 90 m, L = 300 m

h = 90 - 30 = 60 m, T = 2000 kg, w = 1 kg/m.

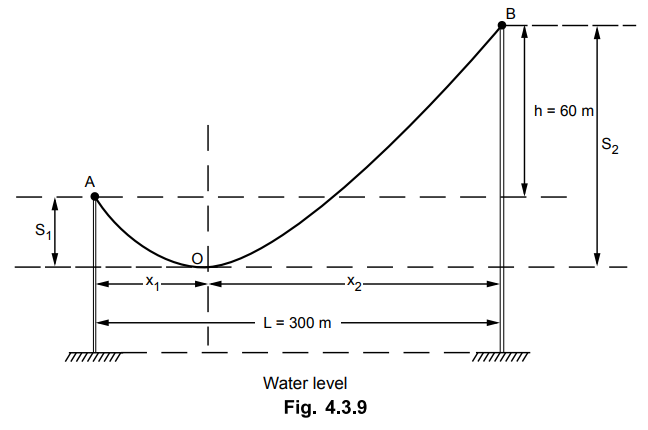
The towers and conductors is shown in the Fig. 4.3.9 where S₁ and S₂ are sags at two supports.

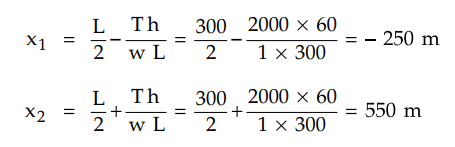
It can be seen that x1 is negative which indicates that the lowest point of the trajectory i.e. point O occurs to the left of support A. So support A is to the right of point O. So between supports A and B the lowest point of trajectory does not exist. The case is shown in the Fig. 4.3.9 (a).

Origin is O and point P is located midway between the towers, on the conductor.

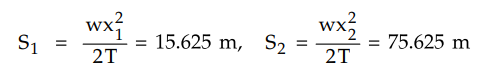
From Fig. 4.3.9 (a), x_p = x₁ +L / 2 = 250 + 150 = 400 m from O. This is horizontal distance of point P from the point O. The corresponding vertical distance of point P from the level of origin O is y p and given by,

The clearance of point O from water level

= Height of A - S₁ = 30 - 15.625 = 14.375 m

Clearance of point P i.e. point midway between the towers and the water level is,

= 14.375 + y_P = 14.375 + 40 = 54.375 m

 

Example 4.3.9 Calculate the horizontal component of tension and maximum sag for a span of 300 m if the maximum tension in the conductor be 3500 kg and weight of conductor is 700 kg/km. Determine also the location of the points on the conductor at which the sag will be half of the above value.

Solution : w = 700 kg/km = 0.7 kg/m, T = 3500 kg, L = 300 m

The tension T acts in the horizontal component hence,

Horizontal component of tension = T = 3500 kg

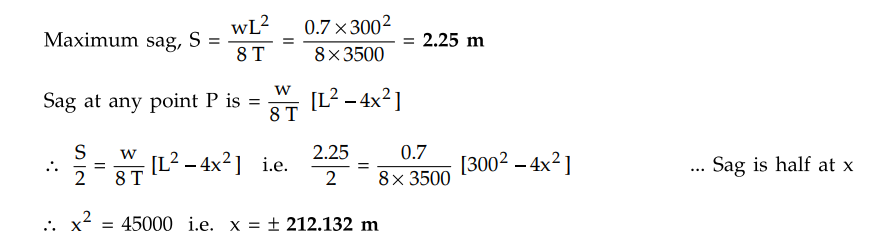
Thus sag will be half of the maximum at points which are 212.132 m away from maximum sag point, on either sides.

Review Questions

1. Derive an expression for the sag in a transmission line.

i) When the supports are at equal heights. Assume shape of overhead line is a parabola.

AU : May-11, Dec.-12, 13, 15, Marks 8

ii) When the supports are at unequal heights. Assume shape of overhead line is a parabola.

AU : May-11, Marks 8

2. A transmission line conductor at a river crossing is supported from two towers of heights 50 mts and 80 mts above water level. The horizontal distance between the towers is 500 mts. If the tension in the conductor is 3000 kgs. Find the minimum clearance between the conductor and water. Weight cf the conductor per meter is 0.844 kg.

[Ans.: 49.8103 m]

3. An overhead transmission line is supported by the two towers which are at 90 m height above the water level. The horizontal distance between the towers is 250 m. The tension in the conductor is 1490 kg. Find the clearance at a point midway between the towers if size of the conductor is 1.29 cm and density of the conductor material is 8.9gm/cm .

[Ans.: 83.98 m]

4. A transmission line over a hill side where the gradient is 1 : 20 is supported by two 20 m high towers, with a distance of 300 m between them. Find the clearance of the conductor from the ground, at the point of maximum sag. The conductor weighs 1 kg/m. The ultimate strength is 3000 kg and the factor of safety is 2.

[Ans.: 14.38 m]

5. The towers of height 30 m and 90 m respectively support a transmission line conductor at water crossing. The horizontal distance between the towers is 500 m. If the tension in the conductor is 1600 kg, find the minimum clearance of the conductor and water and also clearance midway between the supports. Weight o/ conductor is 1.5 kg/m. Bases of the towers can be considered to be at water level.

[Ans.: 23.0232 m, 30.7032 m]