Capacitance of a Single Core Cable

Capacitance of a Single Core Cable

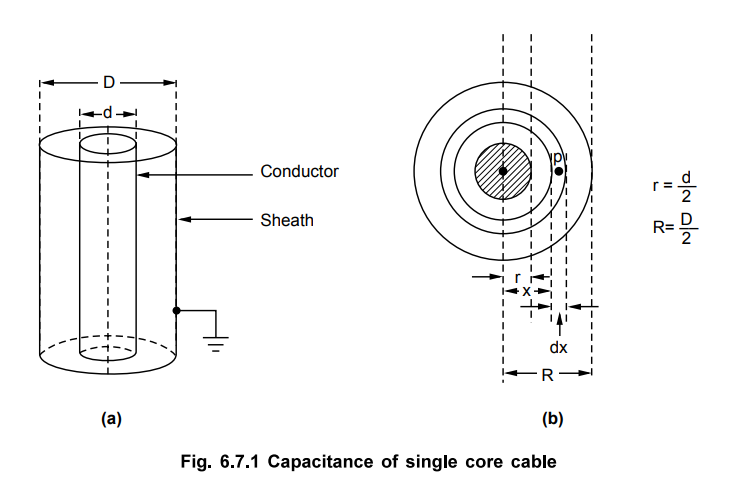
A single core cable is equivalent to two long co-axial cylinders. The inner cylinder is the conductor itself while the outer cylinder is the lead sheath. The lead sheath is always at earth potential.

Let     d = Conductor diameter and

D = Total diameter with sheath

The co-axial cylindrical form of cable and its section are shown in the Fig. 6.7.1 (a) and (b).

Let     Q = Charge per metre length of conductor in coulombs

ε = Permittivity of material between core and sheath

Now  ε = ε₀ ε_r 

where  ε₀ = Permittivity of free space = 8.854 × 10 12 F/m

and    ε_r = Relative permittivity of the medium

Consider an elementary cylinder with radius x and axial length of 1 m. The thickness of the cylinder is dx.

According to Gauss's theorem, the lines of flux emanating due to charge Q on the conductor are in radial direction and total flux lines are equal to the total charge possessed i.e. Q lines. As lines are in radial direction, the cross-sectional area through which lines pass is surface area. For a cylinder with radius x, the surface area is (2πx × axial length)m². As axial length considered is 1 m, the surface area is 2πx × m²

Flux density = Q /  Surface area        = Q / 2πx C / m²

The electric field intensity at any point P on the elementary cylinder is given by,

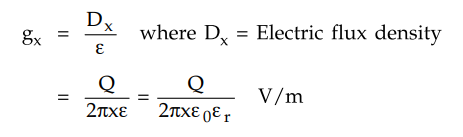
Hence the work done in moving a unit charge through a distance dx in the direction of an electric field is g_x dx.

Therefore the work done in moving a unit charge from the conductor to sheath is the potential difference between the conductor and the sheath given by,

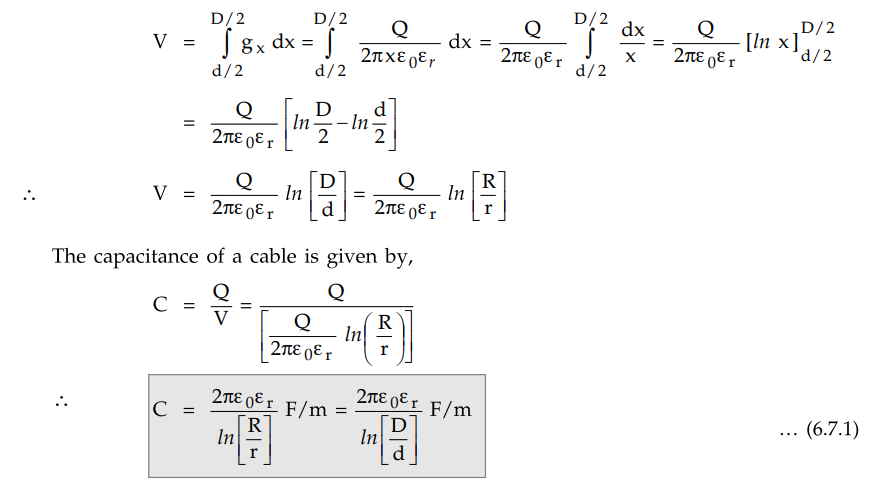
Note that as length considered is 1 m, the capacitance is F/m. If required for length l multiply C by l.

Substituting value of ε₀ ,

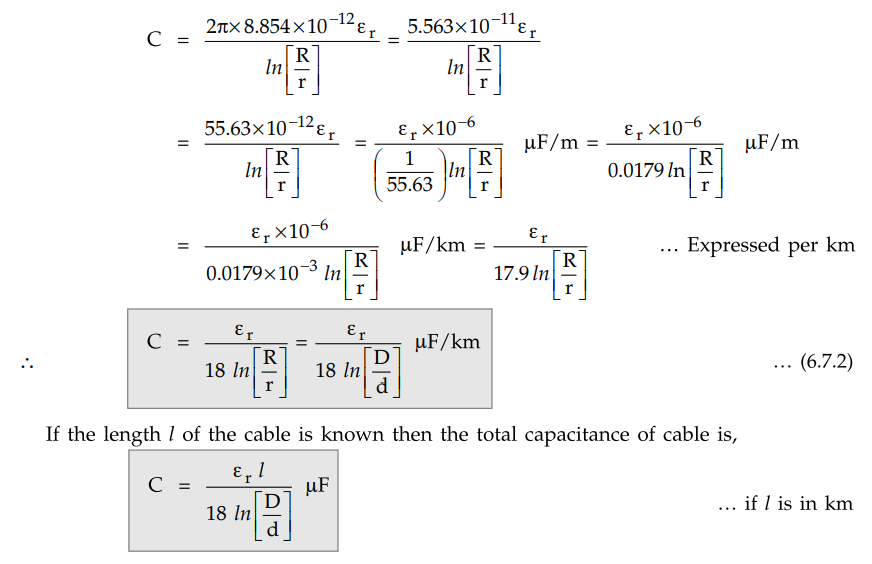
Note : To avoid the confusion of units, students can use the expression given by equation (6.7.1), to calculate capacitance while solving the problem.

Charging current : When the capacitance C of a cable is known then its reactance is given by,

X_C = 1 / ωC = 1 / 2πfC Ω

Then the charging current of the cable is given by,

I_C = V_ph / X_C where V_ph = Phase voltage between core and sheath = V_line / √3

 

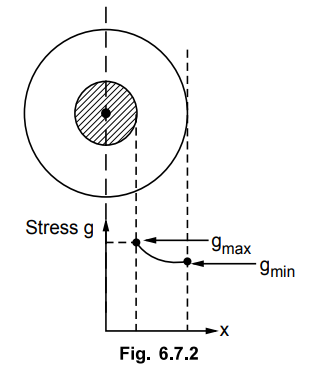
1. Stress in Insulation

The electrical stress in insulation is the electric field intensity acting at any point P in insulation.

The variation of stress in the dielectric material is shown in the Fig. 6.7.2.

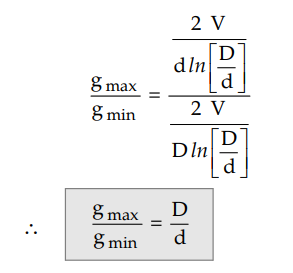
The ratio of maximum and minimum stress is,

Key Point If value of voltage used is r.m.s. we get r.m.s. values of stresses and if value of voltage used is peak, we get peak values of stresses.

 

2. Economical Core Diameter

In practice, the maximum stress value should be as low as possible. When the voltage V and sheath diameter D are fixed, the only parameter to be selected is the core diameter d. So d should be selected for which g_max value is minimum.

Key Point The core diameter must be 1/2.718 times the sheath diameter D so as to give the minimum value of g_max.

The value of minimum g_max is,

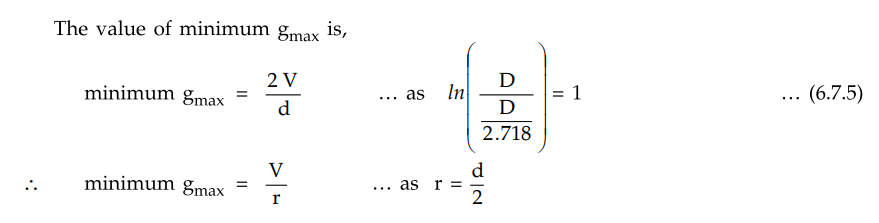
For high voltage cables, for a required gmax if d is determined by the expression (6.7.5), it gives very large values of d than required for current carrying capacity. And such extra copper required can increase the cost tremendously. Hence to increase d without the use of an extra copper following methods are used :

1. Aluminium is used instead of copper as the aluminium size is more than copper for the same current carrying capacity.

2. Using stranded copper conductors around a dummy core of jute or hemp.

3. Using stranded copper conductors around a lead tube instead of hemp.

 

Example 6.7.1 A concentric cable has a conductor diameter of 0.6 cm and the insulation thickness of 1.4 cm. If the dielectric used has relative permittivity of 5, calculate the capacitance for 1 km length of the cable.

Solution d = 0.6 cm and t = 1.4 cm

D = d + 2t

 

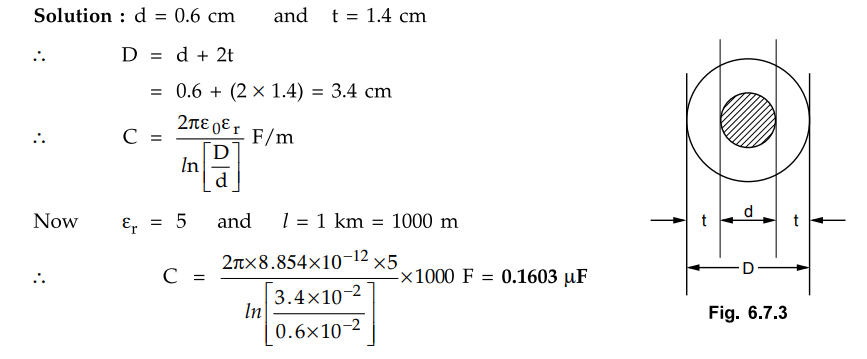
Example 6.7.2 The r.m.s. values maximum and minimum stresses in the insulation of a single core cable are 50 kV/cm and 15 kV/cm respectively. The conductor diameter is 1.8 cm. Calculate: a) Thickness of insulation b) Working voltage

Solution:

As g_max given is r.m.s., the value of working voltage is also r.m.s.

 

Example 6.7.3 Calculate the capacitance, charging current and the insulation resistance of a single core cable 33 kV, 50 Hz and 2 km long having a core diameter of 2 cm and the sheath diameter of 7 cm. The relative permittivity of the insulation is 3.5 and the resistivity of the insulation is 4.5 × 10¹⁴Ω cm.

Solution : d = 2 cm, D = 7 cm, l = 2 km, ε_r = 3.5, p = 4.5x 10¹⁴ Ω cm

Example 6.7.4 Calculate the most economical diameter of a single core cable to be used on 132 kV, 3 phase system. Find also the overall diameter of the insulation, if the peak permissible stress is not to exceed 60 kV/cm.

AU: Dec.-05, 15, Marks 8

Solution :

 

Example 6.7.5 A single core cable has a conductor of diameter 3 cm and inside diameter of lead sheath is 6 cm. If the cable is designed for operating voltage of 33 kV (line to neutral), find

i) Maximum and minimum values of electric stress.

ii) Optimal value of conductor radius for the smallest value of the maximum stress.

AU: May-06, Marks 8

 

Example 6.7.6 A 33 kV single core cable has a conductor diameter of 1 cm and a sheath of inside diameter 4 cm. Find the maximum and minimum stress in the insulation.

AU : Dec.-13, Marks 6

Solution : d = 1 cm, D = 4 cm, V]ine =33 kV (r.m.s.)

 

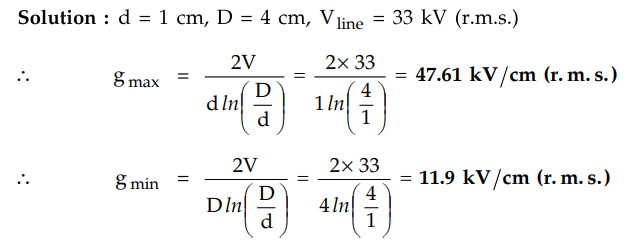
Example 6.7.7 A single core cable has a conductor diameter of 1 cm and internal sheath diameter of 1.8 cm. If impregnated paper of relative permittivity 4 is used as the insulation calculate the capacitance for 1 km length of the cable.

AU: May-18, Marks 5

Solution :

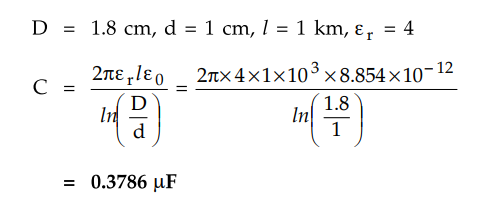
Review Questions

1. Derive an expression for the maximum and minimum dielectric stress in a single core cable and obtain the criterion for keeping the dielctric stress to a minimum value.

2. Derive the expression for the capacitance of a single core cable and give the expression for the maximum and minimum dielectric stress.

AU: May-18, Marks 8

3. A single core cable has a conductor diameter of a 1 cm and internal sheath diameter of 3 cm. If PVC of relative permittivity 5 is used as the insulation, calculate the capacitance for 1 km length of the cable.

 [Ans. : 0.253 μF]

4. Prove that the most economical conductor size in a cable is d = D / 2.718

5. Calculate the most economical diameter of a single core cable to be used on 132 kV, 3 phase system. Find also the overall diameter of the insulation if the peak permissible stress is not to exceed 60 kV/cm. 

[Ans.: 3.6 cm, 9.79 cm]

6. Calculate the capacitance and charging current of a single core cable used in 3 phase, 66 kV system. The cable is 1 km long and having a core diameter of 15 cm and impregnated paper insulation of thickness 22.5 cm. The relative permittivity of the insulation may be taken as 3.5 and supply frequency at 50 Hz.         

[Ans.: 0.1404 µF, 1.68 A]