Capacitance of Three Core Cables

Capacitance of Three Core Cables

In three core cables, capacitances play an important role because in such cables capacitances exist between the cores as well as each core and the sheath. These capacitances are dominating as the dielectric constant of the dielectric used in cables is much more than the air. The capacitances are shown in the Fig. 6.9.1. 

The core to core capacitances are denoted as C_C while core to sheath capacitances are denoted as C_S.

The core to core capacitances C_C are in delta and can be represented in the equivalent star as shown in the Fig. 6.9.2.

The impedance between core 1 and the star point, Z₁ can be obtained as,

If star point is assumed to be at earth potential and if sheath is also earthed then the capacitance of each conductor to neutral is,

C_N = C_S + C₁ = C_S + 3 C_C

If V_ph is the phase voltage then charging current per phase is,

 

1. Measurement of C_S and C_C

The total capacitance CN is not easy to calculate but by actual practical measurement Cs and Cc can be determined.

Practical measurement involves two cases :

Case 1 : The cores 2 and 3 are connected to sheath.

Thus the C_C between cores 2 and 3 and C_S between cores 2, 3 and sheath get eliminated as shown in the Fig. 6.9.3.

All the three capacitances are now in parallel across core 1 and the sheath.

The capacitance of core 1 with sheath is measured practically and denoted by C_a.

C_a = C_S + 2 C_C

Case 2 : All the three cores are bundled together.

This eliminates all the core-core capacitances. This is shown in the Fig. 6.9.5.

The capacitances C_S are in parallel between the common core and sheath.

This capacitance is practically measured and denoted as C_b.

C_b = 3 C_S ... (6.9.2)

Solving equations (6.9.1) and (6.9.2) simultaneously,

Thus both the capacitances can be determined.

 

Example 6.9.1 A 3 core, 3 phase metal sheathed cable on testing for the capacitance gave the following results :

i) Capacitance between all conductors bunched and sheath = 0.6 µF

ii) Capacitance between two conductors bunched with sheath and third conductor = 0.36 µF

With the sheath insulated find,

a) Capacitance between any two conductors

b) Capacitance to neutral

c) Charging current if cable is connected to 11 kV, 3 phase, 50 Hz system.

Solution : The methods used to measure the capacitances are described earlier.

a) To find capacitance between any two conductors Converting internal star to equivalent delta,

The equivalent circuit is shown in the Fig. 6.9.7.

Hence capacitance between any two conductors is as shown in the Fig. 6.9.8.

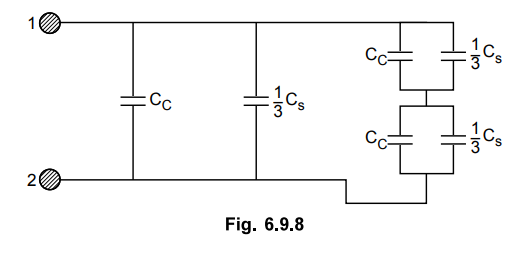
Two equal capacitances in series give equivalent 1 ( equal to half the value of each capacitance.

 

2. Capacitance of Three Core Cable

There is one empirical formula to calculate the capacitance of a three core belted cable, stated by Simon. It is applicable for the circular conductors. The formula gives the capacitance of a three core cable to neutral per phase per kilometre length of the cable. The formula is given as,

where, ε_r = Relative permittivity of the dielectric

d = Conductor diameter

t = Belt insulation thickness

T = Conductor insulation thickness

The formula can be used when the test results are not available. This gives approximate value of the capacitance. If e r is not given, it can be assumed to be 3.5. It must be remembered that all the values of d, t and T must be used in the same units while using the formula.

 

Example 6.9.2 A three core cable has core diameter of 2 cm and core to core distance of 4 cm. The dielectric material has relative permittivity of 5. Compute the capacitance of this cable per phase per km. Thickness of the conductor insulation is 1 cm and that of belt insulation is 0.5 cm.

Solution : d = 2 cm, ε_r = 5, T = 1 cm, t = 0.5 cm

Use the empirical formula as the test results are not given.

 

Example 6.9.3 A 2 km long 3 core, 3 cable has capacitance 0.5 pF/km between two conductors bunched with sheath and the third conductor. The capacitance between the conductors is also measured when bunched together and the sheath and found to be 0.75 pF/km. Determine

i) Capacitance between phases

ii) Capacitance between the conductor and the sheath

iii) Effective per phase capacitance

iv) Capacitance between two conductors connecting a third conductor to the sheath

v) Charging current if the supply voltage is 11 kV, 50 Hz.

Solution : Case i) The cores 2 and 3 are connected to sheath and core 1.

C_a = C_S + 2C_C= 0.5 µF/km

Case ii) 3 cores bunched together and sheath

iv) Capacitance between two conductors connecting a third conductor to the sheath.

 

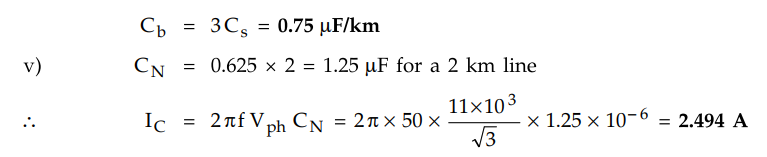
Example 6.9.4 The capacitance per kilometer of a 3 phase belted core cable is 0.2 micro farad/km between two cores with the third core connected to sheath. Calculate the kVA. The supply voltage 6.6 kV and 30 km long. 

Solution : The capacitance between two cores with third core connected to sheath is C3 = 0.2 µF/km. In such a case; one of the capacitor C_S is eliminated and this gives,

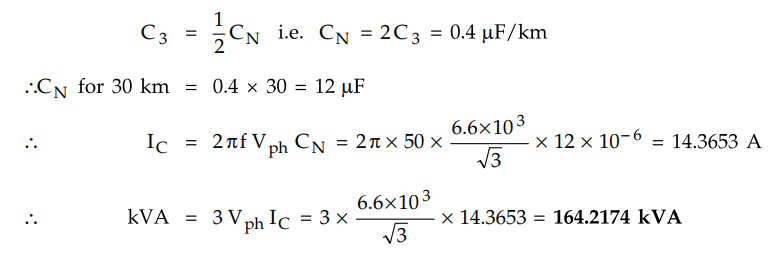
Review Questions

1. Describe an experiment to determine the capacitance of a belted 3 phase cable.

2. Derive an expression for the capacitance of a three core cable and the charging current.

3. A3 core, 3 phase metal sheathed cable gave the following results on testing for cables :

i) Capacitance between all conductors bunched and the sheath is 0.9 µF.

ii) Capacitance between two conductors bunched connected to sheath and third conductor is 0.4 µF. Calculate,

a) Capacitance between any two conductors b) The capacitance to neutral c) The charging current taken by the cable when connected to 22 kV, 3 phase, 50 Hz system.

[Ans.: 0.15 µF, 0.45 µF, 1.7956 A]