Cartesian Co-ordinate System

Cartesian Co-ordinate System

AU : May-05, Dec.-08

• This is also called rectangular co-ordinate system. This system has three co-ordinate axes represented as x, y and z which are mutually at right angles to each other. These three axes intersect at a common point called origin of the system. There are two types of such system called

1. Right handed system and 2. Left handed system.

• The right handed system means if x axis is rotated towards y axis through a smaller angle, then this rotation causes the upward movement of right handed screw in the z axis direction. This is shown in the Fig. 1.6.1 (a). In this system, if right hand is used then thumb indicates x axis, the forefinger indicates y axis and middle finger indicates z axis, when three fingers are held mutually perpendicular to each other.

• In left handed system x and y axes are interchanged compared to right handed system. This means the rotation of x axis into y axis through smaller angle causes the downward movement of right handed screw in the z axis direction. This is shown in the Fig. 1.6.1 (b).

Key Point : The right handed system is very commonly used and followed in this book.

• In cartesian co-ordinate system x = 0 plane indicates two dimensional y-z plane, y = 0 plane indicates two dimensional x-z plane and z = 0 plane indicates two dimensional x-y plane. 

1. Representing a point in rectangular co-ordinate system

• A point in rectangular co-ordinate system is located by three co-ordinates namely x, y and z co-ordinates. The point can be reached by moving from origin, the distance x in x direction then the distance y in y direction and finally the distance z in z direction. Consider a point P having co-ordinates X₁,Y₁ and Z₁ It is represented as P (x₁,y₁,z₁ )

• It can be shown as in the Fig. 1.6.2 (a) The co-ordinates X₁,y₁ and z₁ can be positive or negative. The point Q (3,-1,2) can be shown in this system as in the Fig. 1.6.2 (b).

• Another method to define a point is to consider three surfaces namely x = Constant, y = Constant and z = Constant planes. The common intersection point of these three surfaces is the point to be defined and the constants indicate the co-ordinates of that point. For example, consider point Q which is intersection of three planes namely x = 3 plane, y = -1 plane and z = 2 plane. The planes x = Constant, y = Constant and z = Constant are shown in the Fig. 1.6.3. (Refer Fig. 1.6.3 ). The constants may be positive or negative.

2. Base Vectors

• The base vectors are the unit vectors which are strictly oriented along the directions of the co-ordinate axes of the given co-ordinate system.

•  Thus for cartesian co-ordinate system, the three base vectors are the unit vectors oriented in x, y and z axis of the system. So 

 are the base vectors of cartesian co-ordinate system. These are shown in the Fig. 1.6.4.

 

• So any point on x-axis having co-ordinates (x₁,0,0) can be represented by a vector joining origin to this point and denoted as x₁ 

• The base vectors are very important in representing a vector in terms of its components, along the three co-ordinate axes.

 

3. Position and Distance Vectors

• Consider a point P (x₁,y₁,z₁) in cartesian co-ordinate system as shown in the Fig. 1.6.5. Then the position vector of point P is represented by the distance of point P from the origin, directed from origin to point P. This is also called radius vector. This is also shown in the Fig. 1.6.5.

• Now the three components of this position vector  are three vectors oriented along the three co-ordinate axes with the magnitudes x₁,y₁ and z₁.Thus the position vector of point P can be represented as,

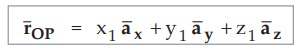....(1.6.1)

• The magnitude of this vector interms of three mutually perpendicular components is given by,

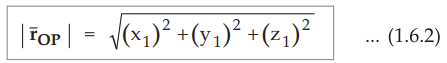Thus if point P has co-ordinates (1,2,3) then its position vector is,

• Many a times the position vector is denoted by the vector representing that point itself i.e. for point P the position vector is  for point Q it is  and so on. The same method is used hereafter in this book. Note the difference between a point and a position vector.

• Now consider the two points in a cartesian co-ordinate system, P and Q with the co-ordinates (x₁,y₁,z₁) and (x₂,y₂,z₂) respectively. The points are shown in the Fig. 1.6.6.

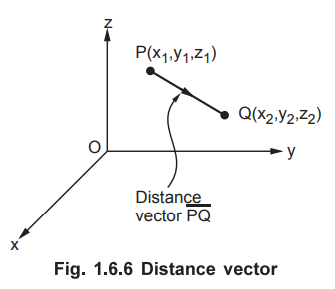
The individual position vectors of the points are,

• Then the distance or the displacement from P to Q is represented by a distance vector  and is given by,

• This is also called separation vector.

• The magnitude of this vector is given by,

• This is nothing but the length of the vector PQ. The equation (1.6.4) is called distance formula which gives the distance between the two points representing tips of the vectors.

• Using the basic concept of unit vector, we can find unit vector along the direction PQ as,

• Once the position vectors are known then various mathematical operations can be easily performed interms of the components of the various vectors.

• Let us summarize procedure to obtain distance vector and unit vector.

Step 1 : Identify the direction of distance vector i.e. starting point (x₁,y₁,z₁) and terminating point (x₂,y₂,z₂)

Step 2 : Subtract the respective co-ordinates of starting point from terminating point. These are three components of distance vector i.e. 

Step 3 : Adding the three components distance vector can be obtained.   

Step 4 : Calculate the magnitude of the distance vector using equation (1.6.4).  

Step 5 : Unit vector along the distance vector can be obtained by using equation (1.6.5).     

 

Ex. 1.6.1  Two points A (2, 2,1) and B (3, -4, 2) are given in the cartesian system. Obtain the vector from A to B and a unit vector directed from A to B.

Sol. : The starting point is A and terminating point is B.

• It can be cross checked that magnitude of this unit vector is unity i.e.

√(0.1622)² + (-0.9733)² + (0.1622)² = 1

 

4. Differential Elements in Cartesian Co-ordinate System

• Consider a point P (x, y, z) in the rectangular co-ordinate system. Let us increase each co-ordinate by a differential amount. A new point P' will be obtained having co-ordinates (x + dx, y + dy, z + dz).

Thus, dx = Differential length in x direction

dy = Differential length in y direction

dz = Differential length in z direction

• Hence differential vector length also called elementary vector length can be represented as,

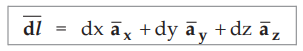....(1.6.6)

• This is the vector joining original point P to new point P'.

• Now point P is the intersection of three planes while point P' is the intersection of three new planes which are slightly displaced from original three planes. These six planes together define a differential volume which is a rectangular parallelepiped as shown in the Fig. 1.6.7. The diagonal of this parallelepiped is the differential vector length.

• The distance of P' from P is given by magnitude of the differential vector length,

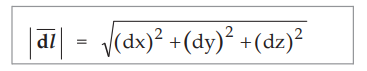 ....(1.6.7)

• Hence the differential volume of the rectangular parallelepiped is given by,

dv = dx dy dz .....(1.6.8)

• Note that  is a vector but dv is a scalar.

• Let us define differential surface areas. The differential surface element  is represented as,

 .....(1.6.9)

where dS = Differential surface area of the element

 = Unit vector normal to the surface dS

• Thus various differential surface elements in cartesian co-ordinate system are shown in the Fig. 1.6.8.

• The vector representation of these elements is given as,

• The differential elements play very important role in the study of engineering electromagnetics.

 

Ex. 1.6.2 Find the unit vector directed towards the point (x₁ ,y₁,z₁ ) from an arbitral point in the plane y = -5 .

Sol. : The plane y = - 5 is parallel to xz plane as shown in the Fig. 1.6.9.

• The co-ordinates of point P are (x, - 5, z) as y = - 5 is constant. While Q is arbitrary point having co-ordinates (x₁,y₁,z₁). To find unit vector along the direction PQ.

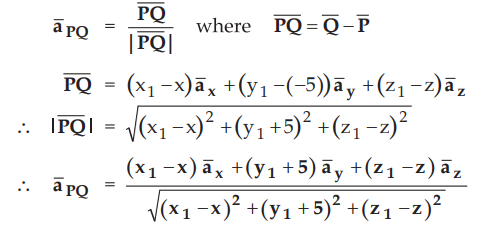
Examples for Practice

Ex. 1.6.3 : 

 

Ex. 1.6.4 : Obtain the unit vector in the direction from the origin towards the point P (3, -3,-2).

Review Question

1. Discuss the cartesian co-ordinate system used to represent field vectors. AU : May-05, Dec.-08