Central limit theorem: Example Solved Problems

Example 2.5.a(1)

The lifetime of a certain brand of an electric bulb may be considered as a RV with mean 1200 h and standard deviation 250 h. Find the probability, using central limit theorem, that the average lifetime of 60 bulbs exceeds 1250 h. or [AU N/D 2008] [AU N/D 2006] [A.U Trichy M/J 2011] [A.U N/D 2013]

[A.U N/D 2018 R-17 PS]

Solution :

Given: (1) μ = E [X] = 1200

(2) σ = S. d. [X] = 250

(3) n = 60

(4)   = mean life time of 60 bulbs

If the average of random variables follows Normal distribution, then

 

Example 2.5.a (2)

A random sample of size 100 is taken from a population whose mean is 60 and the variance is 400. Using CLT, with what probability can we assert that the mean of the sample will not differ from μ = 60 by more than 4? [AU A/M 2003, Trichy A/M 2010] [A.U A/M 2010]

Solution:

Given:

 

Example 2.5.a(3)

[A.U N/D 2013]

A distribution with unknown mean u has variance equal to 1.5. Use central limit theorem to find how large a sample should be taken from the distribution in order that the probability will be atleast 0.95 that the sample mean will be within 0.5 of the population mean. [A.U. N/D 2004] [A.U A/M 2003]

Solution :

TYPE 2. If the discrete random variables follows normal distribution, then  follows N (µ, ɑ) by CLT.

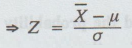
Example 2.5.b(1)

A coin is tossed 10 times. What is the probability of getting 3 or 4 or 5 heads. Use central limit theorem. [AU N/D 2009] [A.U CBT M/J 2010] [A.U N/D 2003]

Solution:

Given:

To approximate the discrete probability distribution to continuous probability distribution add 0.5 to the upperbound and subtract 0.5 from the lower bound.

 

Example 2.5.b (2)

A coin is tossed 300 times found the probability that heads will appear more than 140 times and less than 150 times.

Solution: Given:

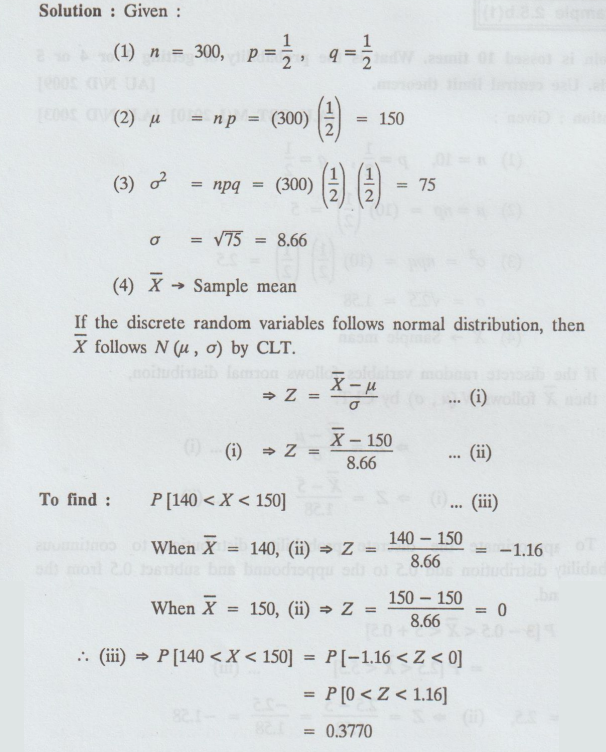
TYPE 3. If the sum of random variables follows Normal distribution, then S_n follows N (n µ, σ√n) by CLT

⇒ Z = S_n – n µ / σ√n

 

Example 2.5.c(1)

If X₁, X₂ ... X_n are Poisson variates with parameter λ = 2, use the central limit theorem to estimate P (120 ≤  S_n ≤ 160), where

S_n = X₁ + X₂ + … + X_n and n = 75.

[AU N/D 2009, N/D 2010] [A.U M/J 2012]

Solution: Given:

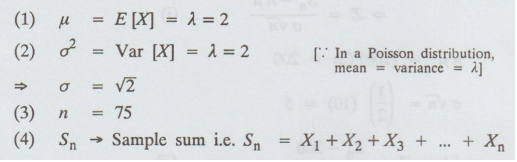
If the sum of random variables follows Normal distribution, then Sn follows N (n µ, σ √n) by CLT

 

Example 2.5.c(2)

Let X₁, X₂ …, X₁₀₀ be independent and identically distributed RVS with mean μ = 2 and σ² = 1/4.

Find P(192 < X₁ + X₂+ ... + X₁₀₀ < 210)

[A.U N/D 2012]

Solution: Given:

(1) µ = 2

(2) σ² = 1/4 ⇒ σ = 1/2

(3) n = 100

(4) S_n → Sample sum

i.e. S_n = X₁ + X₂ + ... + X₁₀₀

If the sum of random variables follows Normal distribution, then S_n follows N (nµ, σ√n) by CLT

Example 2.5.c(3)

The burning time of a certain type of lamp is an exponential random variable with mean 30 hrs. What is the probability that 144 of these lamps will provide a total of more than 4500 hrs of burning time?

 [A.U Trichy M/J 2011]

Solution:

Given:

(1) µ = 30

(2) σ² = (30) ² [In an exponential distribution variance = (mean)²]

⇒ σ = 30

(3) n = 144

(4) S_n → Sample sum

i.e. S_n = X₁ + X₂ + ... +  X₁₄₄

If the sum of random variables follows Normal distribution, then Sn follows N (nu, σ√n) by CLT

 

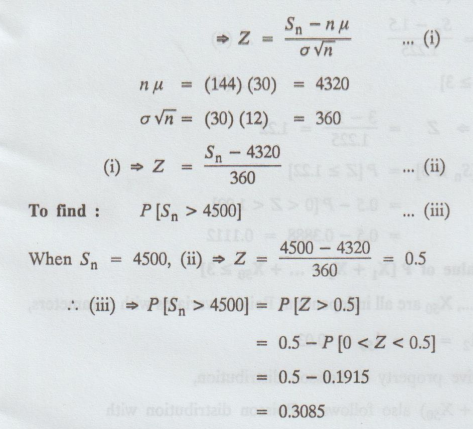
Example 2.5.c(4)

If X_i, i = 1, 2, ..., 50 are independent random variables each having a poisson distribution with parameter λ = 0.03 and S_n = X₁ + X₂ + ... + X_n evaluate P (S_n ≥ 3) using CLT. Compare your answer with the exact value of the probability.

Solution: Given:

Example 2.5.c(5)

The resistors r₁, r₂, r₃ and r₄ are independent random variables and is uniform in the interval (450, 550). Using the central limit theorem, find P (1900 ≤ r₁ + r₂ + r₃ ≤ 2100)

Solution :

Given: (a, b) = (450, 550)

(1) µ = a + b / 2

 = 450 + 550 / 2

= 500

In Mean uniform distribution

Mean = a + b / 2

Variance = (b – a)² / 12

(2) σ² = (b – a)² / 12 = (550 – 450)² / 12 = (100) ² / 12

σ = 100/√12 = 28.87

(3) n = 4, √n = 2

(4) S_n → Sample sum; S_n = r₁ + r₂ + r₃ + r₄

If the sum of random variables follows Normal distribution, then S_n follows N (nµ, σ √n) by CLT

 

Example 2.5.c(6)

If V_i, i = 1, 2, 3, ... 20 are independent noise voltages received from 'adder' and V is the sum of the voltages received, find the probability that the total incoming voltage V exceeds 105, using CLT. Assume that each of the random variables V_i is uniformly distributed over (0, 10)

Solution: Given: (a, b) = (0, 10)

 

Example 2.5.c(7)

Suppose that orders at a restaurent are identically independent random variables with mean = 8 and standard deviation σ = 2.

Estimates

(a) The probability that first 100 customers spend a total of more than 840

(b) P [780 < X₁ + X₂ + ... + X₁₀₀ < 820]

[A.U. A/M 2008]

Solution:

Given: (1) μ = 8;

(2) σ = 2

(3) n = 100;

(4) S_n → Sample sum

i.e. S_n = X₁ + X₂  + ... + X₁₀₀

If the sum of random variables follows Normal distribution, then S_n follows N (nµ, o √n) by CLT