Classification of Amplifiers

Classification of Amplifiers

AU : Dec.-03, 04, May-05

• Based on the magnitudes of the input and output impedances of an amplifier relative to the source and load impedances, respectively, we can classify amplifiers into four broad categories : Voltage, current, transconductance and transresistance amplifiers.

1. Voltage Amplifier

• Fig. 9.2.1 shows a Thevenin's equivalent circuit of an amplifier.

• If the amplifier input resistance R_i is large compared with the source resistance R_s then

V_i ≈ V_s

• If the external load resistance RL is large compared with the output resistance Ro of the amplifier, then v_o ≈ A_v V_i ≈ A_v V_s (where A_v = Voltage gain).

• Such amplifier circuit provides a voltage output proportional to the voltage input, and the proportionality factor does not depend on the magnitudes of the source and load resistances. Hence, this amplifier is called voltage amplifier.

• An ideal voltage amplifier must have infinite input resistance Ri and zero output resistance Ro. For practical voltage amplifier we must have R_i >> R_s and R_L >> R_o

2. Current Amplifier

• Fig. 9.2.2 shows Norton's equivalent circuit of a current amplifier.

• If amplifier input resistance R_i → 0, then I_i ≈ I_s .

• If amplifier output resistance R_o → 0 then I_L = A_I I_i (where A_i = Current gain).

• Such amplifier provides a current output proportional to the input current, and the proportionality factor is independent on source and  load resistances. This amplifier is called current amplifier.

• An ideal current amplifier must have zero input resistance R_i and infinite output resistance R _o.

• For practical current amplifier we must have

R _i << R_s and R_o >> R_L

3. Transconductance Amplifier

• Fig. 9.2.3 shows a transconductance amplifier with a Thevenin’s equivalent in its input circuit and Norton’s equivalent in its output circuit.

• In this amplifier, an output current is proportional to the input signal voltage and the proportionality factor is independent of the magnitudes of the source and load resistances.

• Ideally, this amplifier must have an infinite input resistance Ri and infinite output resistance Ro.

• For practical transconductance amplifier we must have Ri >> Rs and Ro >> RL. Since Ri >> Rs, Vi ≈ Vs and since Ro >> RL, IL = GmVi.

I_L = G_mV_s

where Gm = IL / Vs is the transfer or mutual conductance.

4. Transresistance Amplifier

• Fig. 9.2.4 shows a transresistance amplifier Norton’s equivalent in its input circuit and a Thevenin’s equivalent in its output circuit.

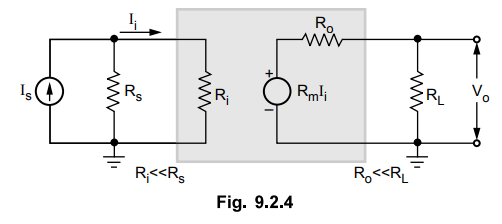
• In this amplifier an output voltage is proportional to the input signal current and the proportionality factor is independent on the source and load resistances.

• Ideally, this amplifier must have zero input resistance Ri and zero output resistance Ro.

• For practical transresistance amplifier we must have R_i << R_s and R_o << R_L. Since R_i << R_L,  Since R₁ << Rs, I_i = Is and since Ro << R_L, V_o = R_m I_j.

where Rm =  Vo / Is is the transfer or mutual resistance Is

Review Questions

1. Draw the equivalent circuit of a voltage amplifier.

AU : ECE : Dec.-04, Marks 2

2. Draw the equivalent circuit of a current amplifier.

3. Draw the equivalent circuit of transconductance amplifier.

4. Draw the equivalent circuit of transresistance amplifier.