Code Conversion

Code Conversion

This technique allows programmer to translate a number represented using one coding system to another. For example, when we accept any number from the keyboard it is in ASCII code. But for processing, we have to convert this number in its hex equivalent. The code conversion involves some basic conversions such as

• BCD to binary conversion

• Binary to BCD conversion

• BCD to seven segment code conversion

• Binary to ASCII conversion and

• ASCII to binary conversion.

 

1. BCD to Binary Conversion

We are more familiar with the decimal number system. But the microprocessor understands the binary/hex number system. To convert BCD number into its binary equivalent we have to use the principle of positional weighting in a given number.

For example : 67 = 6 × 0AH + 7

= 3CH + 7 = 43H

To perform above operation it is necessary to separate an 8-bit packed BCD number into two 4-bit unpacked BCD digits : BCD₁ and BCD₂ and then convert each digit into its binary value according to its positions. Finally, add both binary numbers to obtain the binary equivalent of the BCD number. Let us see the program for 2-digit BCD to binary conversion.

 

Lab Experiment 3.3.1 : 2-Digit BCD to binary conversion.

Statement : Convert a 2-digit BCD number stored at memory address 2200H into its binary equivalent number and store the result in a memory location 2300H.

Sample problem :

(2200H) = 67H

(2300H) = 6 × 0AH + 7 = 3CH + 7 = 43H

Source program :

LDA 2200H ; Get the BCD number

MOV B, A ; Save it

ANI 0FH ; Mask most significant four bits

MOV C, A ; Save unpacked BCD1 in C register

MOV A, B ; Get BCD again

ANI F0H ; Mask least significant four bits

RRC ; Convert most significant four

RRC ; bits into unpacked BCD2

RRC ;

RRC ;

MOV B, A ; Save unpacked BCD2 in B register

XRA A ; Clear accumulator (sum = 0)

MVI D , 0AH ; Set D as a multiplier of 10

SUM : ADD D ; Add 10 until (B) = 0

DCR B ; Decrement BCD2 by one

JNZ SUM ; Is multiplication complete ?

if not, go back and add again

ADD C ; Add BCD1

STA 2300H ; Store the result

HLT ; Terminate program execution

 

2. Binary to BCD Conversion

We know that microprocessor processes data in the binary form. But when it is displayed, it is in the BCD form. In this case we need binary to BCD conversion of data. The conversion of binary to BCD is performed by dividing the number by the power of ten.

For example, assume the binary number as

0111 1011 (7BH) = 123₁₀

TECHNICAL PUBLICATIONS - An up thrust for knowledge

To represent the number in BCD requires twelve bits or three BCD digits as shown below

123₁₀ = 0001    0010      0011

            Digit₂     digit₁     digit₀

The conversion can be performed as follows

Step 1 : If the number is equal to or greater than 100, divide number by 100 (i.e. subtract 100 repeatedly until the remainder is less than 100). The quotient gives the most significant digit, digit 2 of the BCD number. If number is less than 100 go to step 2.

Step 2 : If the number i.e. remainder of first division is equal to or greater than 10 divide number by 10 repeatedly until the remainder is less than 10. The quotient gives the digit 1. If number is less than 10, go to step 3.

Step 3 : The remainder from step 2 gives the digit 3.

Let us see the program for binary to BCD conversion.

 

Lab Experiment 3.3.2 : Binary to BCD conversion.

Statement : Write a main program and a conversion subroutine to convert the binary number stored at 6000H into its equivalent BCD number. Store the result from memory location 6100H.

Sample problem : (6000)H = 8AH

Source program :

LXI SP, 27FFH ; Initialize stack pointer

LDA 6000H ; Get the binary number in accumulator

CALL BIN TO BCD ; Call subroutine BIN TO BCD

HLT ; Terminate program execution

Subroutine to convert binary number into its equivalent

BCD number

BIN TO BCD :

PUSH B ; Save BC register pair contents

PUSH D ; Save DE register

; pair contents

MVI B, 64H ; Load divisor

; decimal 100 in B

; register

MVI C, 0AH ; Load divisor

; register

MVI D, 00H ; Initialize Digit 1

MVI E, 00H ; Initialize Digit 2

STEP1 : CMP B ; Check if number

; < Decimal 100

JC STEP 2 ; If yes go to step 2

SUB B ; Subtract decimal 100

INR E ; Update quotient

JMP STEP1 ; Go to step 1

STEP 2: CMP C ; Check if number

; < Decimal 10

JC STEP 3 ; If yes go to step 3

SUB C ; Subtract decimal 10

INR D ; Update quotient

JMP STEP 2 ; Continue division

; by 10

STEP3: STA 6100H ; Store Digit 0

MOV A, D ; Get Digit 1

STA 6101H ; Store Digit 1

MOV A, E ; Get Digit 2

STA 6102H ; Store Digit 2

POP D ; Restore DE register

; pair contents

POP B ; Restore BC register

; pair contents

RET ; Return to main

; program

 

3. BCD to Seven Segment Conversion

Many times 7-segment LED display is used to display the results or parameters in the microprocessor system. In such cases we have to convert the result or parameter in 7-segment code. This conversion can be done using look-up technique. In the look-up table the codes of the digits (0-9) to be displayed are stored sequentially in the memory. The conversion program locates the code of a digit based on its BCD digit. Let us see the program for BCD to common cathode 7-segment code conversion.

 

 Lab Experiment 3.3.3 : Find the 7-segment codes for given numbers.

Statement : Find the 7-segment codes for given 5 numbers from memory location 6000H and store the result from memory location 7000H.

Source program :

LXI H, 6200H ; Initialize lookup table pointer

LXI D, 6000H ; Initialize source memory pointer

LXI B, 7000H ; Initialize destination memory pointer

BACK : LDAX D ; Get the number

MOV L, A ; A point to the 7-segment code

MOV A, M ; Get the 7-segment code

STAX B ; Store the result at destination memory location

INX D ; Increment source memory pointer

INX B ; Increment destination memory pointer

MOV A, C ;

CPI 05H ; Check for last number

JNZ BACK ; If not repeat

HLT  ; End of program

Flowchart :

 

Lab Experiment 3.3.4 : Find the square of given number.

Statement : Find the square of the given numbers from memory location 6100H and store the result from memory location 7000H.

Source program :

LXI H.6200H       ; Initialize lookup table pointer

LXI D.6100H       ; Initialize source memory pointer

LXI B.7000H       ; Initialize destination memory pointer

BACK : LDAX D ; Get the number

MOV L, A  ; A point to the square

MOV A, M ; Get the square

STAXB      ; Store the result at destination memory location

INXD          ; Increment source memory pointer

INXB          ; Increment destination memory pointer

MOV A, C 

CPI 05H     ; Check for last number

JNZ BACK ; If not repeat

HLT  ; End of program

Flowchart :

 

4. Binary to ASCII Code Conversion

The ASCII Code (American Standard Code for Information Interchange) is commonly used for communication. In such cases we need to convert binary number to its ASCII equivalent. It is a seven bit code. In this code number 0 through 9 are represented as 30 through 39 respectively and letters A through Z are represented as 41H through 5AH. Therefore, by adding 30H we can convert number into its ASCII equivalent and by adding 37H we can convert letter to its ASCII equivalent. Let us see the program for binary to ASCII code conversion.

 

Lab Experiment 3.3.5 : Find the ASCII character.

Statement : Write an assembly language program to convert the contents of the five memory locations starting from 2000H into an ASCII character. Place the result in another five memory locations starting from 2200H.

Flowchart :

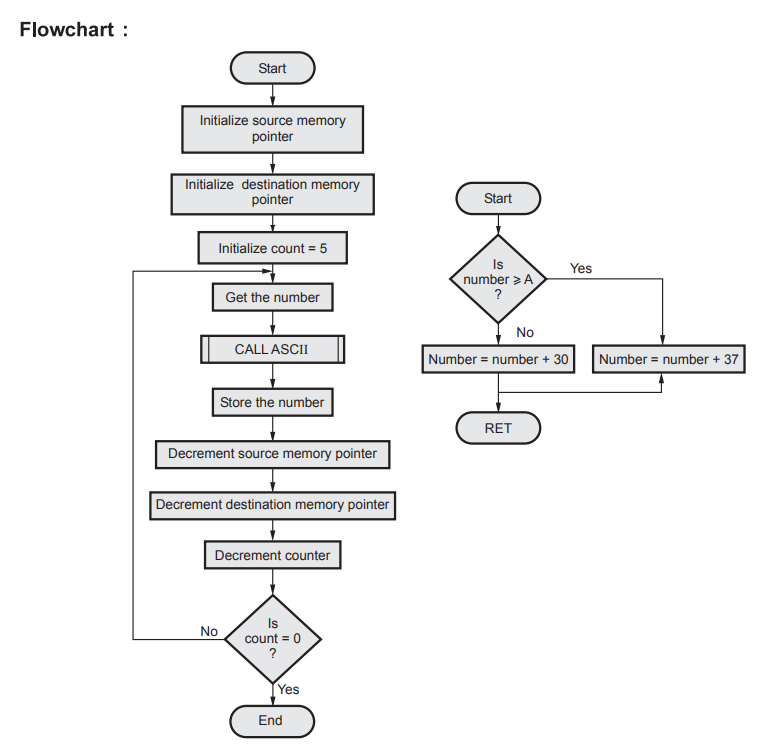
Sample problem :

(2000H) = 1

(2001H) = 2

(2002H) = 9

(2003H) = A

(2004H) = B

Result

(2200H) = 31

(2201H) = 32

(2202H) = 39

(2203H) = 41

(2204H) = 42

Subroutine documentation :

Subroutine 'ASCII' converts a hexadecimal digit to ASCII.

Passing parameter : The digit is passed using accumulator.

Return value : In the accumulator.

Register used : Accumulator.

Stack used  : From 27FEH to 27FDH

Source program :        

LXI SP, 27FFH ; Initialize stack pointer

LXI H, 2000H ; Source memory pointer

LXI D, 2200H ; Destination memory pointer

MVI C, 05H ; Initialize the counter

BACK : MOV A, M ; Get the number

CALL ASCII ; Call subroutine ASCII

STAXD ; Store result

INX H  ; Increment source memory pointer

INX D ; Increment destination memory pointer

DCR C ; Decrement count by 1

JNZ BACK ; if not zero, repeat

HLT ; Stop program execution subroutine ASCII

ASCII : CPI, 0AH          ; Check if number is 0AH

JNC NEXT ; If yes goto next otherwise continue

ADI 30H ;  

JMP LAST

NEXT : ADI 37H

LAST : RET ; Return to main program

 

5. ASCII Code to Binary Conversion

It is exactly reverse process to binary to ASCII conversion. Here, if ASCII code is less than 3AH then 30H is subtracted to get the binary equivalent and if it is in between 41H and 5AH then 37H is subtracted to get the binary equivalent of letter (A-F).

Review Questions

1. Why do we need look-up table?

2. List the common code conversions required in the microprocessor systems.

3. Explain BCD to Binary code conversion technique and write 8085 assembly language program for the same.

4. Explain Binary to BCD code conversion technique and write 8085 assembly language program for the same.

5. Explain BCD to Seven segment code conversion technique and write 8085 assembly language program for the same.

6. Explain Binary to ASCII code conversion technique and write 8085 assembly language program for the same.

7. Explain ASCII to Binary code conversion technique and write 8085 assembly language program for the same.

8. Write an 8085 Assembly program to convert a Hexadecimal Number to ASCII code.