Combination of conductively connected mutually coupled coils

COMBINATION OF CONDUCTIVELY CONNECTED MUTUALLY COUPLED COILS

Consider two coils of self inductances L₁ and L₂. Let M be the mutual inductance between them. These two coils can be connected in the following two ways:

1. Series connection,

2. Parallel connection

Again, series connection can be (a) series aiding or cumulative and (b) series opposition or differential. Similarly, the parallel connection can be (a) parallel aiding or cumulative and (b) parallel opposition or differential.

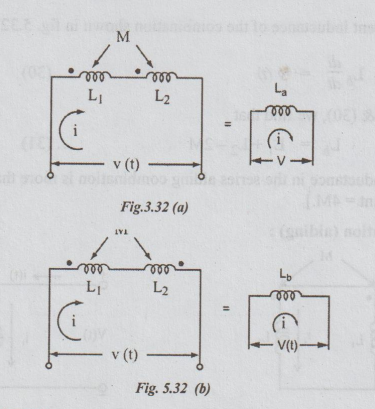
1. (a) Series connection (aiding)

Refer fig. 5.32 (a), the current is entering both the coils at the dotted terminal. So, it is called series aiding combination. For this circuit, we can write that

Let L_ɑ be the equivalent inductance of the combination shown in fig. 5.25 (a),

Then L_ɑ × di / dt = v (t) ... (27)

From equations (26) & (27), we can obtain that,

L_ɑ = L₁ + L₂ + 2M  ... (28)

(b) Series Opposition: (bucking)

Refer fig.5.32 (b), the current is entering first coil at dotted terminal and leaving the other coil at dotted terminal. So the mesh equation for this circuit is

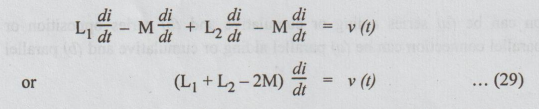
Let L be the equivalent inductance of the combination shown in fig. 5.32 (b),

Then L_b di/dt  = v (t) ... (30)

From equations (29) & (30), we find that

L_b = L₁ + L₂ – 2M … (31)

 [Note: Equivalent inductance in the series aiding combination is more than that in series opposing combination by an amount = 4M.]

2. (a) Parallel Combination (aiding):

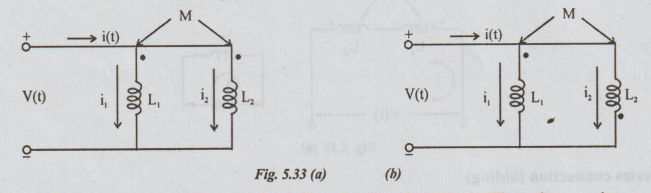
Here, both the currents i, and i2 enter the coils at the dotted terminals. Then, the equations are

L_i di₁ / dt + di₂ / dt = v (t) ... (32)

and  M di₁ / dt + L₂  di₂ / dt = v (t) ... (33)

Assume that the excitations are sinusoidal for convenience. Then, the above equations can be written as

jωL₁I₁ + jωMI₂ = V  … (34)

and jωMI₁ + jωL₂I₂ = V  ... (35)

Solving above equations for I₁ and I₂ , we get

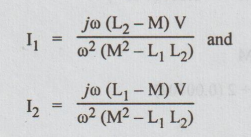
Therefore, the total current I = I₁+ I₂

I = jω (L₁ + L₂ - 2M) V / ω²(M² - L₁ L₂)

Therefore, the input impedance = V / I

ω²(M² - L₁ L₂) / jω (L₁ + L₂ - 2M) = jω (L₁ L₂ – M²) / jω (L₁ + L₂ - 2M) … (36)

Let L_a be the equivalent of the combination of inductances then

V / I = jω (L_ɑ) … (37)

From equations (36) & (37), we write that

Lɑ = L₁ L₂ – M² / L₁ + L₂ + 2M … (39)

 [Note: On observing equations (38) and (39), we can conclude that the equivalent inductance in the parallel aiding is more than that in parallel opposition. It is because the denominator of equation (38) is less than that of equation (39)]