Probability and complex function: Unit IV: Complex integration
Complex integration
Line integral, Cauchy's integral theorem
Its value depends upon the path (curve) of integration. But, the value of integral from a to b remains the same, if the different curves from a to b are regular curves.
UNIT - IV
COMPLEX
INTEGRATION
Line
integral - Cauchy's integral theorem - Cauchy's integral formula - Taylor's and
Laurent's series - Singularities - Residues - Residue theorem Application of
residue theorem for evaluation of real integrals - Use of circular contour and
semicircular contour.
Line integral - Cauchy's integral theorem - Cauchy's integral formula
In
case of real variable, the path of integration of 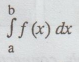 is always along
the x-axis, from x = a to x = b. But, in case of a complex function f(z) the
path of the definite integral
is always along
the x-axis, from x = a to x = b. But, in case of a complex function f(z) the
path of the definite integral 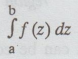 can be along any curve from z =
a to z = b. Its value depends upon the path (curve) of integration. But, the
value of integral from a to b remains the same, if the different curves from a
to b are regular curves.
can be along any curve from z =
a to z = b. Its value depends upon the path (curve) of integration. But, the
value of integral from a to b remains the same, if the different curves from a
to b are regular curves.
CAUCHY'S THEOREM Statement and Application
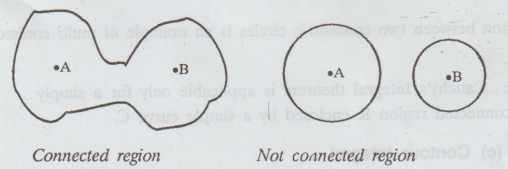
(a) Connected Region :
A
connected region is one in which any two points in it can be connected by a
curve which lies entirely within the region.
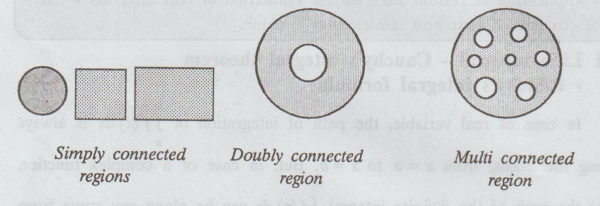
(b) Simply
connected region.
A
curve which does not cross itself is called a simple closed curve.
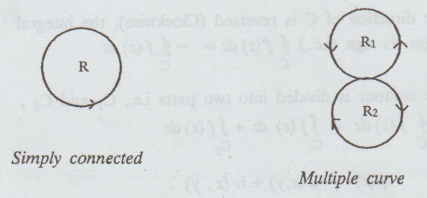
A
curve is called multiple curve, if it crosses itself.
A
region in which every closed curve in it, encloses points of the region only is
called a simply connected region.
i.e.,
A region which has no holes is called simply connected region. Otherwise, it is
said to be multiply connected.
A
multi connected region can be converted into simple connected region by taking
one or more cuts.
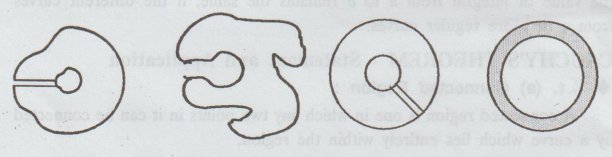
Region
between two concentric circles is an example of multi connected region.
Note (1):
Cauchy's Integral theorem is applicable only for a simply connected region R
enclosed by a simple curve C.
(c) Contour Integral
An
integral along a simple closed curve is called a contour integral.
Note (2):
In case of closed paths, the positive direction is anti-clockwise.
Note (3): If the direction of C is reversed (Clockwise), the integral changes its sign (i.e.,)
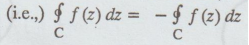
Note (4):
If the contour is divided into two parts i.e., C1 and C2,

The
evaluation of the line integral of the complex function is reduced to the
evaluation of two line integrals of real functions.
Note (5): If
C is a point on the arc joining a and b, then
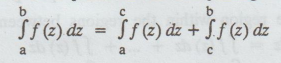
Probability and complex function: Unit IV: Complex integration : Tag: : Line integral, Cauchy's integral theorem - Complex integration
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
