Condition for Maximum Torque

Condition for Maximum Torque

From the torque equation, it is clear that torque depends on slip at which motor is running. The supply voltage to the motor is usually rated and constant and there exists a fixed ratio between E₁ and E₂. Hence E₂ is also constant. Similarly R₂, X₂ and n_s are constants for the induction motor.

Hence while finding the condition for maximum torque, remember that the only parameter which controls the torque is slip s.

Mathematically for the maximum torque we can write,

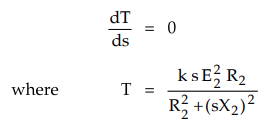
While carrying out differentiation remember that E₂, R₂, X₂ and k are constants. The only variable is slip s. As load on motor changes, its speed changes and hence slip changes. This slip decides the torque produced corresponding to the load demand.

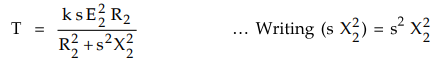
As both numerator and denominator contains s terms, differentiate T with respect to s using the rule of differentiation for u/v.

This is the slip at which the torque is maximum and is denoted as sm.

S_m = R₂ / X₂

It is the ratio of standstill per phase values of resistance and reactance of rotor, when the torque produced by the induction motor is at its maximum.

1. Magnitude of Maximum Torque

This can be obtained by substituting S_m = R₂ / X₂ in the torque equation. It is denoted by

From the expression of T_m, it can be observed that

1. It is inversely proportional to the rotor reactance.

2. It is directly proportional to the square of the rotor induced e.m.f. at standstill.

3. The most interesting observation is, the maximum torque is not dependent on the rotor resistance R₂. But the slip at which it occurs i.e. speed at which it occurs depends on the value of rotor resistance R₂.

Example 5.10.1 A 400 V, 4 pole, 3 phase, 50 Hz star connected induction motor has a rotor resistance and reactance per phase equal to 0.01 Ω and 0.1 Ω respectively. Determine i) starting torque ii) slip at which maximum torque will occur iii) speed at which maximum torque will occur iv) maximum torque v) full load torque if full load slip is 4 %. Assume ratio of stator to rotor turns as 4.

Solution : The given values are,

ii) Slip at which maximum torque occurs is,

iii) Speed at which maximum torque occurs is speed corresponding to sm,

N = N_s (1 - s_m)  = 1500 (1 - 0.1) - 1350 r.p.m.

iv) The maximum torque is,

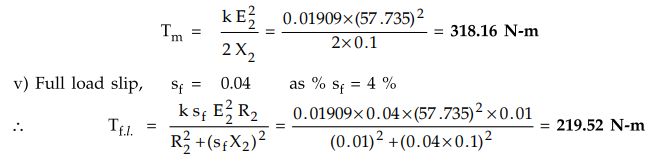
Example 5.10.2 A three phase, 50 Hz, 400 V induction motor has 4 poles star connected stator winding. Rotor resistance and reactance per phase are 0.15 Ω and 1 Ω respectively. Full load slip is 5 %. Calculate : a) Total torque developed b) Maximum torque c) Speed at maximum torque. Assume stator to rotor ratio 2:1.

Solution : The given values are,

Examples for Practice

Example 5.10.3 A 3-phase induction motor has a 4r-pole, star connected stator winding. The motor runs on a 50 Hz supply with 200 V between lines. The rotor resistance and standstill rotor reactance per phase are 0.1 Q and 0.9 Q respectively. The ratio of rotor to stator turns in 0.67. Calculate :

i) Total torque at 4 % slip

ii) Maximum torque developed

iii) Speed at maximum torque  

iv) Maximum mechanical power

Neglect stator impedance.

[Ans.: i) 40.4786 Nm, ii) 63.5065 Nm, iii) 1333.333 r.p.m., iv) 8867.1801 W] 

Example 5.10.4 Calculate the torque exerted by an 8 pole 50 Hz, 3 phase induction motor operating with a 4 % slip which develops a maximum torque of 150 kgm at a speed of 660 r.p.m. The resistance per phase of the rotor is 0.5 Ω. VTU : July-06

[Ans.: 882.9 Nm]

Example 5.10.5 A 440 V, 3ϕ, 50 Hz, 4 pole, star connected induction motor has a full load sped of 1425 rpm. The rotor has an impedance of (0.4 + j4) Ω per phase and rotor / stator turn ratio of 0.8. Calcualte : i) Full load torque; ii) Full load copper loss; iii) maximum torque and the speed at which it ocurs; iv) Starting current.

[Ans.: 78.88 Nm, 619.518 W, 98.6 Nm, 1350 r.p.m., 50.554 A]

Example 5.10.6 A 3-phase inductin motor having 6-poles, stator winding is star connected runs on 240 V, 50 Hz supply. The rotor resistance and stand still reactance are 0.12 Q and 0.85 Q per phase. The ratio of stator to rotor turns is 1.8 and full load slip is 4%. Calcualte the developed torque at full load, maximum torque and the speed at maximum torque.

[Ans.: 52.372 Nm, 99.85 Nm, 858.9 r.p.m.]

Review Question

1. Derive the condition for the maximum torque in a three phase induction motors. Also obtain the expression for the maximum torque.