Conditional Probability

CONDITIONAL PROBABILITY

1. Marginal probability

A probability of only one event that takes place is called a marginal probability.

 

2. Joint probability

The probability of occurence of both events A and B together, denoted by P (AB), is known as joint probability of A and B.

 

3. Conditional probability

The conditional probability of A given B is

P (A/B) = P (A ∩ B) / P (B) if P (B) ≠ 0 and it is undefined otherwise.

A rearrangement of the above definition yields the following:

MR (Multiplication Rule).

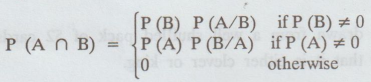
Note :

P (A/B) means the conditional probability of A given B.

P (B/A) means the conditional probability of B given A.

 

4. Conditional probability of a sample point S (an element of S)

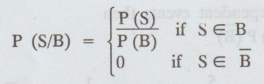
Example: When a fair dice is tossed, the conditional probability of getting '2', given that an even number has been obtained, is equal to 1/3

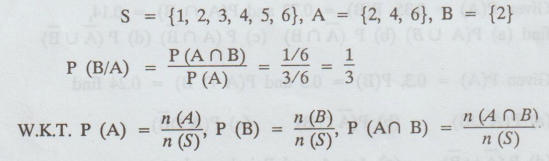
Note :

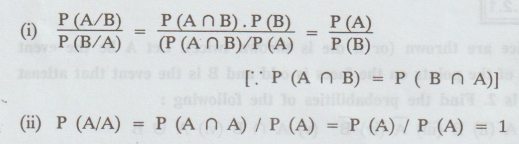
(iii) If A and B are independent events then P (A ∩ B) = P(A) P (B)

The conditional probability can be defined as follows:

 

5. Relationship between conditional, joint and marginal probabilities.

We know that the conditional probability of event B given that A has already happened is given by

P (B/A) = P(A ∩ B) / P(A), where P (A ∩ B) is the joint probability of events A and B happening together and P (A), the marginal probability of the happening of event A.

 

6. Theorem :

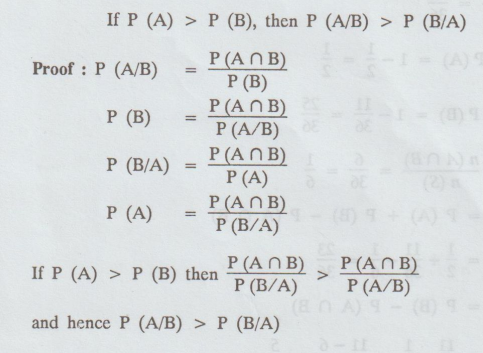
Example 1.2.1

When two dice are thrown (or a die is thrown twice). Let A be the event that the sum of the points on the faces is odd and B is the event that atleast one number is 2. Find the probabilities of the following:

 

Example 1.2.2

Among the workers in a factory only 30% receive a bonus. Among those receiving the bonus only 20% are skilled. What is the probability of a randomly selected worker who is skilled and receiving bonus.

Solution: A = {The event of receiving bonus}

B = {The event of considering skilled workers}

Given: P (A) = 30 / 100 = 0.3

P (B/A) = 20 / 100 = 0.2

P (B/A) = P(B ∩ A) / P(A)

To find the probability of the event A ∩ B

(i.e.,) P (A ∩ B) = P (A) P (B/A)

= (0.3) (0.2) = 0.06

P (B/A) → The conditional probability of event B when the event

A has already happened.

 

Example 1.2.3

Two manufacturing plants produce similar parts. Plant I produces 1,000 parts, 100 of which are defective. Plant II produces 2,000 parts, 150 of which are defective. A part is selected at random and found to be defective. What is the probability that it come from plant I.

Solution :

A - → the part selected come from plant I (A)

B -→ the part selected is defective.

A ∩ B - → the part selected is defective and came from plant I

A/B - → The conditional probability of event A when the event B has already happened.

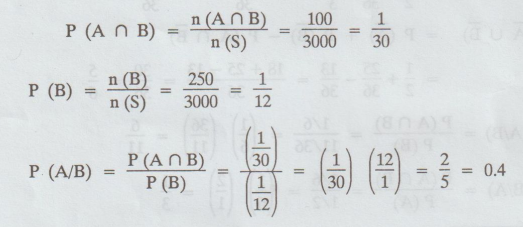
Example 1.2.4

A bag contains 5 red and 3 green balls and a second bag 4 red and 5 green balls. One of the bages is selected at random and a draw of 2 balls is made from it. What is the probability that one of them is red and the other is green.

Solution :

Let A₁ and A₂ denote the event of selecting the first bag and second bag respectively.

P(A₁) = 1/2 = P(A₂) and A₁ and A₂ are mutually exclusive events.

Sample S = A₁ ∪ A₂

Let B denote the event of selecting one red and one green ball. Then

 

Example 1.2.5

Find the probability of drawing two red balls in succession from a bag containing 3 red and 6 black balls when (i) the ball that is drawn first is replaced (ii) it is not replaced.

Solution :

Let A = {the event that the ball drawn is red}

B = {the event that the second ball drawn is red}

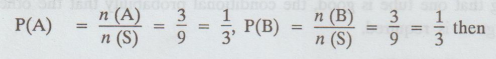
 (i) If the first ball drawn is replaced, the events are independent

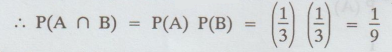
 (ii) If the first ball is not replaced after taking a red ball the bag will contain only 8 balls out of which 2 are red. The events are not independent

 

Example 1.2.6

A manufacturer of aeroplane parts knowns that the probability is 0.8 that an order will be ready for shipment on time, and it is 0.7 that an order will be ready for shipment and will be delivered on time. What is the probability that such an order will be delivered on time given that it was also ready for shipment on time?

Solution: Let 'A' be an event that an order is ready for shipment on time.

Let 'D' be an event that an order is delivered on time.

Given that P (A) = 0.8 and P (A ∩ D) = 0.7

To find P (D/A)

P (D/A) = P(A ∩ D) / P(A) = 0.7 / 0.8 = 7/8 = 0.875.

 

Example 1.2.7

A box contains 4 bad and 6 good tubes. Two are drawn out from the box at a time. One of them is tested and found to be good. What is the probability that the other one is also good? [A.U M/J 2007]

Solution:

Let A = one of the tubes drawn is good

B = the other tube is good

P (A ∩ B) = P [both the tubes drawn are good]

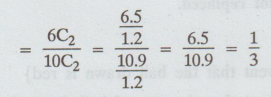
Knowing that one tube is good, the conditional probability that the other tube is also good is required.

 

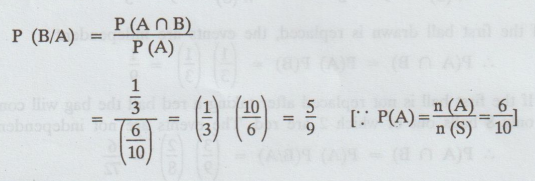
Example 1.2.8

If the probability that a communication system will have high fidelity is 0.81 and the probability that it will have high fidelity and high selectivity is 0.18, what is the probability that a system with high fidelity will also have high selectivity? [A.U N/D 2007]

Solution:

A = The event that a communication system has high selectivity.

B = The event that it has high fidelity

Given: P(B) = 0.81, P(A ∩ B) = 0.18

P(A/B) = P(A ∩ B) / P(B) = 0.18 / 0.81 = 18/81 = 2/9

 

Example 1.2.9

In a certain group of computer personnel, 65% have insufficient knowledge of hardware, 45% have inadequate idea of software and 70% are in either one or both of the two categories. What is the percentage of people who know software among those who have a sufficient knowledge of hardware? [A.U N/D 2006]

Solution: Let

P (A) = Probability of people having insufficient knowledge of hardware

= 65% = 65 / 100 = 0.65

The percentage of people who know software among those who have a sufficient knowledge of hardware is 85.7.

 

Example 1.2.10

Given a binary communication channel, where A is the input and B is the output, let P (A) = 0.4, P (B/A) = 0.9 and 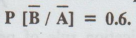 = 0.6. Find (1) P (A/B),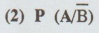 

Solution :