Probability and complex function: Unit III: Analytic functions
Construction of analytic function
There are three methods to find f (z).
CONSTRUCTION
OF ANALYTIC FUNCTION
There
are three methods to find f (z).
Method 1.
Exact differential method.
(i)
Suppose the harmonic function u (x, y) is given.
Now,
dv = vx dx + vy dy is an exact differential
where
vx and vy are known from u by using C-R equations.

(ii)
Suppose the harmonic function v (x, y) is given
Now,
du = ux dx+uy dy is an exact differential
where
ux and uy are known from v by using C-R equations
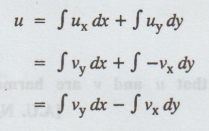
Method 2.
Substitution method
f(z)
= 2u [ ½ ( z + a), -i/2 (z - a) ] – [ u(a,0), -iv(a,0)]
Here,
u (a, 0) — iv (a, 0) is a constant
Thus
f(z) = 2u [1/2 (z + a), -i/2(z - a)] + C
By
taking a = 0, that is, if f (z) is analytic at z = 0 + i0,
we
have the simpler formula for f (z)
f(z)
= 2 [u(z/2 , -iz/2)] + C
Method 3 [Milne-Thomson method]
(i)
To find f (z) when u is given
Let
f (z) = u + iv
f'
(z) = ux + ivx
=
ux - iuy [by C.R., condition]
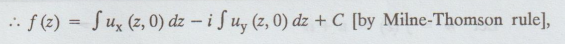
where
C is a complex constant.
(ii)
To find f (z) when v is given
Let
f (z) = = u + iv
f'
(z) = ux + ivx
=
vy + i vx [by C.R., condition]
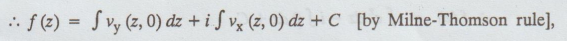
where
C is a complex constant.
Probability and complex function: Unit III: Analytic functions : Tag: : - Construction of analytic function
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
