Construction of the Circle Diagram

Construction of the Circle Diagram  AU : May-07, 14, 16, 17, Nov.-04, Dec.-04, 05, 13

By using the data obtained from the no load test and the blocked rotor test, the circle diagram can be drawn using the following steps :

Step 1 : Take reference phasor V as vertical (Y-axis).

Step 2 : Select suitable current scale such that diameter of circle is about 20 to 30 cm. 

Step 3 : From no load test, I_o and ϕ_o are obtained. Draw vector I_o, lagging V by angle ϕ_o. This is line ∞ ' as shown in the Fig. 6.5.1.

Step 4 : Draw horizontal line through extremity of I_o i.e. O', parallel to horizontal axis.

Step 5 : Draw the current ISN calculated from Isc with the same scale, lagging V by angle ϕ_sc, from the origin O. This is phasor OA as shown in the Fig. 6.5.1.

Step 6 : Join O'A. the line O'A is called Output line.

Step 7 : Draw a perpendicular bisector of O'A. Extend it to meet line OT5 at point C. This is the centre of the circle.

Step 8 : Draw the circle, with C as a centre and radius equal to O'C. This meets the horizontal line drawn from O' at B as shown in the Fig. 6.5.1.

Step 9 : Draw the perpendicular from point A on the horizontal axis, to meet OT5 line at F and meet horizontal axis at D.

Step 10 : Torque line

The torque line separates stator and rotor copper losses.

Note that as voltage axis is vertical, all the vertical distances are proportional to active components of currents or power inputs, if measured at appropriate scale.

Thus the vertical distance AD represents power input at short circuit i.e. WSN, which consists of core loss and stator, rotor copper losses.

Now FD = O’G = fixed loss

where O'G is drawn perpendicular from O' on horizontal axis. This represents power input on no load i.e. fixed loss.

Hence AF ∝ sum of stator and rotor copper losses

Then point E can be located as,

AE / EF = rotor copper loss / stator copper loss

The line OTi under this condition is called torque line.

Power scale : As AD represents W_SN i.e. power input on short circuit at normal voltage, the power scale can be obtained as,

Power scale = W_SN / l(AD) W/cm

where l(AD) - Distance AD in cm

Location of Point E : In a slip ring induction motor, the stator resistance per phase R₁ and rotor resistance per phase R₂ can be easily measured. Similarly by introducing ammeters in stator and rotor circuit, the currents I₁ and I₂ also can be measured.

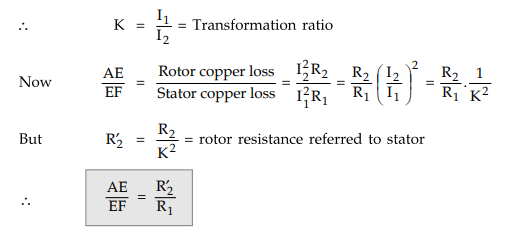
Thus point E can be obtained by dividing line AF in the ratio R2 to Rr

In a squirrel cage motor, the stator resistance can be measured by conducting resistance test.

Stator copper loss = 3 I²_SN R₁ where I _SN is phase value

Neglecting core loss, W_SN = Stator Cu loss + Rotor Cu loss

Rotor copper loss = W_SN - 3 I²_SN  R1

Dividing line AF in this ratio, the point E can be obtained and hence OT! represents torque line.

1. Predicting Performance from Circle Diagram

Let motor is running by taking a current OP as shown in the Fig. 6.5.1. The various performance parameters can be obtained from the circle diagram at that load condition.

Draw perpendicular from point P to meet output line at Q, torque line at R, the base line at S and horizontal axis at T. 

We know the power scale as obtained earlier.

Using the power scale and various distances, the values of the performance

parameters can be obtained as,        

1. Total motor input = PT × Power scale

2. Fixed loss = ST × Power scale

3. Stator copper los = SR × Power scale

4. Rotor copper loss = QR × Power scale

5. Total loss  = QT × Power scale

6. Rotor output = PQ × Power scale

7. Rotor input = PQ + QR = PR × Power scale

8. Slip s = Rotor Cu loss / Rotor input = QR / PR

9. Power factor cos ϕ =  PT / OP

10. Motor efficiency =   Output / Input = PQ / PT

11. Rotor efficiency = Rotor output / Rotor input = PQ / PR

12. Rotor output / Rotor input         = 1 - s = N/Ns = PQ / PR

The torque is the rotor input in synchronous watts.

2. Maximum Quantities

The maximum values of various parameters can also be obtained by using circle diagram.

1. Maximum Output : Draw a line parallel to O'A and is also tangent to the circle at point M. The point M can also be obtained by extending the perpendicular drawn from C on OA. to meet the circle at M. Then the maximum output is given by Z(MN) at the power scale. This is shown in the Fig. 6.5.1.

2. Maximum Input : It occurs at the highest point on the circle i.e. at point L. At this point, tangent to the circle is horizontal. The maximum input is given Z(LL') at the power scale. 

3. Maximum Torque : Draw a line parallel to the torque line and is also tangent to the circle at point J. The point J can also be obtained by drawing perpendicular from C on torque line and extending it to meet circle at point J. The Z(JK) represents maximum torque in synchronous watts at the power scale. This torque is also called stalling torque or pull out torque.

4. Maximum Power Factor : Draw a line tangent to the circle from the origin O, meeting circle at point H. Draw a perpendicular from H on horizontal axis till it meets it at point I. Then angle OHI gives angle corresponding to maximum power factor angle.

Maximum p.f. = cos [∠ OHI] = HI / OH

5. Starting Torque : The torque is proportional to the rotor input. At s = 1, rotor input is equal to rotor copper loss i.e. l(AE).

Tstart = l(AE) × Power scale … In synchronous watts

3. Full Load Condition

The full load motor output given on the name plates in watts or h.p. Calculate the distance corresponding to the full load output using the power scale.

Then extend AD upwards from A onwards, equal to the distance corresponding to full load output, say ADraw parallel to the output line O'A from A' to meet the circle at point P'. This is the point corresponding to the full load condition, as shown in the Fig. 6.5.2.

Once point P' is known, the other performance parameters can be obtained easily as discussed above.

Example 6.5.1 A 415 V, 29.84 kW, 50 Hz delta connected motor gave the following test data :

No load test : 415 V, 21 A, 1250 W. Locked rotor test : 100 V, 45 A, 2730 W. Construct the circle diagram and determine the line current and power factor for rated output, and the maximum torque. Assume stator and rotor Cu losses equal at stand still. AU : May-07, Marks 12 

Solution : From no load test,

Choose current scale to be 1 cm = 10 A

1) Draw vector OO = I_o = 21 A i.e. 2.1 cm with ϕ_o = 85.25° measured from voltage axis i.e. Y-axis.

2) Draw horizontal line from O' parallel to X-axis.

3) Draw vector OA = I_SN - 186.75 A , i.e.18.67 cm at ϕ_SC = 69.49° from voltage axis.

4) Join O'A, this is output line.

5) Draw perpendicular bisector of O'A to meet the horizontal line drawn from O' at C. This is centre of the circle.

6) With C as a centre and CO' as radius, draw a semicircle to meet horizontal line from O' at B, as shown in the Fig. 6.5.3.

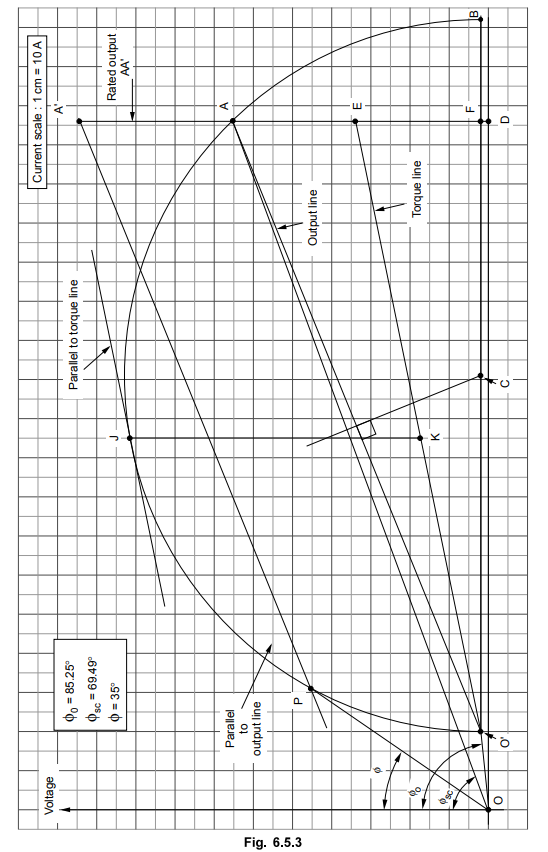
7) Draw perpendicular from A on X-axis to meet at point D.

8) As the stator and rotor copper losses are equal, E point is midpoint of AF i.e. AE = AF.

Join CTE, this is torque line.

9) To locate full load point, draw AA' such that

10) Draw the parallel line to the output line from O' to meet the circle at P. This is full load point for rated output.

l(OP) = rated line current = 5.7 cm from graph

= 57 A (phase value as delta connected)

I_L = √3×57 = 98.7268 A

ϕ = 35°

cos ϕ = rated power factor = 0.819 lagging

For maximum torque, draw parallel to torque line and tangent to the circle at J. Draw

JK vertical till torque line.

l(J K) = 7.5 cm = Maximum torque in syn. watts

At the power scale,

T_max = 7.5 × 7289.45 = 54670.87 syn. watts

Example 6.5.2 A 4.5 kW, 400 V, 50 Hz, 3 phase delta connected induction motor gave the following test results.

No load : 400 V, 4.2 A, 480 W

Blocked rotor test : 215 V, 15 A, 1080 W

The ratio of stator to rotor resistance referred to stator is 2 : 1. Calculate the torque, line current, power factor and efficiency at 125 % of full load.

Solution :

From no load test,

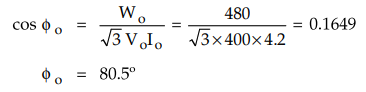
From blocked rotor test,

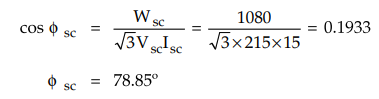
As motor is delta connected, per phase current is 1/ √3 times line value.

Choose current scale 1 cm = 1 A

I_o(phase) = 4.2 / √3  = 2.424 A = 2.424 cm

Draw the circle diagram by usual method as shown in the Fig. 6.5.4

From circle diagram, l(AD) = 3.55 cm = W_SN

Hence point E is between A and F such that,

Stator copper loss / Rotor copper loss = EF / AE  = R₁ / R₂ = 2/1

From circle diagram, Z(AF) = 3.25 cm

AF = AE + EF = AE + 2 AE

AE = 'AF / 3 = 1.0833 cm, EF = 2.166 cm

For 125 % of full load :

1.25xFullloadoutput = 1.25 × 4.5 = 5.625 kW

As per power scale, locate A' above A at a distance,

AA’ = 5.625 × 10³ / 1053 . 024 = 5.3417 cm

Draw a line parallel to ouput line till it intersects the circle at P. Draw vertical line from P to intersect output line at Q, torque line at R, base line at S and X-axis at T.

From circle diagram, as shown in the Fig. 6.5.4.

l(PQ) = 5.35 cm, l(QR) = 0.3 cm, l (RS) = 0.58 cm, l (PT) = 6.55 cm, l (OP) = 8.85 cm

i) Line current = √3 ×  l(OP) × Current scale = 15.3286 A

ii) cos ϕ = cos(41°) = 0.7547 lagging

iii) % ƞ = Output / Input × 100 = pQ / PT × 100 = 5.35 / 6.55 × 100 = 81.68 %

Example 6.5.3 The following data refers to a 10-pole, 400 V, 50 Hz, 3 phase induction motor :

R₁ = 1.75 Ω, X₁ =5.5 Ω, R₂ = 2.25 Ω, X₂ = 6.6 Ω. When the motor is tested on no-load, it is observed that it takes 3.8 A (line current) and the total core loss is 310 W. By using an approximate equivalent circuit at 4% slip, calculate :

- the rotor current - supply current and power factor

- mechanical power developed - gross load torque Also determine the equivalent circuit.

Solution :

I₀ = 3.8 A, s = 4%, W_o = 310 W, P = 10, V_L = 400 V

Assuming star connection,

Example 6.5.4 A 3-phase, 4-pole, 60 kW, 50 Hz induction motor connected to rated supply voltage and running without additional load consumes 3 kW. When prevented from rotating it draws rated current at 30 % rated supply and takes a power input of 4 kW. Assuming that under rated load conditions, The stator and rotor copper losses are equal and that the mechanical losses are 30 % of the no-load losses, determine slip, at rated load.

Solution :  

P_NL = No load input = 3 kW

P_BL = Power input when rotor blocked = 4 kW

Mechanical loss = 30 % PNL = 0.3 × 3 = 0.9 kW

On no load, input current is very small hence stator copper loss is negligible.

P_NL = Stator iron loss + Mechanical loss

Stator iron loss = 3 × 10³ -0.9 × 10³ = 2100 W = 2.1 kW = P_i 

When rotor is blocked and prevented from rotating,

V_BL = 30 % of V = 0.3 V

(Stator iron loss = P_i ) ∝ V

P_{i BL} = Stator iron loss for rotor blocked = 630 W

P_BL = P_iBL + Stator copper loss + Rotor copper loss

But at rated load current, Stator cu loss = Rotor cu loss (given)

4 × 10³ = 630 + 2 stator cu loss

Stator cu loss = 1685 W

P_c = Rotor cu loss = 1685 W

P_m = P_out + Mechanical loss  … P_out = 60 kW

P_m = 60 × 10³ + 0.9 × 10³ = 60.9 kW

Now P₂ : P_c : P_m is 1 : s : 1 – s

P_c / P_m = s / 1 – s i.e. 1685 / 60 × 10³ = s / 1 - s

 s = 0.027 i.e. 2.7 % … At full load

Example 6.5.5 A 10 kW, 420 V, 3-phase, 4-pole, 50 Hz delta  connected squirrel cage induction motor gave the following data on blocked rotor test : 210 V, 20 A, 5 kW stator core loss at rated voltage and frequency is 300 walts. The d.c. resistance measured between any two terminals of stator is 0.6 ohm. Determine the starting torque.

Solution :

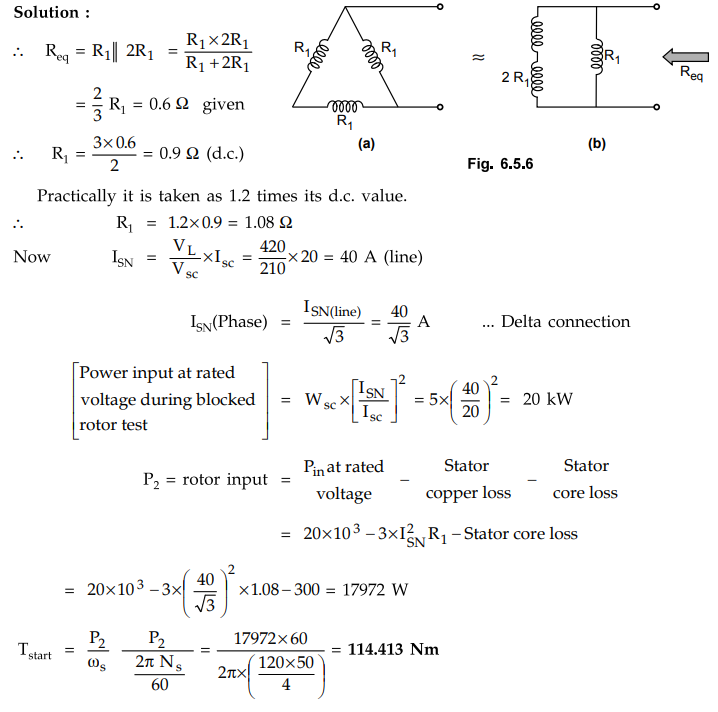
Example 6.5.6 Draw the circle diagram of a 15 hp, 230 V, 50 Hz, 3-phase slip-ring induction motor with a star connected stator and rotor. The winding ratio is unity. The stator resistance is 0.42 Ω/ptose and the rotor resistance is 0.3 Ω/phase. The following are the test readings,

No load test : 230 V, 9 A, p.f. = 0.2143

Blocked rotor test : 115 V, 45 A, p.f. = 0.454

Find : i) Starting torque ii) Maximum torque iii) Maximum power factor iv) Slip for maximum torque v) Maximum power output.

Solution :

From no load test, cos ϕ₀ = 0.2143, 0 = 77.62°

From blocked rotor test, cos ϕ_sc = 0.454, ϕ_sc = 63°

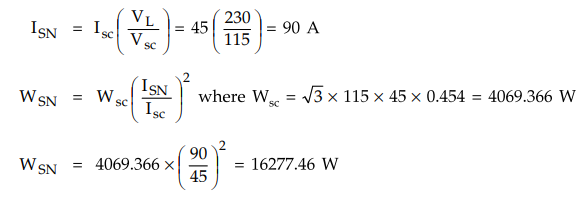
Choose the current scale to be 1 cm = 7 A

1. Draw OO' - Io = 9 A i.e. 1.28 cm at ϕ₀ 77.62° from Y-axis.

2. Draw O’A - I_SN - 90 A i.e. 12.85 cm at ϕ_sc = 63° from Y-axis.

3. Join O'A, which is output line.

4. Draw perpendicular bisector of O'A to meet horizontal line from O' at C. This is the centre of the circle.

5. Draw circle with radius O'C and C as a centre to meet horizontal line from O' at B, as shown in the Fig. 6.5.7.

6. Draw perpendicular from A on X-axis, at point D.

l(AD) = 5.95 cm = W_SN

Power scale = W_SN / l(AD) = 16277. 46 / 5.95 = 2735.707 W/cm

7. To locate point E, use the relation

AE = 0.4167 AF and from graph l(AF) = 5.7 cm

AE = 2.37 cm, EF - 3.33 cm

8. Join O’E which is torque line.

i) Starting torque = AE = 2.37 cm i.e. 2.37 × 2735.707

= 6483.62 syn-watts

ii) For maximum torque, draw line parallel to the torque line (OT) which is tangent to circle at J. Draw a vertical line from J to meet torque line at K.

l (JK) = T_m = 4.8 cm = 4.8 × 2735.707 = 13131.39 syn-watts

iii) Draw a line tangent to the circle from O, meeting circle at H. The angle made by OH with Y axis is (|> m and maximum power factor is cos ϕ_m.

m = 31° hence maximum p.f. = cos ϕ_m = 0.857 lagging

iv) Slip for maximum torque = LK / JK = 1.1 / 4.8 = 0.229 i.e. 22.91%

v) Extend perpendicular bisector of O'A to meet the circle at M. Draw vertical from M to meet the output line at N then Z(MN) = Maximum output.

Maximum output = l(MN) = 3.9 cm

= 3.9 × 2735.707 = 10.6692 kW 

Example 6.5.7 A 15 kW, 400 V, 50 Hz, 3 phase star connected induction motor gave the following test results :

No load test : 400 V, 9 A, 1310 W

Blocked rotor test : 200 V, 50 A, 7100 W

Stator and rotor ohmic losses at standstill are assumed equal.

Draw the induction motor circle diagram and calculate

i) Line current ii) Power factor iii) Slip iv) Torque and efficiency at full load AU : May-14, Marks 16

Solution :

From no load test,

Choose the current scale to be 1 cm = 5 A.

1. Draw vector OO' = I_o = 9 A i.e. 1.8 cm at ϕ_o = 77.47° from voltage axis.

2. Draw horizontal line from O' parallel to X-axis.

3. Draw vector OA = I_SN = 100 A i.e. 20 cm at ϕ_sc = 65.80° from voltage axis.

4. Join O'A. This is output line.

5. Draw perpendicular bisector O'A to meet horizontal line drawn from O' at C. This is the centre of the circle. 

6. With C as centre and CO' as radius, draw a semicircle to meet horizontal line from O' at B.

7. Draw perpendicular from A on X-axis, meeting at point D.

l(AD) = 8.2 cm = W_SN

Power scale = W_SN / l(AD) = 28400 / 8.2 = 3463.41 W/cm

8. As the stator and rotor ohmic losses are equal, point E is mid-point of AF i.e. AE = AF.

Join OTi. This is the torque line.

9. To locate full load point, draw AA' such that

AA’ = 15 kW = 15000 W

= 15000 / 3463.41 = 4.33 cm

10. Draw parallel to the output line from A' to meet circle at point P. This is the full load point.

11. Draw vertical line from P to intersect output line at Q, torque line at R, base line at S and X-axis at T.

So at full load,

Examples for Practice

Example 6.5.8 A 5-kW, 220 V, 50-Hz, 6-pole, 3-phase, star-connected induction motor gave the following test data :

No-load test : 220 V, 6 A, 475 W (Line values)

Blocked rotor test : 110 V, 27 A, 1930 W.

Determine from circle diagram for full load condition the line current, p.f, torque, slip and efficiency. Also determine maximum output, maximum torque and slip for maximum torque. Take stator cu. loss at stand still twice the rotor cu. loss.

[Ans.: i) 18 A, ii) 0.88 lagging, iii) 5121.1878 syn-watts, iv) 7.46 %, v) 82.05 %, vi) 6955.64 W, vii) 7796.435 Syn-Watts, viii) 14.7 %]

Example 6.5.9 Draw the circle diagram for a 5.5 kW, 400 V, 3-phase, 50 Hz, 4-pole slip ring induction motor from the test data given below (line values) :

No load test: 400 V, 6 A, 0.085 p.f. lag

Blocked rotor test : 100 V, 12 A, 700 W

The ratio of primary to secondary turns is 2.6, stator resistance per phase is 0.67 Q and that of rotor is 0.18 Ω. Calculate,

i) Full load current

ii) Full load slip

iii) Ratio of maximum torque to full load torque iv) Starting torque.

[Ans.: i) 13.5 A, ii) 6.8 %, iii) 1.965, iv) 44.96 N-m]

Example 6.5.10 Draw the circle diagram for a 20 HP, 50 Hz, 3 phase, star connected induction motor with the following data.

No load test : 400 V, 9 A, 0.2 p.f. lagging

Blocked rotor test : 200 V, 50 A, 0.4 p.f. lagging

Determine the line current and efficiency for full load condition from the circle diagram.        

[Ans.: 30 A (0.866 lag), 80.75 %]

Example 6.5.11 Draw the circle diagram from no load and short circuit test of a 3-phase, 14.92 kW, 400 V, 6 pole induction motor with the following test data (line values).

No load : 400 V, 11 A, p.f. = 0.2

S.C. Test : 100 V, 25 A, p.f. = 0.4

Rotor copper loss at standstill is half the total copper loss. From the diagram, find

i) Line current ii) Slip iii) Efficiency iv) p.f. at full load and v) Maximum torque.

[Ans.: 32.75 A, 6.5 %, 80.73 %, 0.83 log, 26673.57 synchronous watts] 

Example 6.5.12 A 415 V, 29.84 kW, 50 Hz, delta connected motor gave the following test data.

No-load test : 415 V, 21 A, 1250 W

Blocked rotor test :         100 V, 45 A, 2730 W

Construct the circle diagram and determine i) Line current and power factor for rated output ii) The maximum torque. Assume stator and rotor copper losses are equal at standstill.

[Ans. : 59.44 A, 0.819 lagging, 52595.93 syn-watts]

Review Questions

1. Explain the procedure of drawing circle diagram of an induction motor. What information can be drawn from the circle diagram and how ?

2. How the performance of an induction motor is predicted at a given load, using a circle diagram ?

3. How the various maximum quantities can be obtained from a circle diagram ?

4. How full load point can be located on a circle diagram ?