Contour Integral

(c) Contour Integral

An integral along a simple closed curve is called a contour integral.

Note (2): In case of closed paths, the positive direction is anti-clockwise.

Note (3): If the direction of C is reversed (Clockwise), the integral changes its sign (i.e.,) 

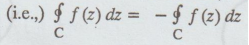
Note (4): If the contour is divided into two parts i.e., C1 and C2, then

The evaluation of the line integral of the complex function is reduced to the evaluation of two line integrals of real functions.

Note (5): If C is a point on the arc joining a and b, then

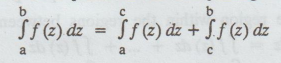
I. Cauchy's Integral theorem (or) Cauchy's Theorem (or) Cauchy's Fundamental theorem 

[A.U N/D 2016 R-13] [Anna, May 2002]

State and prove Cauchy's integral theorem.

Statement: If a function f(z) is analytic and its derivative f' (z) is continuous at all points inside and on a simple closed curve C, then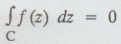 

Proof: Let the domain enclosed by C be denoted by R.

Let f (z) = u (x,y) + iv (x,y)

z= x + iy; dz = dx + idy

Since, f' (z) is continuous, the four partial derivatives ∂u/ ∂x, ∂u/ ∂y , ∂v/ ∂x and ∂v/ ∂y are also continuous in R and C.

Hence, we can apply Green's theorem for a plane.

II. Cauchy's theorem for multiply connected Region.

If f (z) is analytic in the doubly connected regio. R bounded by two simple closed curves C₁ and C₂, then

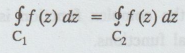
If there are finite number of simple closed curves C₁, C₂, ... C_n inside C and f (z) is analytic in the region within the regions between the curves C₁, C₂....C_n, then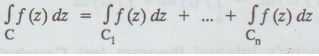 

III. Cauchy's Integral formula

State and prove Cauchy's integral formula. [Anna, Nov 1996]

Statement: If f (z) is analytic inside and on a closed curve C of a simply connected region R and if 'a' is any point within C, then

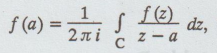 the integration around C being taken in the positive direction.

Proof: Since, f (z) is analytic inside and on C.

f(z) /z – a is also analytic inside and on C, except at the point z = a.

Hence, we draw a small circle y with centre at z = a and radius p lying entirely inside C.

Now, f(z) /z – a is analytic in the region enclosed between C and y.

Hence, by Cauchy's extended theorem.

IV. Cauchy's Integral formula for derivative.

Statement: If a function f (z) is analytic within and on a simple closed curve C and 'a' is any point lying in it, then 

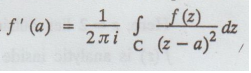
Proof: Cauchy's integral formula is