Conversion of Numbers from One Radix to Another Radix

Conversion of Numbers from One Radix to Another Radix

AU May-08,10,11,12,13,15, Dec.-11

 

1. Binary to Octal Conversion

• The base for octal number is 8 and the base for binary number is 2.

• The base for octal number is the third power of the base for binary numbers. Therefore, by grouping 3 digits of binary numbers and then converting each group digit to its octal equivalent we can convert binary number to its octal equivalent.

 

Ex. 1.3.1 Convert 10101101.0111 to octal equivalent.

Sol. :

Step 1 : Make group of 3-bits starting from LSB for integer part and MSB for fractional part, by adding Os at the end, if required.

Step 2 : Write equivalent octal number for each group of 3-bits.

 

2. Octal to Binary Conversion

• Conversion from octal to binary is a reversal of the process explained in the previous section. Each digit of the octal number is individually converted to its binary equivalent to get octal to binary conversion of the number.

 

Ex. 1.3.2 Convert (12562 )8 to binary.

Sol. :

Step 1 : Write equivalent 3-bit binary number for each octal digit.

Step 2 : Remove any leading or trailing zeros.

 

3. Binary to Hexadecimal Conversion

• The base for hexadecimal numbers is 16 and the base for binary numbers is 2.

• The base for hexadecimal number is the fourth power of the base for binary numbers. Therefore, by grouping 4 digits of binary numbers and then converting each group digit to its hexadecimal equivalent we can convert binary number to its hexadecimal equivalent.

 

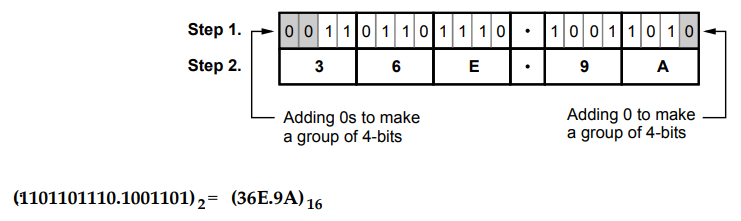
Ex. 1.3.3 Convert 1101101110 . 1001101 to hexadecimal equivalent.

Sol. :

Step 1 : Make group of 4-bits starting from LSB for integer part and MSB for fractional part, by adding Os at the end, if required.

Step 2 : Write equivalent hexadecimal number for each group of 4-bits.

 

4. Hexadecimal to Binary Conversion

• Conversion from hexadecimal to binary is a reversal of the process explained in the previous section. Each digit of the hexadecimal number is individually converted to its binary equivalent to get hexadecimal to binary conversion of the number.

 

Ex. 1.3.4 Convert (549. B4)16 to binary.

Sol. :

AU : May-15, Mark 1

Step 1 : Write equivalent 4-bit binary number of each hexadecimal digit.

Step 2 : Remove any leading or trailing zeros.

 

5. Octal to Hexadecimal Conversion

The easiest way to convert octal number to hexadecimal number is given below.

1. Convert octal number to its binary equivalent.

2. Convert binary number to its hexadecimal equivalent.

 

Ex. 1.3.5 Convert (615.25)s to its hexadecimal equivalent.

Sol. :

Step 1 : Write equivalent 3-bit binary number for each octal digit.

Step 2 : Make group of 4-bits starting from LSB for integer part and MSB for fractional part by adding Os at the end, if required.

Step 3 : Write equivalent octal number for each group to 4-bits.

 

6. Hexadecimal to Octal Conversion

• The easiest way to convert hexadecimal number to octal number is given below.

1. Convert hexadecimal number to its binary equivalent.

2. Convert binary number to its octal equivalent.

 

Ex. 1.3.6 Convert (BC66.AF)₁₆ to its octal equivalent.

Sol. :

Step 1 : Write equivalent 4-bit binary number for each hexadecimal digit.

Step 2 : Make group of 3-bits starting from LSB for integer part and MSB for fractional part by adding Os at the end, if required.

Step 3 : Write equivalent octal number for each group of 3-bits.

 

7. Converting Any Radix to Decimal

• In general, numbers can be represented as

where N = Number in decimal

A = Digit

r = Radix or base of a number system

n = The number of digits in the integer portion of         number

m = The number of digits in the fractional portion of number

• From this general equation we can convert number with any radix into its decimal equivalent. This is illustrated using following example.

 

Ex. 1.3.7 Convert (3102.12)₄ to its decimal equivalent. 

Sol. : N = 3 × 4³ + l × 4² + 0 × 4¹ + 2 × 4⁰ + l × 4^-1 + 2 × 4^-2

= 192 + 16 + 0 + 2 + 0.25 + 0.125 = 210.375₁₀

 

Ex. 1.3.8 Determine the value of base x, if : (193)_x = (623)₈

Sol. : (193)_x = (623)₈

Converting octal into decimal :

 

8. Conversion of Decimal Number to Any Radix Number

Step 1 : Convert integer part.

Step 2 : Convert fractional part.

• The conversion of integer part is accomplished by successive division method and the conversion of fractional part is accomplished by successive multiplication method.

Steps in Successive Division Method

1. Divide the integer part of decimal number by desired base number, store quotient (Q) and remainder (R).

2. Consider quotient as a new decimal number and repeat step 1 until quotient becomes 0.

3. List the remainders in the reverse order.

Steps in Successive Multiplication Method

1. Multiply the fractional part of decimal number by desired base number.

2.  Record the integer part of product as carry and fractional part as new fractional part.

3. Repeat steps 1 and 2 until fractional part of product becomes 0 or until you have many digits as necessary for your application.

4. Read carries downwards to get desired base number.

 

Ex. 1.3.9 Convert 12.125 decimal into binary.

Sol. :

Integer part : Conversion of integer part by successive division method.

Fractional part : Conversion of fractional part by successive multiplication method.

 

Ex. 1.3.10 Convert 658.825 decimal into octal.

Sol. :

Integer part : Conversion of integer part by successive division method.

Fractional part : Conversion of fractional part by successive division method.

In this example, we have restricted fractional part up to 3 digits. This answer is an approximate answer. To get more accurate answer we have to continue multiplying by 8 until we have as many digits as necessary for our application.

 

Ex. 1.3.11 Convert 5386.345 decimal into hexadecimal.

Sol . :

Integer part : Conversion of integer part by successive division method.

Fractional part : Conversion of fractional part by successive multiplication method.

In this example, we have restricted fractional part up to 3 digits. This answer is an approximate answer. To get more accurate answer we have to continue multiplying by 16 until we have as many digits as necessary for our application.

 

Ex. 1.3.12 The solution to the quadratic equation x² - 11x+22=0 is x = 3 and x = 6. What is the base of the numbers ? AU CSE May-12, Marks 2

Sol. :

Given quadratic equation is x² - 11x + 22 = 0 and it is given that x = 3 and x = 6

(x − 3) (x −6) = x² - 11x + 22 ...(1)

The numbers 3 and 6 are same in any base, whose value is more than 6.

i.e., (3)_b = (3)₁₀

= (6)_b = (6)₁₀  where b base

Solving equation (1) we have,

(x² - 9x + 18)10 = (x² - 11x + 22)b

Comparing coefficients of x we have

(-9)₁₀ = (-11)_b

 (9)₁₀ = (11)_b

9 = b¹ + b⁰ = b + 1

b = 8

or comparing constants we have

(18)₁₀ = (22)_b

18 = 2b + 2

b = 8

 

Ex. 1.3.13 Determine the value of b for the following :

i) (292)₁₀ = (1204)_b ii) (16)₁₀ = (100)_b

 

Ex. 1.3.14 Convert (101101.1101)2 to decimal and hexadecimal form.

Sol. :

 

Examples for Practice

Ex. 1.3.15 Convert the following number from one base to other (65342 )₈ =( )₇

AU : CSE : May-08, Marks 2

[Ans.: (65.342)₈ = (1144.3042) ₇]

 

Ex. 1.3.16 Convert the (153.513)₁₀ to octal.

 [Ans.: (231.4065)₈]

 

Ex. 1.3.17 Perform the following code conversions :(1010.10)₁₆      → (?)₂ → (?)₂ → (?)_1o

[Ans. : (1000000010000.0001)₂, (10020.02) ₈, (4112.0625)₁₀ ]

 

Ex. 1.3.18 Convert (1947)₁₀ into its equivalent octal and hexadecimal representations.

[Ans. : (1947)₁₀ = (79B)₁₆ = (3633)₈]